5,6 Производящие функции, свойства

7. Линейные рекуррентные соотношения с постоянными коэффициентами. Теорема о решении линейных рекуррентных соотношений. Числа Фибоначчи.

Последовательность a1,a2,… называется возвратной или рекуррентной ,если выполняется соотношение (11.1)=0

Для любого n ,для некоторого r и чисел c1,c2,…ck, то есть an+r выражается через предыдущие.

11.1-рекурнтное соотношение

Утв.1 Если последовательности {an} и {bn} удовлетворяют соотношению (11.1) то сумма {an+bn} тоже удовлетворяет соотношению (11.1)

Утв.2 Если {an} удовлетворяет соотн. (11.1) , то {Can} тоже будет удовлетворять соотношению (11.1)

Утв.3 Если 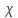(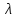) =0 , то последовательность {^n} удовлетворяет соотношению (11.1)

Утв.4 Если 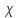(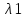) =….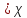(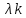) =0 и все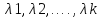различные, тоbn=C1–общее решение характеристического соотношения (11.1)

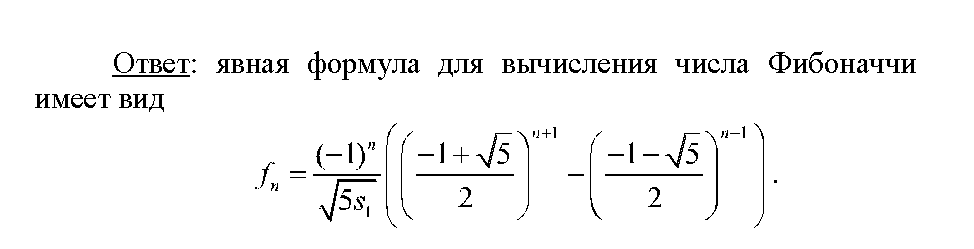
8. Булев куб. Его элементы. Функции алгебры логики. Задание функций таблицами. Элементарные функции и их свойства. Фиктивные и существенные переменные.

Булева функция (от переменных) — это произвольное отображение вида

(6.1)

т.е. булева функция определена на множестве всех n-элементных (при ) последовательностей (или n-компонентных кортежей) нулей и единиц и принимает два возможных значения: 0 и 1.

С понятием булевой функции тесно связаны понятия булевой константы и булева переменного. (В литературе по теории булевых функций традиционно употребляется термин "булева переменная" (в женском роде).)

Булева константа — это индивидная константа с областью значений . Таким образом, существуют двебулевы константы: 0 и 1. По определению принимается, что каждая булева константа есть также булева функция от 0 переменных (что вполне аналогично определению нульарной операции).

Булево переменное — это индивидное переменное с областью значений , т.е. это переменное, которое может принимать только два значения: 0 и 1 (подобно тому, как действительное переменное принимает произвольное действительное значение, а комплексное переменное — произвольное комплексное значение). Тогда с использованием понятиябулева переменного мы можем задать булеву функцию (6.1) записью , в которой каждоебулево переменное , и функция / принимают два возможных значения: 0 и 1. Переменныеназывают при этом переменнымибулевой функции . Фиксируя значениекаждого переменного, получаем кортежиз множества, называемый набором значений переменных, и соответствующее ему значение функции, которое будет значением переменного, сопоставленным заданным значениям переменных.

Подчеркнем, что, если специально не оговорено противное, в выражении все переменные предполагаются попарно различными, т.е. пробегающими каждое независимо от других множество.

Понятию булевой функции можно придать иной смысл, понимая элементы множества как истинностные значения, а именно понимая единицу как "истину", а нуль как "ложь". Такие истинностные значения могут быть, как мы знаем, сопоставлены каждому высказыванию. Тогдабулева функция есть некоторое правило, позволяющее каждому фиксированному набору истинностных значений, т.е. набору значений булевых переменных, сопоставить то или иное истинностное значение. Так может быть вычислено, например, истинностное значение сложного высказывания, составленного по определенным правилам из простых высказываний. Подобного рода сложные высказывания составляются с помощью логических операций: "или", "и", "если ..., то ..." и т.п. Указанная логическая интерпретация булевой функции позволяет понять, почему булево переменное часто называют логическим переменным (традиционный термин: "логическая переменная"), а булеву функцию — логической функцией (или функцией алгебры логики).

Кроме того, согласно определению, булева функция от переменных есть отображение n-й декартовой степени множествав множество, т.е. не что иное, как n-арная операция на множестве. Тем самым логическая интерпретациябулевой функции согласуется с ее алгебраической интерпретацией: булева функция есть операция (в алгебраическом смысле этого слова) на множестве истинностных значений. Тогда и понятие логической операции, которое было введено ранее, оказывается частным случаем общего понятия операции.

Будем обозначать через множество всехбулевых функций (для всех возможных значений числа переменных), а через— множество всехбулевых функций от переменных (для фиксированного). Из определения следует, что .

Итак, областью определения любой булевой функции от переменных является множество, т.е.булев куб размерности .Элементы булева куба называют n-мернымибулевыми векторами (или наборами). Число всех элементов булева куба составляет.Элементы булева куба будем также называть его вершинами.

Булев куб является носителембулевой алгебры (это же обозначение часто будем использовать и для соответствующего булева куба). Но в любой булевой алгебре определяется, как известно, естественное отношение порядкатак, что для произвольныхсоотношениевыполняется тогда и только тогда, когда(или, что равносильно,). Напомним, чтобулева алгебра является не чем иным, как n-й декартовой степенью двухэлементнойбулевой алгебры .

Употребляются также термины: единичный куб размерности , n-мерный единичныйкуб; вместо слова "куб" говорят также "гиперкуб".

Согласно общему принципу распространения отношения порядка на декартово произведение множествам. 4.5), для произвольных двух наборов иизимеет местотогда и только тогда, когдадля каждого, то есть.

Другими словами, тогда и только тогда, когдаили, адля каждого. Если существует хотя бы одно, для которого выполняется, то имеет место строгое неравенство. В частности, если существует ровно одно такое, то набордоминирует над набором, так как ясно, что в этом случае нельзя найти такой набор, что.