6.8. Параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока

К схеме на рис. 6.12 подключено синусоидальное напряжение . Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления. Определим ток на входе схемы.

Всоответствии с первым законом Кирхгофа:, (6.19) где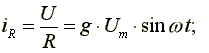- активная проводимость.

Рис. 6.12

Подставим эти формулы в уравнение (6.19). Получим:

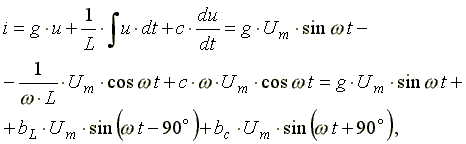, (6.20)

где 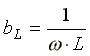- индуктивная проводимость;- емкостная проводимость.

Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o. Запишем уравнение (6.20) в комплексной форме.

, (6.21)

где - комплексная проводимость;- полная проводимость;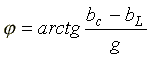- начальная фаза комплексной проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

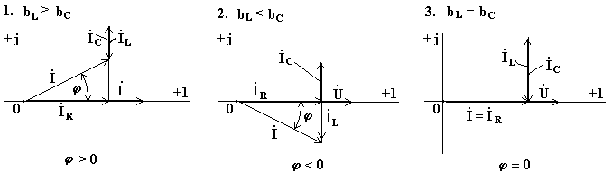Рис. 6.13 Рис. 6.14 Рис. 6.15

В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. Из условия возникновения резонанса 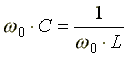тока получим формулу для резонансной частоты тока

.

В режиме резонанса тока полная проводимость цепи - минимальна, а полное сопротивление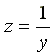- максимально. Ток в неразветвленной части схемы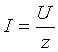в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

и .

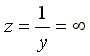Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.

6.9. Резонансный режим в цепи, состоящей из параллельно включенных реальной индуктивной катушки и конденсатора

Комплексная проводимость индуктивной ветви

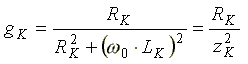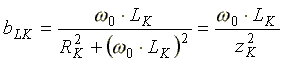где - активная проводимость индуктивной катушки;- полное сопротивление индуктивной катушки;- индуктивная проводимость катушки;- емкостная проводимость второй ветви.

В режиме резонансов токов справедливо уравнение:

или

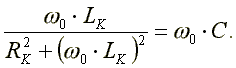
Из этого уравнения получим формулу для резонанса частоты

(6.22)

На рисунке 6.16 изображена векторная диаграмма цепи в резонансном режиме.

В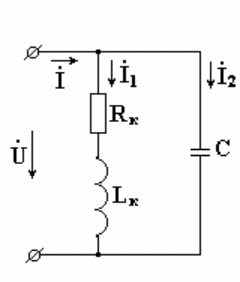ектор тока I₂ опережает вектор напряжения на 90^o. Вектор тока I₁ отстает от вектора напряжения на угол φ,

где .

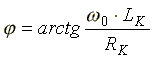Разложим вектор тока I₁ на две взаимно перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения, называется активной составляющей тока I_а1, другая - реактивной составляющей тока I_р1. Рис. 6.16

В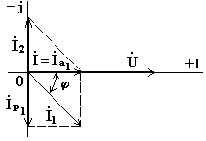режиме резонанса тока реактивная составляющая тока I_р1 и емкостный ток I₂ , направленные в противоположные стороны, полностью компенсируют друг друга, активная составляющая тока I_а1 совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной части схемы совпадает по фазе с напряжением. Рис. 6.17

6.10. Мощность в цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть мгновенные напряжение и ток определяются по формулам:

Тогда

(6.23)

Среднее значение мгновенной мощности за период

Из треугольника сопротивлений 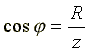, а.

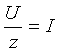Получим еще одну формулу:

.

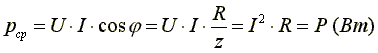Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P. Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию. Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90^o. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q. Преобразуем выражение (6.23):

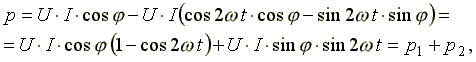
где - мгновенная мощность в активном сопротивлении;

- мгновенная мощность в реактивном элементе (в индуктивности или в емкости). Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью

,

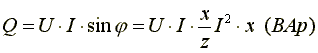
где x - реактивное сопротивление (индуктивное или емкостное). Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания. Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью. Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

,

где z - полное сопротивление цепи. Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности

,

где 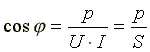- коэффициент мощности или "косинус "фи".

Коэффициент мощности является одной из важнейших характеристик электротехнических устройств. Принимают специальные меры к увеличению коэффициента мощности. Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 6.18).

И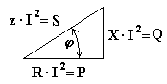з треугольника мощностей получим ряд формул:

, ,

Рис.6.18 ,. При анализе электрических цепей символическим методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока. Для цепи, имеющей индуктивный характер (R-L цепи)

,

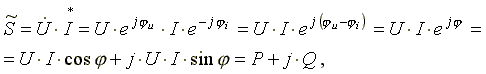где - комплекс напряжения;- комплекс тока;- сопряженный комплекс тока;- сдвиг по фазе между напряжением и током., ток как в R-L цепи, напряжение опережает по фазе ток.

Вещественной частью полной комплексной мощности является активная мощность. Мнимой частью комплексной мощности - реактивная мощность. Для цепи, имеющей емкостной характер (R-С цепи), . Ток опережает по фазе напряжение.

.

Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.