3.9.3. Квадратурная амплитудная модуляция (qam)

Очевидно, для кодирования передаваемой информации можно использовать не один параметр несущего колебания, а два одновременно.

Сигнал QAM можно также представить в виде синфазной и квадратурной составляющих

,

где - синфазная составляющая- го символа,

- квадратурная составляющая - го символа,

Рис. 3.42. Сигнальное созвездие модуляции

16-QAM

Квадратурная амплитудная модуляция (QAM – Quadrature Amplitude Modulation) также использует квадратурные несущие.

Однако, в отличие от QPSK, при которой каждый квадратурный канал модулируется с помощью двоичного сигнала, QAM использует передачу нескольких символов по обоим каналам и. Для примера на рис. 3.42 приведено сигнальное созвездие 16-QAM.

Рассмотрим принцип модуляции на примере 16-QAM. Практическое осуществление QAM-модуляции выполняется следующим образом. В памяти процессора хранится таблица значений модулирующего сигнала, соответствующего дибитам цифрового сообщения.

Таблица 3.2. Формирование сигнала 16-QAM

Сигнал	Значение
Дибит цифрового сообщения	00	01	11	10
Модулирующий сигнал , В	1	3	-3	-1

Процессор анализирует входную последовательность битов, разбивает ее на символы и для каждого символа выбирает соответствующие значения модулирующего сигнала из таблицы. Структурная схема QAM-модулятора представлена на рис. 3.43.

Рис. 3.43. Структурная схема 16-QAM модулятора

В соответствии с данной схемой система считывает две пары символов в каждый момент времени. Каждый дибит преобразуется в один из четырех возможных уровней напряжения (модулирующий сигнал в соответствии с табл. 3.2).Дибит имодулируют синфазную несущую, адибит имодулируют квадратурную несущую. Затем два модулированных колебания складываются, образуя единое квадратурно-модулированное колебание.

3.9.4. Частотные виды модуляции

В случае осуществления частотной модуляции параметром несущего колебания – носителем информации – является несущая частота . Модулированный радиосигнал имеет вид:

(3.23)

где – постоянная центральная частота сигнала, – девиация (изменение) частоты,– информационный символ,– начальная фаза.

Двоичная частотная модуляция (FSK)

В случае, если информационный символ имеет 2 возможных значения, имеет место двоичная частотная модуляция (FSK – Frequency Shift Keying). Сигнал, соответствующий информационному символу в (3.23) является полярным, т.е. принимает значения {-1,1}, где -1 соответствует значению исходного (неполярного) информационного символа 0, а 1 – единице. Таким образом, при двоичной частотной модуляции множеству значений исходного информационного символа {0,1} ставится в соответствие множество значений частоты модулированного радиосигнала. Вид сигнала FSK изображен на рис.3.44.

Из (3.23) следует непосредственная реализация FSK-модулятора: сигналы иимеют вид:

,

Так как функции ипринимают значения в интервале, то сигнальное созвездие сигнала FSK – окружность с радиусом.

Многопозиционная частотная модуляция (M-FSK)

Многопозиционная (многоуровневая) модуляция M-FSK формируется, как и другие многопозиционные виды модуляции, путем группировки бит в символы и введением взаимнооднозначного соответствия между множеством значений символа и множеством значений частоты модулированного колебания. Вид сигнала M-FSK также определяется (3.23), информационный сигнал M-FSK является полярным, как и для FSK. Как видно из (3.23), для того, чтобы значения частоты отличались на одинаковую величину, разность между значениями символов информационного сигнала должна быть одинаковой. Например, для сигнала 4-FSK множеству значений символов исходного информационного сигнала {00, 01, 10, 11} ставится во взаимнооднозначное соответствие множество значений модулирующего сигнала {-3, -1, 1, 3}.

Частотная модуляция с минимальным сдвигом (MSK)

Если частотная модуляция реализуется посредством выбора одного из независимых гармонических сигналов, то в общем случае при каждом переключении с -й на-ю позицию происходит разрыв фазы канального сигнала. Действительно, если-й гармонический сигнал

, (3.24)

то в момент коммутации имеем

.

При коммутации j-го генератора

.

Такие скачки фазы приводят к увеличению мощности боковых составляющих и к расширению спектра. Если (как обычно бывает на практике) после модулятора (в данном случае электронного коммутатора) включён полосовой фильтр, ограничивающий ширину спектра сигнала, то скачки фазы приводят к переходному процессу в фильтре. В результате этого возникает паразитная амплитудная модуляция сиг­нала, и пик-фактор сигнала (отношение его пиковой и средней мощностей) увеличивается. Кроме того, при использовании независимых генераторов для обеспечения ортогональности системы сигналов требуется разнос частот (i = 1, 2, ...), т.е. минимальный разнос .

С целью сужения спектра и сохранения минимального пик-фактора сигна­ла необходимо обеспечить непрерывность изменения мгновенной фазы сигна­ла при ещё меньших значениях . Частотную модуляцию с непрерывной фазой сокращённо обозначают ЧМНФ.

Запишем сигнал на отрезке при передачеi-й позиции символа:

, (3.25)

где .

При осуществлении ЧМНФ можно обеспечить ортогональность сигналов (3.25).Для ортогональных сигналов должно выполняться условие

. (3.26)

.

Откуда получаем

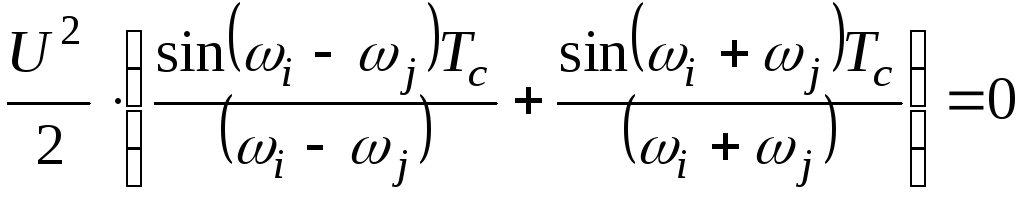. (3.27)

При вторым слагаемым можно пренебречь, оно много меньше первого. А первое слагаемое обращается в нуль при, где– целое число. Отсюда, минимальное значение между частотами манипуляции определяется выражениями:

, , (3.28)

Цифровую ЧМ с непрерывной фазой и параметром (3.28) называют моду­ляцией с минимальным (частотным) сдвигом - ММС (minimum shift keying -MSK).