3.7. Модели детерминированных цифровых сигналов в системе радемахера и уолша

Функции Радемахера образуются из синусо­идальных функций с помощью соотношения:

, ,

где аргумент — безразмерное время; Т — период функции, а положи­тельное целое число =0, 1, 2, ... — порядок функции;— знак действи­тельного числа; , при ипри. Иначе говоря, функции Радемахера, принимающие значения ±1, можно трактовать как функ­ции «прямоугольного синуса».

На рис. 3.21 приведены в качестве примера гра­фики первых четырех функций Радемахера для=0, 1, 2, 3. Легко видеть, что функцииортонормированы на интервале:

Дальнейшим развитием системы функции, имеющих форму «прямоугольной волны», является система функций Уолша {}. Она образуется сле­дующим образом. По определению вводится функция {}= 1 при=0.

Для получения функции придостаточно записать числот в двоичной системе счисления, т. е. представить суммой

где — положительные целые числа.

При: этом функция Уолша .

Порядок функции Уолша - равен числу знакоперемен на интервале (0, 1/2) и определяется какдля четныхт и для нечетныхт.

На рис. 3.22 приведены графики первых восьми функций Уолша ,,…,, построенных по четырем функциям Радемахера.

3.8. Импульсно – модулированные сигналы

При импульсной модуляции в качестве носителя модулированных сигналов используются последовательности импульсов, как правило – прямоугольных. В беспроводных системах передачи данных (в радиосвязи) эти последовательности заполняются высокочастотными колебаниями, создавая тем самым двойную модуляцию.

При использовании в качестве несущих сигналов периодических последовательностей импульсов (например, прямоугольных) свободными параметрами модуляции (рис.3.23) могут быть

- амплитуда импульсов,

- длительность импульсов,

- частота следования импульсов,

- фаза (положение импульса относительно тактовой точки) импульсов.

Рис. 3.23. Периодическая последовательность прямоугольных импульсов. - период следования, - длительность импульса, - амплитуда импульса, - начальная фаза, определяющая временное положение центров импульсов.

Аналитическая запись последовательности импульсов:

,

где - одиночный импульс.

Параметры сигнала:

–амплитуда импульса;

- длительность импульса;

- период следования импульсов (период повторения);

- частота следования импульсов;

- начальная фаза, определяющая временное положение центров импульсов.

Это дает четыре основных вида импульсной модуляции: АИМ, ШИМ, ЧИМ и ФИМ.

Как правило, эти виды модуляции применяются при передаче дискретизированных данных. Для прямоугольных импульсов наиболее широко используются амплитудно-импульсная (АИМ) и широтно-импульсная (ШИМ) модуляция.

3.8.1. Амплитудно-импульсная модуляция (АИМ)

Амплитудно-импульсная модуляция заключается в изменении приращения амплитуды импульсов пропорционально функции управляющего сигнала при постоянной длительности импульсов и периоде их следования:

, (3.11)

, , .

Рис. 3.24.АИМ однотональным сигналом s(t)

Рассмотрим пример модулирования однотонального сигнала , приведенного на рис. 3.24. Запишем уравнение модулированного сигнала в следующей форме:

, (3.12)

где – периодическая последовательность прямоугольных импульсов с частотой , которую можно аппроксимировать рядом Фурье (без учета фазы):

. (3.13)

Подставляя (3.13) в (3.12), получим:

(3.14)

Форма спектра, в начальной части спектрального диапазона, приведена на рис. 3.25.

Рис. 3.25. Сигнал АИМ и его спектр

В целом, спектр бесконечен, что определяется бесконечностью спектра прямоугольных импульсов. Около каждой гармоники спектра прямоугольных импульсов появляются боковые составляющие, соответствующие спектру моделирующей функции (при многотональном сигнале – боковые полосы спектров). При дополнительном высокочастотном заполнении импульсов весь спектр смещается в область высоких частот на частоту заполнения.

3.8.2 Широтно-импульсная модуляция (ШИМ)

Широтно-импульсная модуляция (модуляция по длительности импульсов (ДИМ)), заключается в управлении длительностью импульсов пропорционально функции управляющего сигнала при постоянной амплитуде импульсов и периоде следования по фронту импульсов:

, (3.15)

, , .

Рис. 3.26. Широтно-импульсная модуляция.

Рис. 3.27. Спектр ШИМ – сигнала

Рис. 3.28. Восстановленный сигнал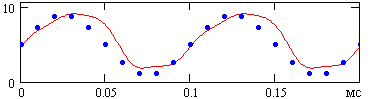

На рис. 3.27 приведен спектр сформированного сигнала ШИМ. В начальной части спектра он содержит постоянную составляющую среднего уровня сигнала и пик частоты гармоники, закодированной в ШИМ – сигнале. Если выделить из спектра эти две составляющие, то восстанавливается исходный сигнал с погрешностью квантования, приведенный на рис. 3.28. Естественно, что при малом числе уровней квантования погрешность восстановления исходного гармонического сигнала очень велика.

Попутно заметим, что широтно-импульсная модуляция с последующим выделением постоянной составляющей может весьма эффективно использоваться (и используется) для слежения за средним уровнем сигнала и автоматического регулирования его динамического диапазона, как, например, в системах установки громкости звука и яркости цветов и изображения в целом в современных телевизионных установках.

3.8.3. Временная импульсная модуляция (ВИМ)

Временная импульсная модуляция (ВИМ) представляет собой девиацию импульсов по временной оси по закону модулирующего сигнала, и по существу аналогична угловой модуляции гармонической несущей. Она также может быть фазовой (ФИМ) или частотной (ЧИМ).

Частотно-импульсная модуляция.

, (3.16)

, ,.

Фазо-импульсная модуляция.

, (3.17)

, ,.

Временные диаграммы этих видов модуляции показаны на рис.3.29.

Рис.3.29. Временные диаграммы ФИМ и ЧИМ сигналов