Методические указания КДМ

2. Кодовий замок має m однакових комірок, кожну з яких можна встановити у n стійких положень (p цифр, q літер). Скільки різноманітних комбінацій необхідно перебрати, щоб не знаючи коду відчинити замок, якщо відомі додаткові умови (табл. 8.18).

Таблиця 8.18 – Параметри для завдання

Продовження табл.8.18

Тема 11. Біном Ньютона. Формули включення та виключення, рекурентні співвідношення, продуктивні функції

1. Задано поліном: (a·xb+c·yd)e за допомогою бінома Ньютона. Визначити у розкладанні бінома Ньютона коефіцієнт С, який відповідає елементу С· xf ·yg (табл. 8.19).

Таблиця 8.19 – Параметри для завдання

2. У a – процесорний ЕОМ b мікропроцесорів обробляють текстову інформацію, c – графічну, d – символьну, e мікропроцесорів одночасно обробляють графічну та текстову, f – текстову та символьну, g – графічну та символьну, а частина мікропроцесорів одночасно обробляють графічну, текстову та символьну інформацію (табл. 8.20). Визначити кількість способів

61

виконання заданої у таблиці 8.21 категорії, чи можлива реалізація такої категорії?

Таблиця 8.20 – Значення параметрів a, b, c, d, e, f, g

Продовження табл.8.21

Кількість способів…

11.Обрати 2 мікропроцесора, кожний з яких обробляє більш одного виду інформації

12.Обрати 2 універсальних мікропроцесора

13.Розмістити мікропроцесори, які обробляють символьну інформацію, на мікросхемі за умовою, що спочатку повинні йти універсальні мікропроцесори, потім ті, які обробляють 2 видами інформації, потім ті, які обробляють тільки символьну інформацію.

14.Обрати 15 мікропроцесорів, які обробляють тільки графічну інформацію (без урахування порядку)

15. Обрати 7 мікропроцесорів, які обробляють тільки текстову інформацію (без урахування порядку)

16.Обрати 9 мікропроцесорів, які обробляють тільки символьну інформацію (без урахування порядку)

17.Обрати 25 мікропроцесорів, які обробляють тільки графічну інформацію (з урахуванням порядку)

18.Обрати 15 мікропроцесора, які обробляють тільки текстову інформацію (з урахуванням порядку)

19.Обрати 17 мікропроцесора, які обробляють тільки символьну інформацію (з урахуванням порядку)

20.Розмістити мікропроцесори, які обробляють на мікросхемі тільки графічну інформацію

21.Розмістити мікропроцесори, які обробляють на мікросхемі тільки текстову інформацію

22.Розмістити мікропроцесори, які обробляють на мікросхемі тільки символьну інформацію

23.Обрати 2 мікропроцесора, кожний з яких обробляє тільки 1 вид інформації

24.Обрати 2 мікропроцесора, кожний з яких обробляє більш одного виду інформації

25.Обрати 2 універсальних мікропроцесора

26.Обрати 3 мікропроцесора, які обробляють тільки графічну інформацію (без урахування порядку)

27.Обрати 3 мікропроцесора, які обробляють тільки символьну інформацію (без урахування порядку)

28. Обрати 2 мікропроцесора, які обробляють тільки текстову інформацію (без урахування порядку)

29.Обрати 25 мікропроцесорів, які обробляють тільки графічну символьну інформацію (з урахуванням порядку)

30.Обрати 15 мікропроцесорів, які обробляють тільки текстову інформацію (з урахуванням порядку)

64

3. Скільки дільників мають числа, які наведено у таблиці 8.22.

Таблиця 8.22

4. Знайти ряд, для якого продуктивною є функція, яку наведено у таблиці

8.23.

Таблиця 8.23 – Продуктивна функція

a f (n 2) b f (n 1) c f (n) 0, f(1)=d, f(2)=e. Значення параметрів a, b, c, d, e

наведено у таблиці 8.24.

65

Таблиця 8.24 – Значення параметрів a, b, c, d, e

9 ПРИКЛАД РОЗВ’ЯЗАННЯ ДЕЯКИХ ТИПОВИХ ЗАВДАНЬ

Завдання 1. Задано універсальну множину U та чотири її підмножини А,

В, C, D.

U = {1, 2, 3, ... , 30}; A={a U | a=5 ∙ i}; B={b U | b=8 ∙ i}; C={c U | c=6 ∙ i}; i=1,2,3,...n.

Якщо i=1,...,6, то А = {5 ∙ i} = {5, 10, 15, 20, 25, 30}. Якщо i=1,..., 3, то B = {8 ∙ i} = {8, 16, 24}.

Якщо i=1,...,5, то C = {6 ∙ i} = {6, 12, 18, 24, 30}.

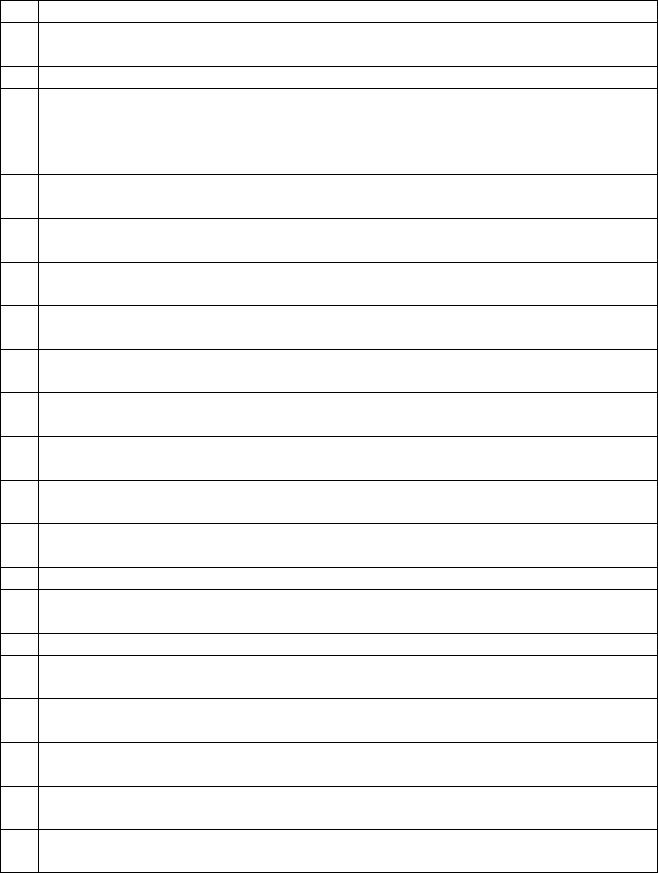
Для відображення множин за допомогою кругів Ейлера (рис. 9.1) знайдемо вирази A B, A C та B C.

A B = { };

A C = {30};

B C = {24}.

Таким чином, розподіл елементів на кругах Ейлера можна зобразити наступним чином (рис. 9.1).

Спростимо функцію.

F A B\C B (A B) (C B) A B (C B)

A B C A B B A B C A A B C A B C

66

В

8, 16

С24

6, 12, 18

А

30

5, 10, 15, 20, 25

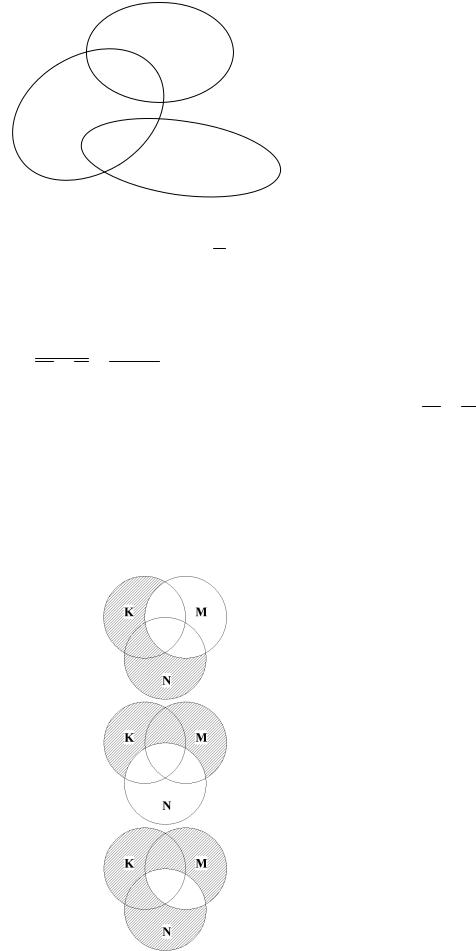
Рисунок 9.1 – Відображення множин за допомогою кругів Ейлера

Знайдемо потужність множини A B C.

F= ; |F| = 0.

Завдання 2.

Для формули F M N K N побудувати діаграму Венна. Проілюструємо на діаграмі Венна задану формулу, виконавши спочатку

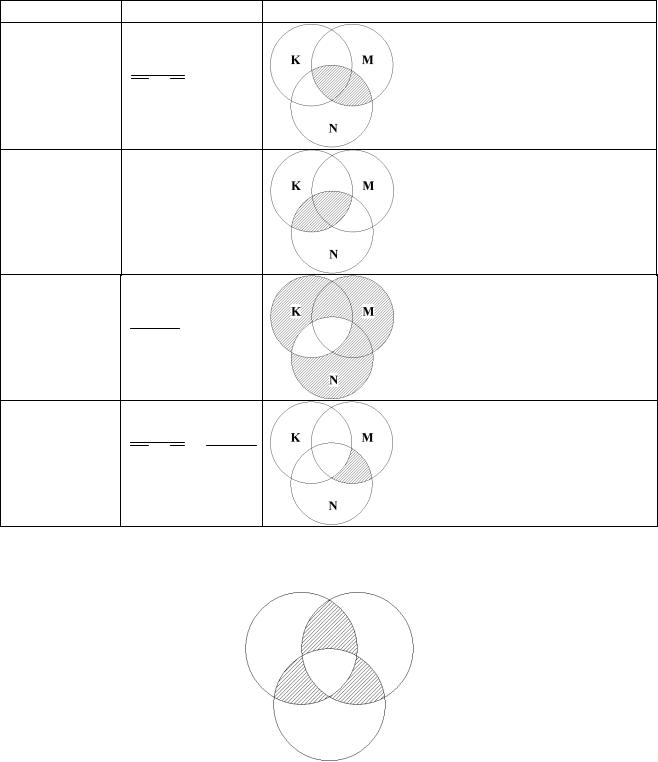
Продовження табл.9.1

4M N

5K N

6K N

7M N K N

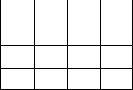
Завдання 3. Записати формулу для діаграми Венна, яку зображено на рисунку 9.2.

A B

C

Рисунок 9.2 – Діаграма Венна

Запишемо формулу пошарово. Розрахунки подамо за допомогою таблиці

9.2

68

Таблиця 9.2 – Запис формули за допомогою діаграм Венна

Таким чином, одержуємо формулу, відповідну до заданої діаграми Венна:

((A B A C B C) \ A B C) .

Завдання 4. В результаті опитування виявлено реакцію деякої кількості глядачів на одну телевізійну передачу. Усіх глядачів і їх реакцію можна виразити в термінах таких чотирьох категорій: Ч (чоловічої статі), Д (дорослий), С (сподобалося), Ду (дуже). Результати розподілення глядачів наведено у таблиці 9.3. Обчислити кількість глядачів, що попадають у категорію Ч С Ду .

Таблиця 9.3 – Розподілення глядачів за категоріями

Обчислимо кількість людей, які потрапляють до заданої категорії: 3+5=8.

Завдання 5. Задано множини А={4,2,0}; В={3,1}. Знайти декартовий добуток А В, А2, А3.

А В={(4,3),(4,1),(2,3),(2,1),(0,3),(0,1)}. А2={(4,4),(4,2),(4,0),(2,4),(2,2),(2,0),(0,4),(0,2),(0,0)}. А3={(4,4,4),(4,4,2),(4,4,0),(4,2,4),(4,2,2),(4,2,0),(4,0,4),(4,0,2),(4,0,0),

(2,4,4),(2,4,2),(2,4,0),(2,2,4),(2,2,2),(2,2,0),(2,0,4),(2,0,2),(2,0,0),

(0,4,4),(0,4,2),(0,4,0),(0,2,4),(0,2,2),(0,2,0),(0,0,4),(0,0,2),(0,0,0)}.

Завдання 6. Задано бінарне відношення R={(1,1),(2,2), (3,1),((4,4)} як перелік елементів на множині А={1,2,3,4}, R1 A2.

1.Задати відношення R за допомогою матриці та графа.

2.Записати властивості відношення R. Перевірити чи є відношення R відношенням еквівалентності, толерантності, порядку?

3.Визначити, чи є дане відношення функціональним, відображенням? Якщо є, визначити тип відображення. Відповідь обґрунтувати.

1.Задамо бінарне відношення за допомогою матриці.

31

41

Задамо бінарне відношення за допомогою графа.

70