ЗМІСТ
Вступ 4
1 Непараметричні методи оцінювання законів розподілу випадкової
величини 5
2 Параметричне оцінювання закону розподілу випадкової величини 18
3 Перевірка статистичних гіпотез про закон розподілу випадкової
величини 30
Рекомендована література 40
Додаток А. Варіанти завдань 41
Додаток Б. Основні закони розподілу неперервних випадкових величин 50
Додаток В. Основні таблиці 55
Загальні вказівки
Статистичний аналіз даних є необхідним етапом аналізу і дослідження будь-якої виробничо-господарської, фінансової або комерційної діяльності як окремої фірми, підприємства або організації, так і сукупності підприємств і організацій, галузі або країни в цілому. Статистичний аналіз це одночасно і наука, і мистецтво отримання корисної інформації з даних, отриманих у результаті спостережень реалізацій випадкових величин.
Методи статистичного аналізу даних є формальними процедурами, що дозволяють за вибіркою реалізацій випадкової величини оцінити закон розподілу, обчислити вибіркові характеристики розподілу випадкової величини, провести перевірку статистичних гіпотез про закон розподілу випадкової величини і його параметрів. Крім того, якщо задані вибірки реалізацій двох і більше випадкових величин, можна провести дослідження про наявність стохастичного зв'язку між цими величинами.
Метою даних методичних вказівок є вивчення методів статистичного аналізу даних і розвитку практичних навичок їх використання.
Методичні вказівки містять необхідний для кожного студента теоретичний і довідковий матеріал, приклади виконання завдання, індивідуальні завдання, вказівки до порядку виконання кожного завдання, форму звіту і контрольні запитання.
Перед виконанням завдання студент повинен вивчити основні теоретичні положення, розглянути постановку задачі, виписати розрахункові формули, опрацювати контрольні запитання та завдання. Після виконання завдання необхідно оформити звіт.
1 Непараметричні методи оцінювання законів розподілу випадкової величини
Мета завдання
Вивчити непараметричні методи оцінювання законів розподілу випадкової величини за вибіркою, навчитися застосовувати ці методи під час аналізу статистичних даних.
1.2 Методичні вказівки з організації самостійної роботи студентів
Попередньою вимогою для виконання завдання є засвоєння таких теоретичних знань: випадкові величини, закони розподілу неперервних випадкових величин (показовий, рівномірний, нормальний), функція та щільність розподілу, інтервальний варіаційний ряд, гістограма та емпірична функція розподілу.
1.3 Основні положення
Непараметричний
метод оцінювання закону розподілу
випадкової величини
полягає в оцінюванні форми розподілів
за вибіркою реалізації випадкової
величини
без припущення, що закон розподілу
є
відомою функцією з точністю до
параметрів. Внаслідок такого оцінювання
одержують статистичний аналог закону
розподілу випадкової величини.
Якщо
обсяг вибірки достатньо великий (
>500),
то для побудови статистичного аналога
закону розподілу випадкової величини
використовується інтервальний варіаційний
ряд, у якому значення реалізацій
випадкової величини
групуються по інтервалах.
При виборі рівних інтервалів ширина інтервалів визначається за формулою:
,
(1.1)
де
– розмах варіаційного ряду;
–
максимальне
значення реалізації випадкової величини
у вибірці;
–
мінімальне
значення реалізації випадкової величини
у вибірці;
n – обсяг вибірки;
k – число інтервалів (ціла частина знаменника, округленого у більшу сторону).
При
обсязі вибірки 100£
n£
500
кількість інтервалів має бути в межах
k=10¸30.
Тоді ширина інтервалу
може бути визначена за формулою:
.
(1.2)
Для побудови шкали інтервалів за нижню межу першого інтервалу приймається величина
.
(1.3)
Нижня межа другого інтервалу збігається з верхньою межею першого і дорівнює:
.
(1.4)
Цей процес продовжується до k-го інтервалу, причому за верхню межу
останнього інтервалу приймаємо величину
.
(1.5)
Визначивши шкалу інтервалів, виконують розподіл елементів вибірки (варіантів) за інтервалами, перебираючи їх у порядку запису за вибіркою.
Якщо
значення варіанта збігається з межею
інтервалу, то це значення відносять до
інтервалу, що лежить зліва від границі,
з якою він збігається (крім значення
варіанта
,
яке слід віднести до першого інтервалу).
Розподіливши варіанти за інтервалами, для кожного інтервалу визначають такі величини:
1)
частоту потрапляння
до інтервалу;
2)
частість або відносну частоту
потрапляння в інтервал, згідно з формулою:
;
(1.6)
3) представник інтервалу:
.
(1.7)
У результаті одержуємо інтервальний варіаційний ряд, поданий у табл.1.1
Таблиця 1.1 – Інтервальний варіаційний ряд
Номер інтервалу |
1 |
2 |
... |
i |
... |
K |
Межа інтервалу
|
|
|
... |
|
... |
|
Частість потрапляння
в інтервал
|
|
|
... |
|
.. |
|
Частість
потрапляння
в інтервал
|
|
|
... |
|
... |
|
Представник
інтервалу
|
|
|
... |
|
... |
|
Щільність відносної
частоти
|
|
|
... |
|
... |
|
Для
побудови статистичного аналогу щільності
розподілу
випадкової величини
табл. 1.1 доповнюється рядком, у якому
розташовується щільність відносної
частоти
,
яка визначається у такий спосіб:
.
(1.8)
Для
графічного зображення варіаційного
ряду існує гістограма, що являє собою
ряд зімкнутих прямокутників, основою
кожного з яких є ширина інтервалу
,
а висота дорівнює або частоті
,
або частості
,
або щільності відносної частоти
.
В останньому випадку гістограма є
аналогом щільності розподілу
випадкової величини
.
Таку гістограму називають гістограмою
відносних частот. На рис. 1.1 подано всі
три типи гістограм.
x
ni
pi*
hi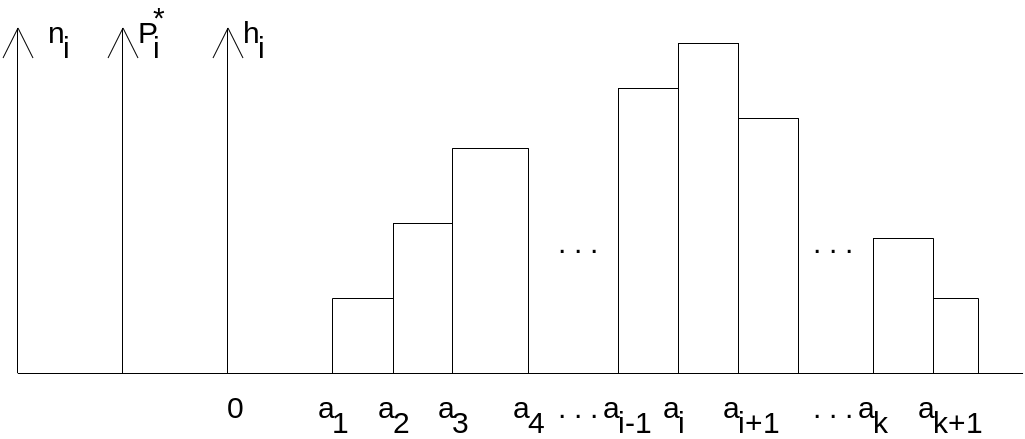
Рисунок 1.1 – Гістограми
Статистичним
аналогом функції розподілу
випадкової величини X
є емпірична функція розподілу
,
визначена у такий спосіб:
.
(1.9)
Емпірична функція розподілу будується за інтервальним варіаційним рядом відповідно до виразів:
……………………………………. (1.10)
Точки
з координатами
наносять на графік і з'єднують відрізками
прямої. Графічне зображення емпіричної
функції розподілу подане на рис. 1.2.
0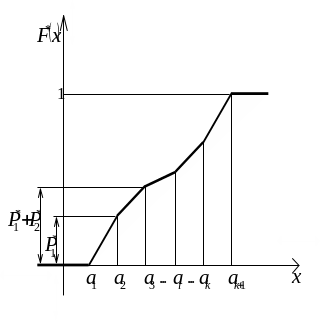
Рисунок 1.2 – Емпірична функція розподілу
Аналіз
виду статистичних аналогів щільності
розподілу
і функції розподілу
випадкової величини X
дозволяють висунути гіпотезу про її
закон розподілу.
Основні закони розподілу неперервних випадкових величин, графіки щільності розподілу і функції розподілу, їхні аналітичні вирази і формули для обчислення основних числових характеристик наведені в додатку Б.
1.4 Приклади виконання завдання
Приклад 1.1 Нехай випадкова величина задана вибіркою обсягу =40 (табл. 1.2).
Таблиця 1.2 – Вибірка реалізації випадкової величини
-
3,18
6,42
4,87
7,49
7,16
5,58
10,44
9,16
3,85
2,42
4,83
3,47
3,62
3,94
3,03
2,29
6,79
8,59
2,07
4,58
5,27
6,09
7,95
10,76
4,49
7,16
8,89
7,49
-0,97
12,91
7,44
7,04
2,71
9,57
-0,86
8,89
9,27
5,45
6,57
7,67
Побудувати
інтервальний варіаційний ряд (вибрати
кількість інтервалів
=8),
гістограму відносних частот, емпіричну
функцію розподілу, висунути гіпотезу
щодо закону розподілу випадкової
величини
.
Розв'язок
Знайдемо
мінімальне
та максимальне значення реалізації
випадкової величини у вибірці:
Отже,
розмах варіювання дорівнює
.
Тоді ширина інтервалу
.
Знайдемо границі інтервалів та визначимо
частоту
,
відносну частоту
,
щільність відносної частоти
потрапляння елементів вибірки в
-й
інтервал і представників
-го
інтервалу.
Тоді інтервальний варіаційний ряд матиме вигляд таблиці (табл. 1.3).
Таблиця 1.3 – Інтервальний варіаційний ряд
Номер -го інтервалу |
-й
інтервал
|
Частота
потрапляння
в
-й
інтервал:
|
Відносна
частота потрапляння
в
-й
інтервал:
|
Представник
-го
інтервалу:
|
Щільність
відносної частоти:
|
1 |
|
2 |
0,05 |
-0,1025 |
0,0288184 |
2 |
|
3 |
0,075 |
1,6325 |
0,0432277 |
3 |
|
7 |
0,175 |
3,3675 |
0,100865 |
4 |
|
7 |
0,175 |
5,1025 |
0,100865 |
5 |
|
11 |
0,275 |
6,8375 |
0,158501 |
6 |
|
6 |
0,15 |
8,5725 |
0,0864553 |
7 |
|
3 |
0,075 |
10,3075 |
0,0432277 |
8 |
|
1 |
0,025 |
12,0425 |
0,0144092 |
Емпірична функція розподілу будується за інтервальним варіаційним рядом за формулою (1.10), її значення наведені в табл. 1.4.
Таблиця 1.4 – Емпірична функція розподілу
|
-0,97 |
0,765 |
2,5 |
4,235 |
5,97 |
7,705 |
9,44 |
11,175 |
12,91 |
|
0 |
0,05 |
0,125 |
0,3 |
0,475 |
0,75 |
0,9 |
0,975 |
1 |
Гістограма
відносних частот для побудованого
варіаційного ряду зображена на рис.
1.3, емпірична функція розподілу
– на рис. 1.4.
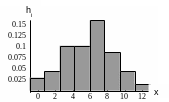
Р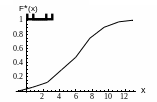
исунок
1.3 – Гістограма відносних частот
Рисунок 1.4 – Емпірична функція розподілу
Для того, щоб висунути гіпотезу відносно закону розподілу випадкової величини , гістограма відносних частот порівнюється з графіком щільності розподілу , графік емпіричної функції розподілу порівнюється з графіком функції розподілу (Додаток Б).
Аналіз гістограми та емпіричної функції розподілу дозволяють висунути гіпотезу про те, що задана випадкова величина має нормальний закон розподілу.
Щільність нормального закону розподілу випадкової величини X має вигляд:
.
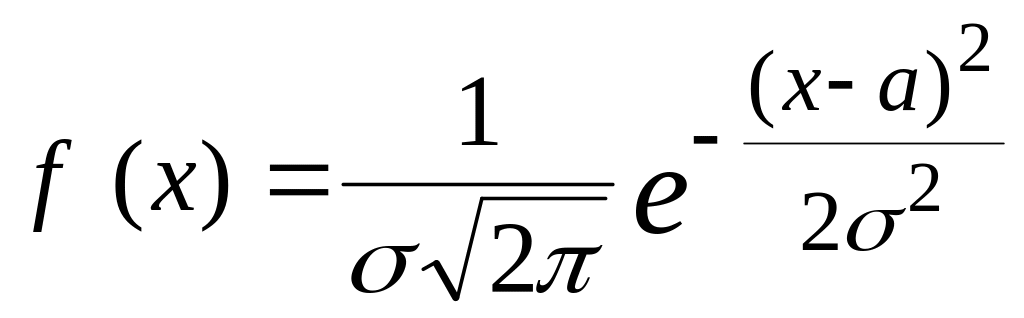(1.11)
Ф
ункція
розподілу визначається формулою:
.
(1.12)
Приклад 1.2
Нехай випадкова величина задана вибіркою обсягу =100 (табл. 1.5).
Таблиця 1.5 – Вибірка реалізації випадкової величини
-
0,59
0,36
0,99
0,23
0,10
3,46
1,56
0,43
0,33
1,27
3,54
0,95
1,76
0,24
0,20
0,07
1,32
3,54
0,27
0,78
1,78
0,56
0,10
1,85
0,48
0,14
0,63
1,00
0,33
0,17
1,14
0,33
5,52
0,58
1,23
1,10
0,18
0,26
0,74
0,90
0,56
0,29
0,33
0,05
0,92
1,74
0,19
0,23
0,24
1,18
1,22
0,85
2,69
0,75
0,02
0,34
2,75
0,09
0,37
0,97
1,46
1,97
1,55
0,02
0,40
0,92
0,70
3,58
1,32
1,50
0,39
1,43
0,72
0,08
0,96
0,20
0,87
0,80
0,89
2,26
1,04
0,62
0,32
0,32
2,10
0,92
0,67
0,28
0,78
7,03
4,04
0,32
1,64
0,25
1,06
0,72
0,34
0,14
0,03
0,39
Побудувати інтервальний варіаційний ряд (вибрати кількість інтервалів =10), гістограму відносних частот, емпіричну функцію розподілу, висунути гіпотезу щодо закону розподілу випадкової величини .
Розв'язок
Знайдемо мінімальне та максимальне значення реалізації випадкової величини у вибірці, розмах варіювання, ширину інтервалу:
;
;
.
Побудуємо інтервальний варіаційний ряд, як у прикладі 1.1, отримаємо табл. 1.6.
Таблиця 1.6 – Інтервальний варіаційний ряд
Номер -го інтервалу |
-й інтервал |
Частота потрапляння в -й інтервал: |
Відносна частота потрапляння в -й інтервал: |
Представник -го інтервалу: |
Щільність відносної частоти: |
1 |
|
51 |
0,51 |
0,3705 |
0,727 |
2 |
|
27 |
0,27 |
1,0715 |
0,385 |
3 |
|
12 |
0,12 |
1,7725 |
0,171 |
4 |
|
3 |
0,03 |
2,4735 |
0,043 |
5 |
|
1 |
0,01 |
3,1745 |
0,014 |
6 |
|
4 |
0,04 |
3,8755 |
0,057 |
7 |
|
0 |
0 |
4,5765 |
0 |
8 |
[4,927; 5,628] |
1 |
0.01 |
5,2775 |
0,014 |
9 |
[5,628; 6,329] |
0 |
0 |
5,9785 |
0 |
10 |
[6,329; 7,03] |
1 |
0,01 |
6,6795 |
0,014 |
Емпірична функція розподілу будується за інтервальним варіаційним рядом за формулою (1.10), її значення наведені в табл. 1.7.
Таблиця 1.7 – Емпірична функція розподілу
|
0,02 |
0,721 |
1,422 |
2,123 |
2,824 |
3,525 |
4,226 |
4,927 |
5,628 |
6,329 |
7,03 |
|
0 |
0,51 |
0,78 |
0,90 |
0,93 |
0,94 |
0,98 |
0,98 |
0,99 |
0,99 |
1.0 |
Гістограма відносних частот для побудованого варіаційного ряду зображена на рис. 1.5, емпірична функція розподілу – на рис. 1.6.
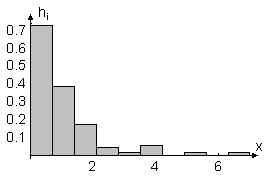
Рисунок 1.5 – Гістограма відносних частот
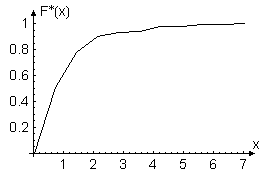
Рисунок 1.6 – Емпірична функція розподілу
Аналіз гістограми та емпіричної функції розподілу дозволяють висунути гіпотезу про те, що задана випадкова величина має показниковий закон розподілу.
Щільність розподілу показникового закону розподілу випадкової величини X має вигляд:
.
(1.13)
Функція розподілу визначається формулою:
.
(1.14)
Приклад 1.3
Нехай випадкова величина задана вибіркою обсягу =100 (табл. 1.8).
Таблиця 1.8 – Вибірка реалізації випадкової величини
-
6,44
5,88
2,26
3,65
8,16
7,11
7,30
4,82
3,83
3,54
5,11
3,08
7,79
5,60
3,13
1,82
7,34
1,66
1,16
3,78
8,12
8,89
2,78
6,97
1,68
3,01
0,52
3,32
2,52
4,89
2,22
7,50
7,68
1,35
6,10
4,41
8,88
4,74
2,97
2,59
1,54
3,08
1,81
7,80
2,41
3,18
8,02
0,82
0,72
0,18
7,49
6,50
7,20
4,28
5,27
8,01
8,52
2,93
8,16
3,58
8,63
7,18
5,18
0,99
7,09
4,10
3,37
2,18
4,68
0,91
4,35
1,35
3,95
0,73
5,85
3,85
5,75
5,44
0,58
4,85
6,23
2,51
1,42
1,26
6,58
4,32
5,23
0,27
8,49
0,22
1,85
7,08
3,80
8,30
6,50
5,72
8,84
7,57
0,64
1,86
Побудувати інтервальний варіаційний ряд (вибрати кількість інтервалів =10), гістограму відносних частот, емпіричну функцію розподілу, висунути гіпотезу щодо закону розподілу випадкової величини .
Розв'язок
Знайдемо мінімальне та максимальне значення реалізації випадкової величини у вибірці, розмах варіювання, ширину інтервалу:
;
;
.
Побудуємо інтервальний варіаційний ряд, як у прикладі 1.1, отримаємо табл. 1.9.
Таблиця 1.9 – Інтервальний варіаційний ряд
Номер -го інтервалу |
-й інтервал |
Частота потрапляння в -й інтервал: |
Відносна частота потрапляння в -й інтервал: |
Представник -го інтервалу: |
Щільність відносної частоти: |
1 |
|
11 |
0,11 |
0,6155 |
0,126 |
2 |
|
12 |
0,12 |
1,4865 |
0,138 |
3 |
|
8 |
0,08 |
2,3575 |
0,092 |
4 |
|
12 |
0,12 |
3,2285 |
0,138 |
5 |
|
10 |
0,10 |
4,0995 |
0,115 |
6 |
|
9 |
0,09 |
4,9705 |
0,103 |
7 |
|
8 |
0,08 |
5,8415 |
0,092 |
8 |
[6,277; 7,148] |
8 |
0,08 |
6,7125 |
0,092 |
9 |
[7,148; 8,019] |
11 |
0,11 |
7,5835 |
0,126 |
10 |
[8,019; 8,89] |
11 |
0,11 |
8,4545 |
0,126 |
Емпірична функція розподілу будується за інтервальним варіаційним рядом за формулою (1.10), її значення наведені в табл. 1.10.
Таблиця 1.10 – Емпірична функція розподілу
|
0,18 |
1,051 |
1,922 |
2,793 |
3,664 |
4,535 |
5,406 |
6,277 |
7,148 |
8,019 |
8,89 |
|
0 |
0,11 |
0,23 |
0,31 |
0,43 |
0,53 |
0,62 |
0,7 |
0,78 |
0,89 |
1,0 |
Гістограма відносних частот для побудованого варіаційного ряду зображена на рис. 1.7, емпірична функція розподілу – на рис. 1.8.
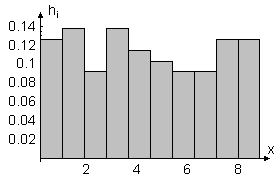
Рисунок 1.7 – Гістограма відносних частот
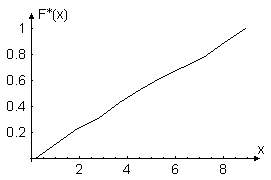
Рисунок 1.8 – Емпірична функція розподілу
Аналіз гістограми відносних частот та емпіричної функції розподілу дозволяють висунути гіпотезу про те, що задана випадкова величина має рівномірний закон розподілу.
Щільність розподілу рівномірного закону розподілу випадкової величини X має вигляд:
.
(1.15)
Ф ункція розподілу визначається формулою:
.
(1.16)
1.5 Індивідуальні завдання
За своїм номером у журналі академгрупи вибрати з табл. А.1 дані реалізацій випадкової величини X і сформувати вибірку обсягом n=100.
Вивчити метод непараметричного оцінювання закону розподілу випадкової величини.
Виписати розрахункові формули і побудувати інтервальний варіаційний ряд (заповнити табл. 1.1).
За інтервальним варіаційним рядом побудувати гістограму для щільності відносної частоти (рис. 1.1) та емпіричну функцію розподілу (рис. 1.2).
Висунути гіпотезу про закон розподілу випадкової величини X.
Навести формули щільності розподілу та функції розподілу закону розподілу, відносно якого висунута гіпотеза.
Дані для виконання завдання вміщені в табл. А.1.
1.6 Зміст звіту
Звіт має містити: мету завдання, основні розрахункові формули, вибірку, інтервальний варіаційний ряд, гістограму, емпіричну функцію розподілу, гіпотезу про закон розподілу заданої випадкової величини, формули щільності розподілу та функції розподілу закону розподілу, відносно якого висунута гіпотеза.
1.7 Контрольні запитання
1. У чому полягає непараметричний спосіб оцінювання закону розподілу випадкової величини?
2. Що являє собою інтервальний варіаційний ряд і для чого він призначений?
3. Які існують типи гістограм і як вони будуються?
4. Що таке емпірична функція розподілу і як вона будується?