shpora_fizika

30). Давление света

Давлением света называется давление, которое производят электромагнитные световые волны, падающие на поверхность какого-либо тела. Существование такого давления было предсказано Дж. Максвеллом в его электромагнитной теории света. Если, например, электромагнитная волна падает на металл, то под действием электрического поля волны с напряженностью  электроны поверхностного слоя металла будут двигаться в направлении, противоположном вектору  со скоростью  Магнитное поле волны действует на движущиеся электроны с силой Лоренца F_Л в направлении, перпендикулярном поверхности металла (согласно правилу левой руки). Давление р, оказываемое волной на поверхность металла, можно рассчитать как отношение равнодействующей сил Лоренца, действующих на свободные электроны в поверхностном слое металла, к площади поверхности металла:

На основании электромагнитной теории Максвелл получил формулу для светового давления. ,где J — интенсивность света,  — коэффициент отражения света , с — скорость света в вакууме. Для зеркальных поверхностей  при полном поглощении (для абсолютно черного тела) .С точки зрения квантовой теории, давление является следствием того, что у фотона имеется импульс . Пусть свет падает перпендикулярно поверхности тела и за 1 с на 1 м² поверхности падает N фотонов. Часть из них поглотится поверхностью тела (неупругое соударение), и каждый из поглощенных фотонов передает этой поверхности свой импульс .Часть же фотонов отразится (упругое соударение). Отраженный фотон полетит от поверхности в противоположном направлении. Полный импульс, переданный поверхности отраженным фотоном, будет равен.Давление света на поверхность будет равно импульсу, который передают за 1 с все N фотонов, падающих на 1 м² поверхности тела. Если  — коэффициент отражения света от произвольной поверхности, то  — это число отраженных фотонов, а  — число поглощенных фотонов. Следовательно, давление светаПроизведение представляет собой энергию всех фотонов, падающих на 1 м² поверхности за 1 с. Это есть интенсивность света (поверхностная плотность потока излучения падающего света): .Таким образом, давление света 

31). Эффект Комптона

Комптон исследовал упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. Открытый им эффект увеличения длины волны рассеянного излучения, названный впоследствии эффектом Комптона, не укладывается в рамки волновой теории, согласно которой длина волны излучения не должна изменяться при рассеянии. Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ: 

,где Λ = 2,43·10^–3 нм – так называемая комптоновская длина волны, не зависящая от свойств рассеивающего вещества, а только от угла между падающим и рассеянным излучением.

Рассмотрим упругое столкновение двух частиц – налетающего фотона, обладающего энергией E₀ = hν₀ и импульсом p₀ = hν₀ / c, с покоящимся электроном, энергия покоя которого равна  Фотон, столкнувшись с электроном, изменяет направление движения (рассеивается). Импульс фотона после рассеяния становится равным p = hν / c, а его энергия E = hν < E₀. Уменьшение энергии фотона означает увеличение длины волны. Энергия электрона после столкновения, в соответствии с релятивистской формулой, становится равной  где p_e – приобретенный импульс электрона. Закон сохранения записывается в виде . Закон сохранения импульса  можно переписать в скалярной форме, если воспользоваться теоремой косинусов (см. диаграмму импульсов): Из двух соотношений, выражающих законы сохранения энергии и импульса, после несложных преобразований и исключения величины p_e можно получить mc²(ν₀ – ν) = hν₀ν(1 – cos θ).

После многочисленных преобразований получаем формулу Камптоновско смещения:

32). Модели атома Томсона и Резерфорда. Опыт Резерфорда.

Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит Дж. Дж. Томсону. Согласно этой модели (ещё называлась «булочка с изюмом»), атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10^–10 м, внутри которого около своих положений равновесия колеблются электроны; суммарный отрицательный заряд электронов равен положительному заря­ду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно.

В развитии представлений о строении атома велико значение опытов английского физика Э. Резерфорда по рассеянию альфа-частиц в веществе. На основании своих исследований Резерфорд предложил ядерную (планетарную) модель атома. Исследование заключалось в прохождении альфа частиц сквозь металлическую фольгу. Согласно этой модели, вокруг положительного ядра, имеющего заряд Zе (Z — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер и массу, практически равную массе атома, в области с линейными размерами по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.

В результате оказалось, что большинство альфа частиц проходили или отклонялись на маленькое расстояние. В связи с этим, Резерфорд сделал вывод, что альфа частицы отклонялись лишь под действием положительно заряженных частиц атома и сосредоточены они в малом объёме.

- радиус первой орбиты

33). Спектр атома водорода. Формула Бальмера. Постулаты Бора.

Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко времени создания теории он был хорошо изучен экспериментально. Было известно, что он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона.

Спектральная серия – совокупность спектральных линий, которые в своей последовательности и разделении интенсивности определяют определённую закономерность. Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно. Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Позже аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра.

- общая формула Бальмера

Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... Для инфракрасной серии: серия Пашена (m = 3, n = 4, 5, 6), серия Брекета (m = 4, n = 5, 6, 7) и так далее (серии Порунда и Хэмфри). Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·10¹⁵. Постулаты Бора определили направление развития новой науки – квантовой физики атома.

1-й постулат (постулат стационарных состояний):  атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия E_n. В стационарных состояниях атом не излучает. Для стационарных орбит используется условие квантования момента импульса

2-й постулат (правило частот): при переходе электрона из одного состояния в другое, атом поглощает излучение одного фотона, частота которого равна => hν_nm = E_n – E_m, , где h – постоянная Планка.

36). Соотношение неопределенностей Гейзенберга

Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики. В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, p_у, p_z), причем неопределенности этих величин удовлетворяют условиям т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h..Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т. е. неопределенности этих величии удовлетворяют условию , где  Е —неопределенность энергии некоторого состояния системы, t — промежуток времени, в течение которого оно существует.Пары величин, для которых выполняется принцип неопределённости, называются канонически сопряжёнными. Так, , где А и В – канонически сопряжённые величины.

34). Опыт Франка и Герца

Существование дискретных энергетических уровней атома подтверждается опытом Франка и Герца. В опытах использовалась трубка (рис. 6.9), заполненная парами ртути и три электрода: катод, сетка и анод.

       Электроны ускорялись разностью потенциалов U между катодом и сеткой. Эту разность потенциалов можно было изменять с помощью потенциометра. Между сеткой и анодом было тормозящее поле (метод задерживающих потенциалов).

Определялась зависимость тока через гальванометр от разности потенциалов между катодом и сеткой. В эксперименте была получена зависимость, изображенная на рис. 6.10. Здесь U = 4,86 В – соответствует первому потенциалу возбуждения.

Согласно боровской теории, каждый из атомов ртути может получить лишь вполне определенную энергию, переходя в одно из возбужденных состояний. Поэтому если в атомах действительно существуют стационарные состояния, то электроны, сталкиваясь с атомами ртути, должны терять энергию дискретно, определенными порциями, равными разности энергии соответствующих стационарных состояний атома.

       Из опыта следует, что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возрастает монотонно, его значение проходит через максимум (4,86 В), затем резко уменьшается и возрастает вновь.

       Ближайшим к основному, невозбужденному состоянию атома ртути является возбужденное состояние, отстоящее по шкале энергий на 4,86 В. Пока разность потенциалов между катодом и сеткой меньше 4,86 В, электроны, встречая на своем пути атомы ртути, испытывают с ними только упругие соударения. При  = 4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального состояния в возбужденное. Электроны, потерявшие свою кинетическую энергию, уже не смогут преодолеть тормозящий потенциал и достигнуть анода. Этим и объясняется резкое падение анодного тока при  = 4,86 эВ. При значениях энергии, кратных 4,86, электроны могут испытывать с атомами ртути 2, 3, … неупругих соударения. При этом они полностью теряют свою энергию и не достигают анода, т.е. наблюдается резкое падение анодного тока.

       Таким образом, опыт показал, что электроны передают свою энергию атомам ртути порциями, причем 4,86 эВ – наименьшая возможная порция, которая может быть поглощена атомом ртути в основном энергетическом состоянии. Следовательно, идея Бора о существовании в атомах стационарных состояний блестяще выдержала проверку экспериментом.

       Атомы ртути, получившие при соударении с электронами энергию  , переходят в возбужденное состояние и должны вернуться в основное, излучая при этом, согласно второму постулату Бора, квант света с частотой  . По известному значению  можно вычислить длину волны светового кванта:  . Таким образом, если теория верна, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источником ультрафиолетового излучения с , что действительно обнаружилось в опытах.

       Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но и второй постулат Бора и сделали большой вклад в развитие атомной физики.

35). Гипотеза де Бройля и её экспериментальное подтверждение. Волна де Бройля.

Волны де Бойля - волны, связанные с любыми микрочастицами и отражающие их волновую природу.

Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом.

Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна: , а длина волны: , где p - импульс движущейся частицы, - постоянная Планка. Эти волны и получили название волн де Бройля.

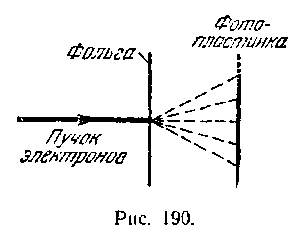
Гипотеза де-Бройля вскоре была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Опыт осуществлялся следующим образом (рис. 190). Пучок электронов, ускоренных разностью потенциалов порядка нескольких десятков киловольт, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Электрон при ударе о фотопластинку оказывает на нее такое же действие, как и фотон. Полученная таким способом электронограмма золота сопоставлена с полученной в аналогичных условиях рентгенограммой алюминия. Сходство обеих картин поразительно.

Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях

дифракционная картина соответствует длине волны, определяемой соотношением (64.1).

Из описанных опытов с несомненностью вытекает, что пучок микрочастиц определенной скорости и направления дает дифракционную картину, подобную картине, получаемой от плоской волны.

37). Волновая функция и её свойства. Её физический смысл.

Волнова́я фу́нкция, или пси-функция  — комплекснозначная функция, используемая в квантовой механике для описаниячистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

где  — координатный базисный вектор, а  — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Физический смысл волновой функции.

В координатном представлении волновая функция  зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности  (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами  в момент времени :.

Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность  того, что частица будет обнаружена в любой области пространства конечного объема :      

38). Уравнение Шредингера для стационарных состояний

Основываясь на основном уравнением нерелятивистской квантовой механики - временное уравнение Шредингера где  - оператор полной энергии частицы (оператор Гамильтона), делаем следующие выводы:

в уравнении  левая часть зависит только от времени, а правая - только от координат. Выполнение этого равенства возможно лишь в том случае, если левая и правая части уравнения равны постоянной величине, обозначим ее буквой  . Таким образом получаем два уравнения - одно для функции  , а другое - для функции  Уравнение  определяет собственные значения и собственные функции оператора полной энергии (гамильтониана) . Следовательно, константа  представляет собой не что иное, как полную энергию квантово-механической системы. Перепишем данное уравнение с учетом вида оператора 

     где  - оператор Лапласа. Полученное уравнение называется уравнением Шредингера для стационарных состояний. Его решения - функции  и соответствующие значения энергии  - определяются конкретным видом потенциальной энергии частицы  . Часто уравнение Шредингера для стационарных состояний записывают в следующей форме

39). Движение свободной частицы

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенци­альная энергия частицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера для стационарных состояний примет вид

Прямой подстановкой можно убедиться в том, что частным решением уравнения полученного является функция (х) = Ае^ikx , где А = const и k = const, с собственным значением энергии  (2)

Функция  представляет собой только координатную часть волновой функции (x, t). Поэтому зависящая от времени волновая функция получится,     (3)

(здесь  и ). Функция (3) представляет собой плоскую монохромати­ческую волну де Бройля. Из выражения (2) следует, что зависимость энергии от импульсаоказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число kможет принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным. Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространстват. е. все положения свободной частицы в пространстве являются равновероятными.

40). Частица в одномерной потенциальной яме

Стационарным состояниям частицы, запертой в потенциальной яме, соответствует дискретный набор длин волн. Поскольку в квантово-механическом случае длина волны λ однозначно связана с импульсом частицы: λ = h / p, а импульс частицы определяет энергию ее движения: E = p² / (2m)(нерелятивистское приближение), то квантованной оказывается и энергия частицы. Квантово-механический расчет приводит к следующему выражению:

 Здесь m – масса частицы, h – постоянная Планка, E₁ = h² / (8mL²) – энергия наинизшего состояния. Следует обратить внимание, что квантово-механическая частица в отличие от классической не может покоиться на дне потенциальной ямы, то есть иметь энергию E₁ = 0. Это противоречило бы соотношению неопределенностей Δx · Δp_x ≥ h

Действительно, у покоящейся частицы импульс строго равен нулю, следовательно, Δp_x = 0. В то же время неопределенность координаты частицы Δx ≈ L. Поэтому произведение Δx · Δp_x у частицы, лежащей на дне потенциальной ямы, должно было бы равняться нулю. Соотношение неопределенностей позволяет сделать оценку минимальной энергии E₁ частицы. Если принять, что в состоянии с минимальной энергией p_x ≈ Δp_x, то для минимальной энергии E₁ получается выражения  . Эта грубая оценка дает правильное по порядку величины значение E₁. Стоячие волны де Бройля, образующиеся при движении частицы в потенциальной яме, это и есть волновые или пси-функции, с помощью которых квантовая механика описывает стационарные состояния микрообъектов. Квадрат модуля |Ψ|² волновой функции определяется как вероятность нахождения частицы в различных точках пространства. В компьютерной модели можно изменять ширину L потенциальной ямы, а также массу m запертой в ней частицы. В левом окне высвечиваются графические изображения волновых функций Ψ(x) или квадратов их модулей |Ψ|² для нескольких стационарных состояний (n = 1–5). В правом окне изображается энергетический спектр частицы, то есть спектр возможных значений ее энергии. Обратите внимание, что энергетические уровни опускаются при увеличении ширины L потенциальной ямы и массы m запертой в ней частицы..

- собственная волновая функция для частицы в одномерной потенциальной яме.