ман для 1ПМ-11 / 2 курс 2011 / лекции / Неперервність функцій / лекция № 13

Міністерство освіти і науки, молоді та спорту України

Горлівський технікум Донецького національного університету

ЛЕКЦІЯ № 13

з теми: «Властивості неперервних функцій на проміжутках..»

Модуль КЗН-02. ПР.О.03.04 Неперервність функцій

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено Розробив викладач

на засіданні циклової Велікодна О. В.

комісії інформаційних технологій

та прикладної математики.

протокол № 1 від 30.08.2011 р.

Голова циклової

комісії ІТ та ПМ І. П. Сошина

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІ

Викладач: Велікодна Ольга Володимирівна

Тема: Властивості неперервних функцій на проміжках.

Мета:

• Дидактична: вивчити властивості неперервних функцій на проміжках, навчитися досліджувати функцію на неперервність та рівномірну неперервність.

• Виховна: виховувати професійно зацікавлену особистість, здатну вільно мислити та логічно висловлювати свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням технологій проблемного та проектного навчання.

Тип: лекція № 13

Вид: лекція – дослідження проблемних питань.

Методи та форми проведення заняття: метод проблемного викладення матеріалу, репродуктивний, дослідницький.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ.

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань:

3. Вивчення нового матеріалу:

• Тема лекції: Властивості неперервних функцій на проміжках.

• Мотивація вивчення матеріалу: вивчити основне поняття математичного аналізу – границі функції в точці, яке дає можливість застосування апарату дослідження у будь – яких сферах прикладання математичних задач.

• План вивчення нового матеріалу: надається в конспекті заняття.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

План лекції № 13.

1. Границя та неперервність композиції функцій.

2. Обмеженість неперервних функцій. Досягнення екстремальних значень.

3. Проміжуточні значення неперервних функцій.

4. Зворотні функції.

5. Неперервність елементарних функцій.

Конспект лекції № 13.

Тема: «Властивості неперервних функцій на проміжутках..»

1. Визначення 1.Якщо ƒ: X→Y та g: Y→Z, то функція z: X→Z називається композицією функцій ƒ та g, чи складною функцією та позначається g ◦ ƒ чи g(ƒ(x)). Тобто (g ◦ ƒ)(х) = g(ƒ(x)).

Теорема. Нехай функція ƒ: X→Y та функція g: Y→Z. Якщо існують скінчені чи нескінчені границі та , то при х → х існує границя складної функції g(ƒ(x)), причому .

Якщо функція g неперервна в точці у, то .

Наслідки. Якщо функція ƒ неперервна в точці х та g неперервна в точці у= ƒ(х), то їх композиція g ◦ ƒ неперервна в точці х.

2. Визначення 2. Функція називається неперервною на множині, якщо вона неперервна в кожній її точці.

Теорема.(Веєрштрасса) Будь – яка неперервна на відрізку функція досягає на ньому своєї верхньої та нижньої граней.

3. Теорема. (Больцано – Коші) Якщо функція ƒ неперервна на відрізку [a, b],

ƒ(а) = А, ƒ(b) = В, то для будь – якого числа С: A ≤ C ≤ B, існує така точка ξ [a, b], що ƒ(ξ) = С.

Наслідки. Якщо функція неперервна на відрізку та на його кінцях приймає значення різних знаків, то на цьому відрізку існує хоча б одна точка, в якій функція дорівнює 0.

4. Визначення 3. Функція, визначена на множині Y = ƒ(X) значень функції ƒ: X→Y, з областю значень X, що ставить у відповідність кожному елементу уY його прообраз {x: ƒ(x) = y}, називається зворотною до ƒ функцією та позначається .

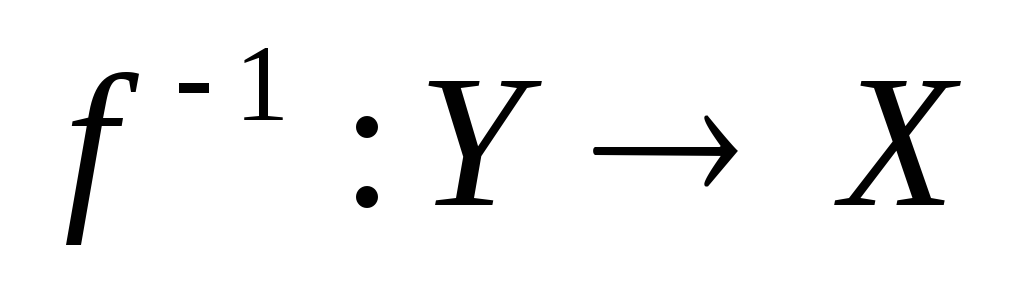Лемма. Якщо функція ƒ строго зростає на множині Х та ƒ(Х) = Y, то зворотна функція є строго зростаючою на множині Y функцією.

Теорема. Якщо функція ƒ строго зростає та неперервна на відрізку [a, b], ƒ(а) = А, ƒ(b) = В, то ƒ([a, b]) = [A, B] та зворотна функція є однозначно строго зростаючою неперервною на відрізку [A, B] функцією.

Теорема. Якщо функція ƒ строго зростає та неперервна на інтервалі (a, b), ƒ(х) = А, ƒ(х) = В, то ƒ((a, b)) = (A, B) та зворотна функція є однозначно строго зростаючою неперервною на інтервалі (A, B) функцією.

5. Теорема. Багаточлен - неперервна на всій числовій осі функція.

Теорема. Раціональна функція , де Р(х) та Q(х) – багаточлени, неперервна у всіх точках числової осі, в яких Q(х) ≠ 0.

6. Основні властивості ступенів а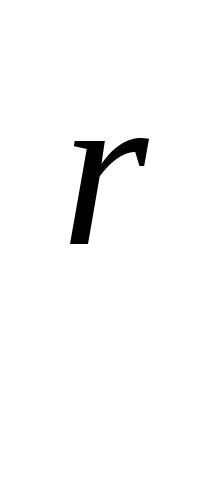, а > 0, с раціональними показниками rQ:

• Нехай . Якщо а > 1, то , а якщо 0 < а < 1, то .

• = .

• ()=.

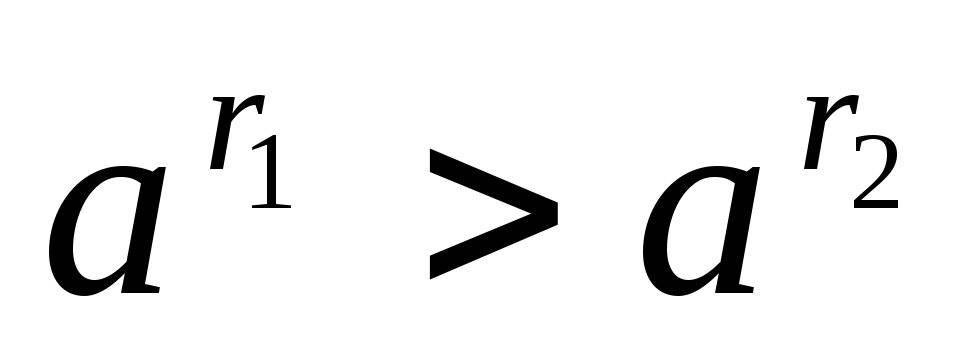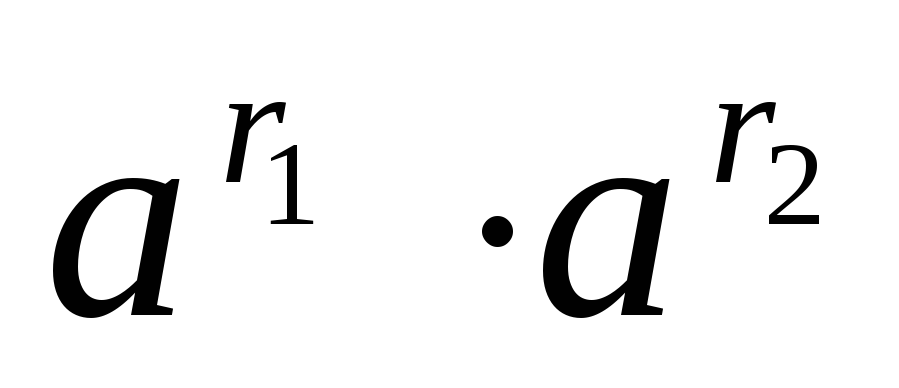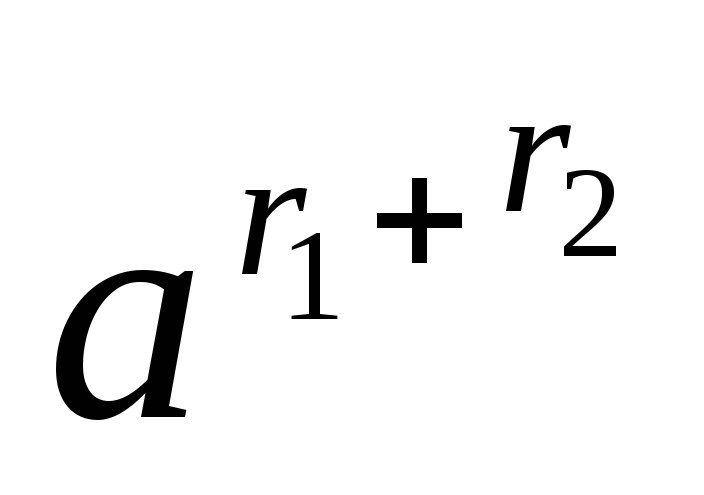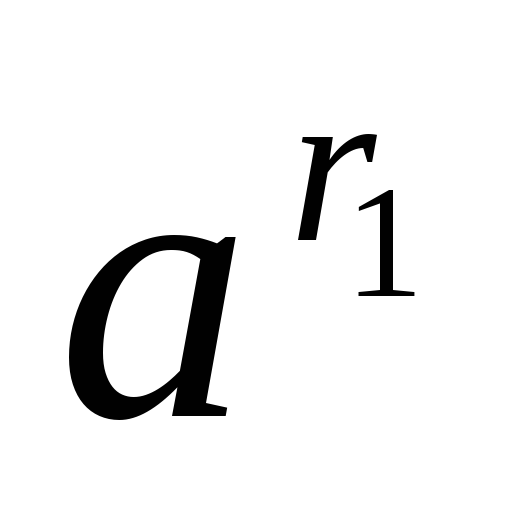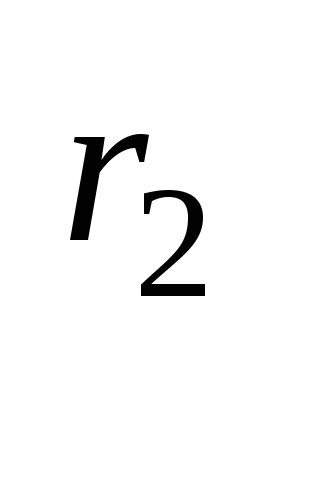• а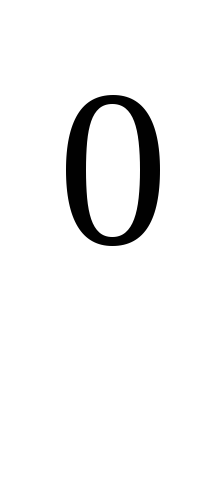= 1.

• а.

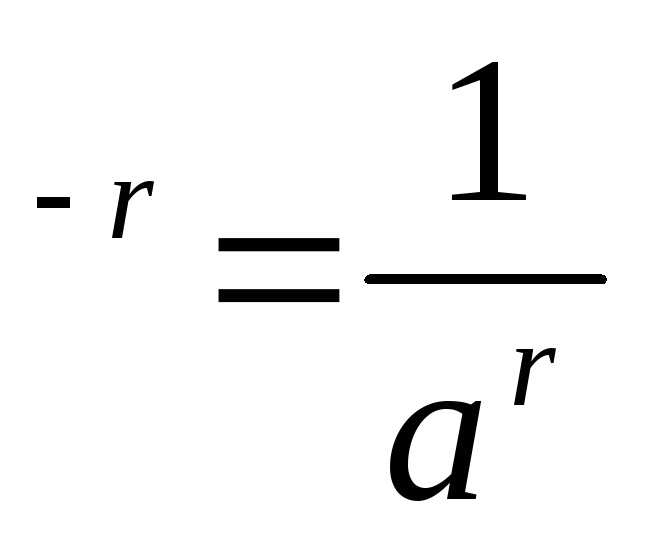Лемма. Для любого а > 0 має місце рівність = = 1.

Лемма. Нехай а > 0, тоді = 1.

Визначення 1. Нехай а > 0 та х R. Визначимо а як границю а по множині раціональних чисел Q, коли r → х, тобто а = . Функція ƒ(х) = а, а > 0, х R, називається показниковою функцією.

Теорема. Показникова функція ƒ(х) = а, а > 0, має наступні властивості:

• Якщо а > 1, вона строго зростає, а якщо 0 < а < 1 – строго спадає на всій числовій осі.

• Для всіх х R та уR має місце рівність: 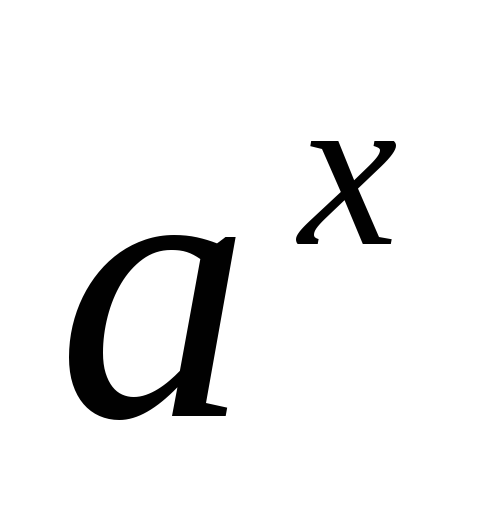а=.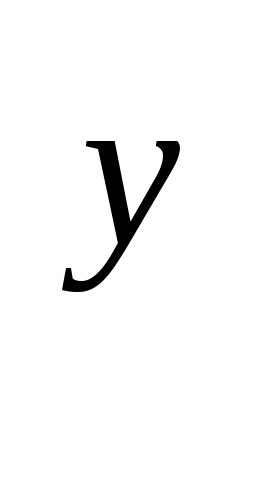

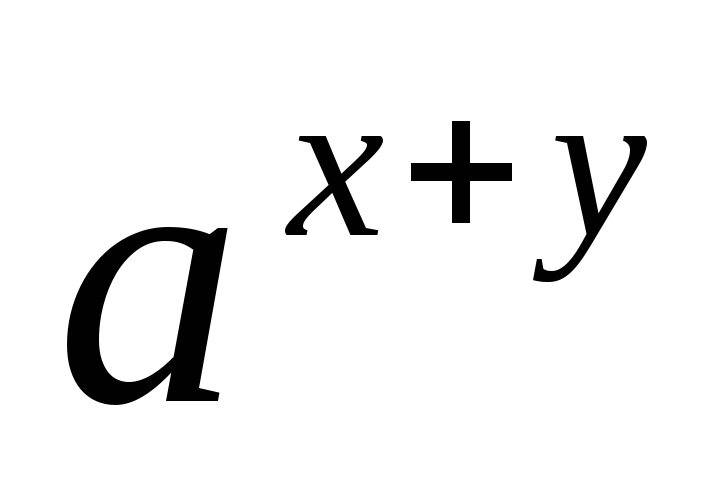• Для всіх х R та уR має місце рівність: ()=.

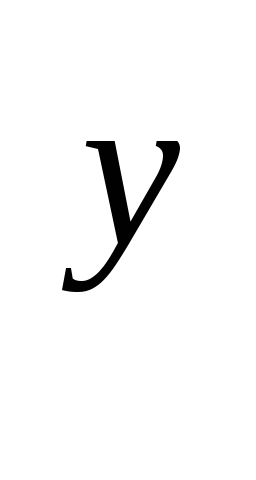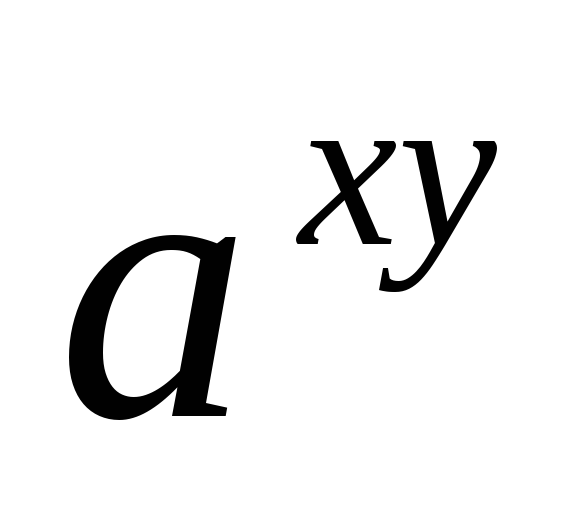• Функція у = а 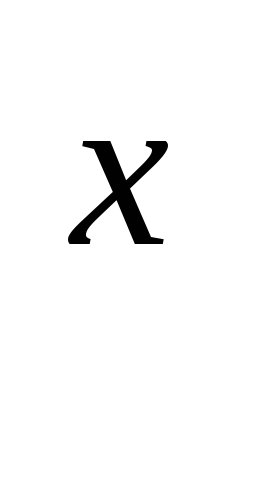неперервна на всій числовій осі.

• Областю значень функції а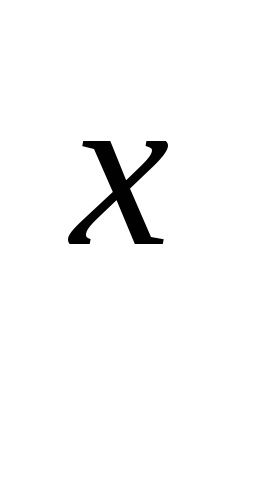є множина всіх додатних чисел, тобто нескінчений інтервал (0, + ∞).

Функція, зворотна до показникової у = а, а > 0, а ≠ 1, називається логарифмічною та позначається . Логарифм визначений для любого додатного числа. Число а називається основою логарифмічної функції у = , логарифмічна функція з основою а = е називається натуральним логарифмом та позначається .

Відповідно до визначення зворотної функції справедлива тотожність а = х.

З властивостей показникової функції маємо такі властивості логарифму:

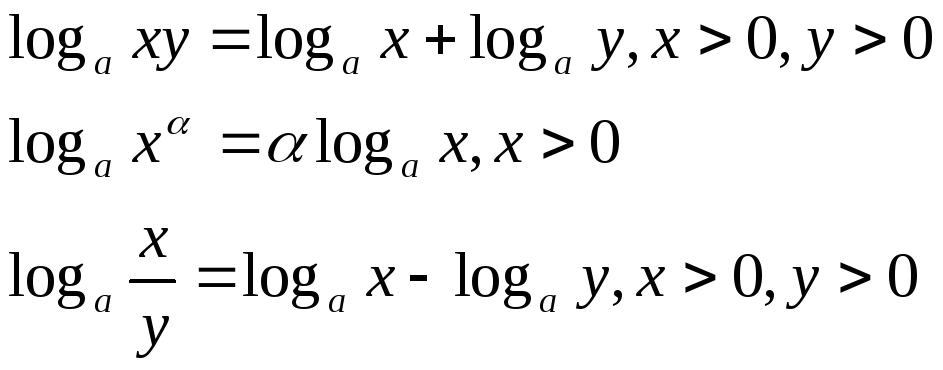
7. Визначення 2. Функція у = х, х > 0, αR називається ступеневою функцією.

Теорема. При будь – якому αR ступенева функція х неперервна при всіх х > 0.

8. Лемма. Для будь – якого дійсного числа х має місце нерівність |sin x| ≤ |x|.

Теорема. Функції у = sin x та у = cos х неперервні на всій числовій осі.

Наслідки. Функції tg х = та ctg х = неперервні у всіх точках числової осі, окрім тих, в яких їх знаменники звертаються в 0 (х ≠ , х ≠ відповідно).

Теорема. Кожна із зворотних тригонометричних функцій у = arcsin х , у = arccos х, у = arctg х , у = arcctg х неперервні в області свого визначення.

Теорема. Кожна елементарна функція неперервна в області свого визначення.