
ман для 1ПМ-11 / 2 курс 2011 / лекции / Неперервність функцій / лекция № 14
.docxМіністерство освіти і науки, молоді та спорту України
Горлівський технікум Донецького національного університету
ЛЕКЦІЯ № 14
з теми: «Рівномірна неперервність функцій на множині.»
Модуль КЗН-02. ПР.О.03.04 Неперервність функцій
Дисципліна: «Математичний аналіз»
Розглянуто та схвалено Розробив викладач
на засіданні циклової циклової комісії ПМ
комісії «Прикладна математика». Велікодна О. В.
протокол № ____ від _______20__ р.
Голова циклової
комісії ПМ І. П. Сошина
ПЛАН ЗАНЯТТЯ
Дата: 15.02.2012 курс: ІІ, група 2ПМ10
Викладач: Велікодна Ольга Володимирівна.
Тема: Рівномірна неперервність функцій на множині.
Мета:
-
Дидактична: повторити поняття елементарної функції, розглянути питання неперервності елементарних функцій, навчитись досліджувати функцію на неперервність та рівномірну неперервність.
-
Виховна: виховувати професійно зацікавлену особистість, здатну вільно мислити та логічно висловлювати свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням технологій проблемного та проектного навчання.
Тип: лекція № 14
Вид: лекція – дослідження проблемних питань.
Методи та форми проведення заняття: метод проблемного викладення матеріалу, репродуктивний, дослідницький.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань:
-
Вивчення нового матеріалу:
-
Тема лекції: Рівномірна неперервність функцій на множині.
-
Мотивація вивчення матеріалу: вивчити основні поняття, пов’язані з неперервністю елементарних функцій та їх застосуванням при розв’язанні прикладних задач.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання: Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989 – том 1, стор. 203, № 19, стор. 208, № 57, 58.
План лекції № 14.
-
Визначення рівномірно неперервної функції.
-
Умови рівномірної неперервності функції на множині. Теорема Кантора.
-
Приклади.
Конспект лекції № 14.
Тема: «Рівномірна неперервність функцій на множині.»
Визначення:
Функція
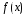 ,
визначена на множині
,
визначена на множині
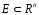 називається
рівномірно неперервною на
називається
рівномірно неперервною на
 ,
якщо для будь – якого
,
якщо для будь – якого
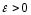 існує таке
існує таке
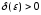 ,
що для будь – яких двох точок
,
що для будь – яких двох точок
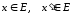 ,
що задовольняють умові
,
що задовольняють умові
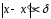 ,
виконано нерівність
,
виконано нерівність
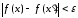 .
.
Якщо
функція рівномірно неперервна на множині
Е, то вона і просто неперервна на Е, тобто
неперервна в кожній точці
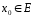 (зворотне
твердження не вірне, так як в цьому
випадку вибір
(зворотне
твердження не вірне, так як в цьому
випадку вибір
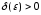 залежить
не тільки від
залежить
не тільки від
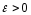 ,
а й від самої точки
,
а й від самої точки
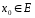 ).
У випадку, коли функція рівномірно
неперервна на множині Е, вибір відповідного
).
У випадку, коли функція рівномірно
неперервна на множині Е, вибір відповідного
 залежить тільки від
залежить тільки від
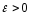 та не залежить від розглянутих точок
множини Е.
та не залежить від розглянутих точок
множини Е.
Приклади.
-
Функція (х) = х рівномірно неперервна на всій числовій осі, так як, якщо задане число > 0, достатньо взяти = , тоді, якщо
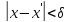 ,
то
,
то
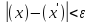 .
. -
Функція
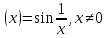 не є рівномірно неперервною на своїй
області визначення, тобто на числовій
осі, з якої видалена точка х = 0. Дійсно,
якщо взяти, наприклад
= 1, то при будь-якому малому
0 знайдуться точки
не є рівномірно неперервною на своїй
області визначення, тобто на числовій
осі, з якої видалена точка х = 0. Дійсно,
якщо взяти, наприклад
= 1, то при будь-якому малому
0 знайдуться точки
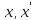 ,
наприклад
,
наприклад
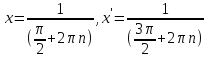 ,
n
– достатньо велике натуральне число,
такі, що
,
n
– достатньо велике натуральне число,
такі, що
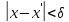 ,
але
,
але
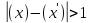
Достатня
умова рівномірної неперервності функції
на інтервалі:
якщо функція
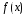 визначена
та має обмежену похідну на інтервалі
визначена
та має обмежену похідну на інтервалі
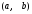 ,
то вона рівномірно неперервна на цьому
інтервалі.
,
то вона рівномірно неперервна на цьому
інтервалі.
Принципове значення має наступна
теорема Кантора:
Функція, неперервна на компакті, рівномірна неперервна.
Наслідки: неперервна на відрізку функція - рівномірно неперервна.
Часто,
найбільш зручним є підхід до поняття
рівномірної неперервності за допомогою
визначення
модулю
неперервності функції:
нехай функція
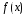 визначена на множині
визначена на множині
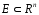 .
Її модулем неперервності
.
Її модулем неперервності
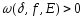 називається функція
називається функція
 .
.
Модуль неперервності є монотонно зростаючою функцією.
Критерій
рівномірної неперервності:
для того, щоб функція
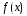 ,
визначена на множині
,
визначена на множині
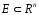 ,
була рівномірно неперервна на цій
множині, необхідно та достатньо, щоб
,
була рівномірно неперервна на цій
множині, необхідно та достатньо, щоб
 ,
,
тобто
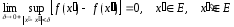
Приклади.
-
Знайдемо модуль неперервності функції
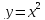 ,
,
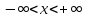 .
Для будь-якого
> 0
та вільного фіксованого
.
Для будь-якого
> 0
та вільного фіксованого
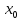 маємо:
маємо:
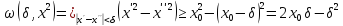 . Ця нерівність є вірною для всіх
. Ця нерівність є вірною для всіх
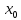 й так як при будь-якому фіксованому
маємо
й так як при будь-якому фіксованому
маємо
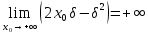 ,
тобто модуль неперервності функції
,
тобто модуль неперервності функції
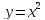 ,
,
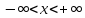 дорівнює +.
дорівнює +. -
Знайдемо модуль неперервності функції
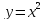 ,
,
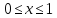 .
Нехай
.
Нехай
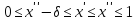 .
Тоді, в силу нерівності
.
Тоді, в силу нерівності
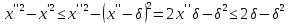 ,
отримаємо, що
,
отримаємо, що
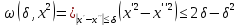 .
Але, якщо взяти
.
Але, якщо взяти
 ,
то
,
то
 .
Отже, маємо, що
.
Отже, маємо, що
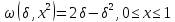 .
. -
На відрізку
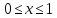 модуль неперервності функції
модуль неперервності функції
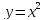 дорівнює
дорівнює
 .
Маємо,
.
Маємо,
 ,
тому функція
,
тому функція
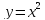 є рівномірно неперервною на відрізку
є рівномірно неперервною на відрізку
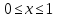 .
. -
На множині
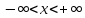 модуль неперервності функції
модуль неперервності функції
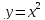 дорівнює
дорівнює
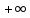 ,
тому ця функція не є рівномірно
неперервною на всій числовій прямій.
,
тому ця функція не є рівномірно
неперервною на всій числовій прямій.
