Ключ до тестового завдання (частина 2).

1а	2а	3б	4в	5а	6в	7а	8а	9б	10б
11б	12в	13б	14в	15а	16г	17в	18в	19а	20а
21в	22в	23г	24в	25в	26в	27а	28б	29а	30а
31г	32а	33в

2. Інструктаж до виконання практичного завдання.

Методичні вказівки.

Границя функції в точці.

Визначення.(по Гейне) Точка а називається границею значень функції ƒ(х), хХ, в точці х, якщо для будь – якої послідовності точок хХ, n = 1,2,…, границя якої є х, тобто , послідовність {ƒ(х)} значень функції ƒ(х) в точках хХ, n = 1,2,…, має своєю границею точку а, тобто .

За допомогою символів визначення записується таким чином:

.

Визначення.(по Коші) Точка а називається границею значень функції ƒ(х), хХ, при х → х, якщо для будь – якої окрестності U(а) точки а існує така окрестність точки х - U(х), що ƒ(Х∩U(х)) U(а).

За допомогою символів визначення записується таким чином:

Видатні границі функції в точці:

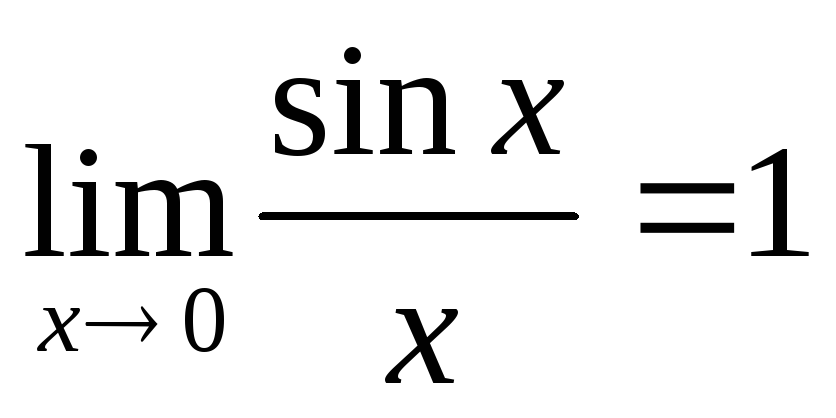• - перша видатна границя.

• ;

• ;

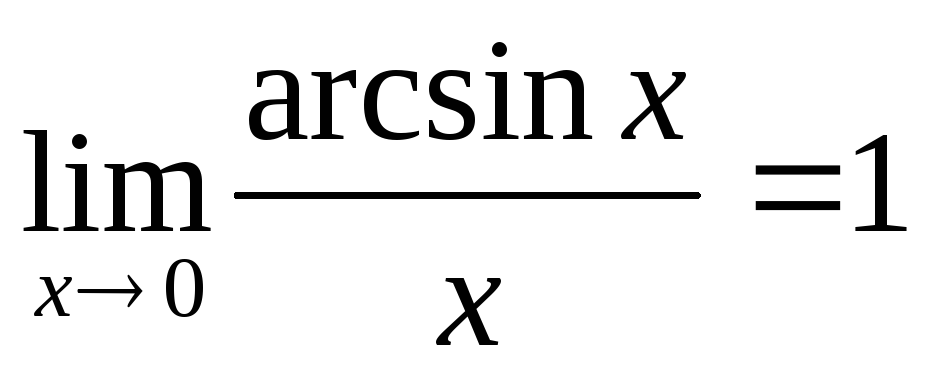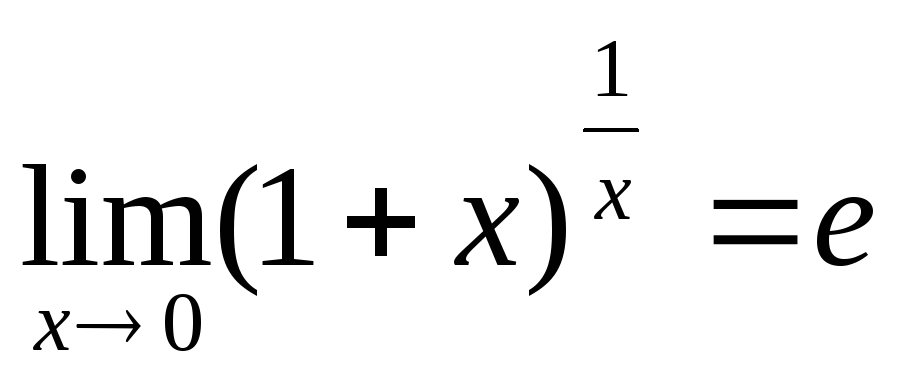• - друга видатна границя.

• ;

• ;

• ;

• .

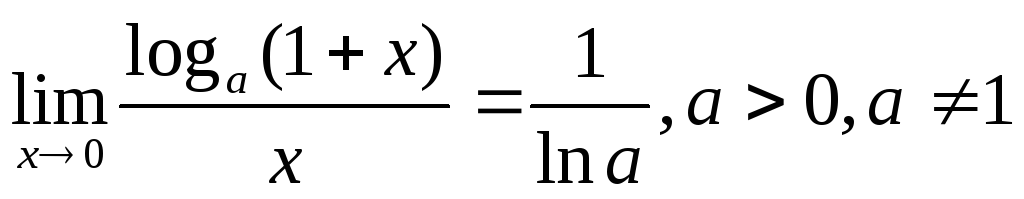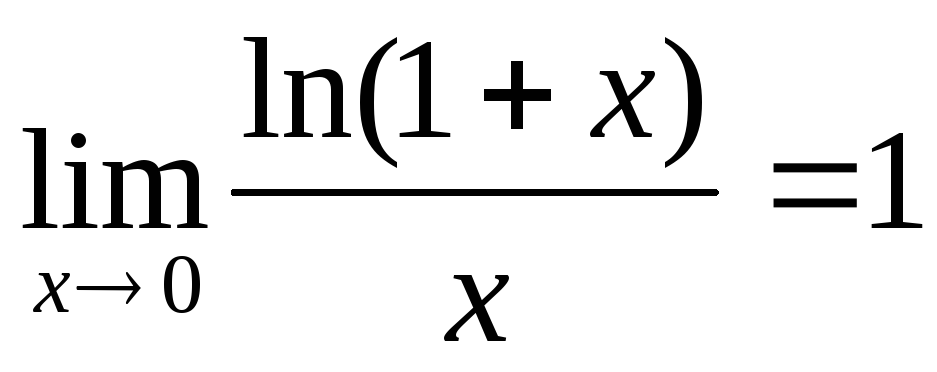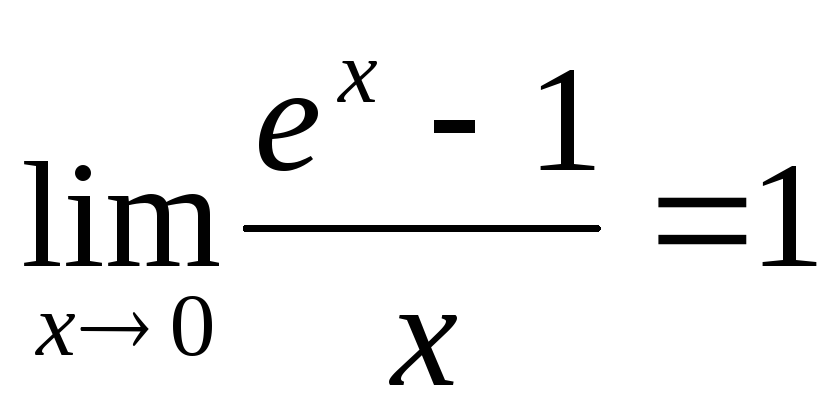Критерій Коші: Для того, щоб функція ƒ(х), хХ, мала в точці х скінчену границю, необхідно та достатньо, щоб для любого існувала така окрестність U(х) точки х, щоб для будь – яких х′Х∩U(х) та х″Х∩U(х) виконувалась нерівність .

За допомогою символів критерій Коші записується таким чином:

.

Однобічні границі.

Визначення. Нехай задана функція ƒ(х), хХ, та х R. Точка а називається границею значень функції ƒ(х) зліва при х → х, якщо вона є границею функції при х → х по множині .

Визначення. Нехай задана функція ƒ(х), хХ, та х R. Точка а називається границею значень функції ƒ(х) справа при х → х, якщо вона є границею функції при х → х по множині .

Однобічні границі функції в точці позначаються так: - границя функції зліва, - границя функції справа. Для позначення границь в 0 та ±∞ використовують позначення: та ; та.

Теорема. Функція ƒ(х), хХ, має границю в точці х= sup = inf,

≠Ø, ≠Ø, тоді та тільки тоді, коли в точці х у функції ƒ(х) існують рівні границі зліва та справа, причому загальне значення цих границь є границею функції ƒ(х) в точці х.

Нескінчені границі.

Якщо границя функції нескінчена, при х → ± ∞, то визначення границі буде:

.

Функція α(х), хХ, називається нескінченно малою при х→ х, якщо .

Зрівняння функцій.

Визначення. Функція ƒ(х) називається функцією, обмеженою відносно функції g(х) в околі точки х, якщо функція φ(х) – обмежена.

Тобто , що означає: |ƒ(х)| ≤ с|g(х)| ().

Якщо ƒ(х) обмежена відносно g(х) в околі точки х, то пишуть ƒ(х) = Ο(g(х)), х → х.

Визначення. Функція ƒ(х) називається функцією того ж порядку, що і функція g(х) в околі точки х, якщо існують такі сталі с> 0 та с > 0, що для всіх х Х∩U виконується нерівність: с ≤ |φ(х)| ≤ с.

Тобто , що означає: с|g(х)| ≤ |ƒ(х)| ≤ с|g(х)|.

Якщо ƒ(х) того ж порядку, що і g(х) в околі точки х, то пишуть ƒ(х) ≈ g(х),

х → х. (ƒ(х) ≈ g(х), х → х) ↔ ( ƒ(х) = Ο(g(х)) та g(х) = Ο(ƒ(х)), х → х).

Визначення. Функція ƒ(х) називається функцією, нескінченно малою відносно функції g(х) в околі точки х, якщо функція φ(х) – нескінченно мала в околі точки х.

Тобто ().

Якщо ƒ(х) нескінченно мала відносно g(х) в околі точки х, то пишуть ƒ(х) = ο(g(х)), х → х.

Визначення. Функція ƒ(х) називається еквівалентною (асимптотично еквівалентною) функції g(х) в околі точки х, якщо ().

Якщо ƒ(х) еквівалентна g(х) в околі точки х, то пишуть ƒ(х) ~ g(х), х → х.

Якщо ƒ(х) = ο(g(х)), х → х та , то функція ƒ(х) називається нескінченно малою більш високого порядку, ніж нескінченно мала g(х).

Ряд еквівалентних функцій:

х ~ sinx ~ tgx ~ arcsinx ~ arctgx ~ ln(1+x) ~ e-1 при х → 0.

Теорема. Для того, щоб функції ƒ(х) та g(х) були еквівалентні при х → х, необхідно та достатньо, щоб ƒ(х) = g(х) + О(g(х)), х → х.

Теорема. Якщо ƒ(х) ~ ƒ(х), g(х) ~ g(х) , х → х та існує , то існує й , причому = .

Приклади виконання практичних завдань.

Обчислити границі функцій в точках.

• .

• 

.

• .

• .

• 

.

• 

.
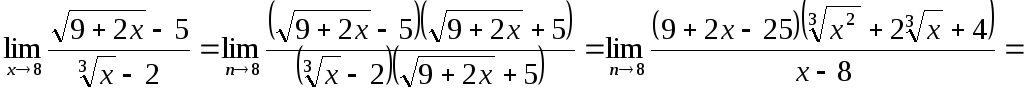
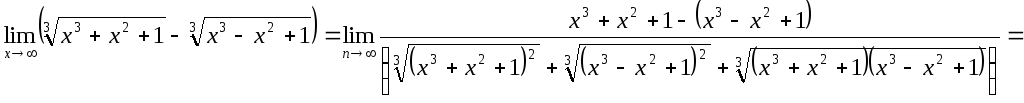
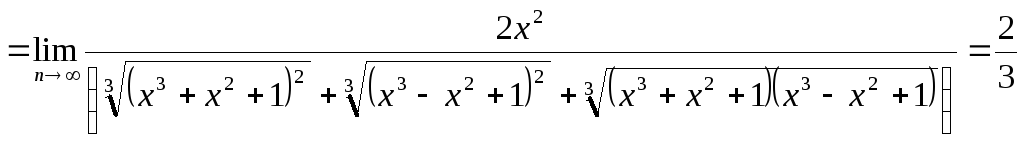
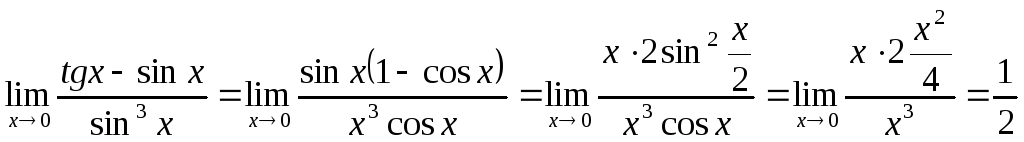
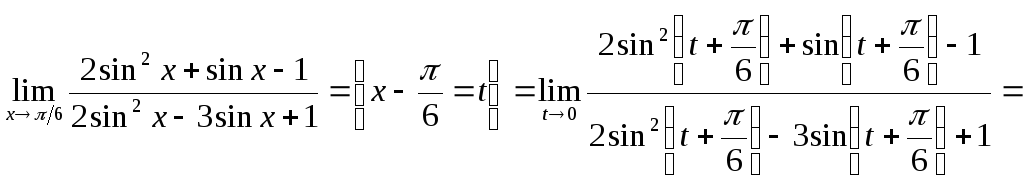
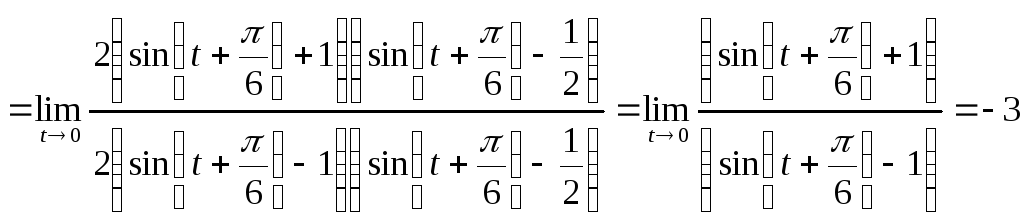
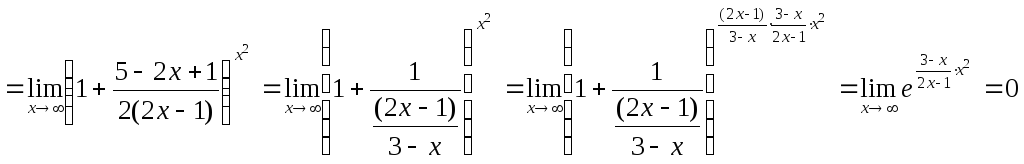