2.3. Метод оберненої матриці

Систему лінійних рівнянь в матричній формі можна записати так:

(2.2)

де А – матриця коефіцієнтів системи рівнянь,

В – матриця – стовпець вільних членів рівнянь,

Х - матриця – стовпець змінних.

Помножимо рівняння (2) на обернену матрицю , отримаємо:

(2.3)

Приклад. Розв’язати систему лінійних рівнянь методом оберненої матриці.

Розв’язок.

1. Знаходимо визначник матриці коефіцієнтів системи рівнянь:

.

Дописуємо два перших стовпця до визначника і знаходимо суму добутків на головних діагоналях та різницю добутків на допоміжних діагоналях:

Визначник матриці коефіцієнтів системи лінійних рівнянь відмінний від нуля, тому існує обернена матриця та існує єдиний розв’язок системи.

2. знаходимо алгебраїчні доповнення кожного елемента матриці коефіцієнтів

,

,

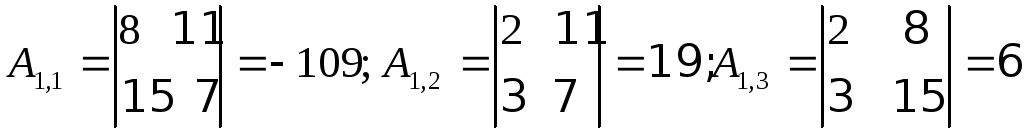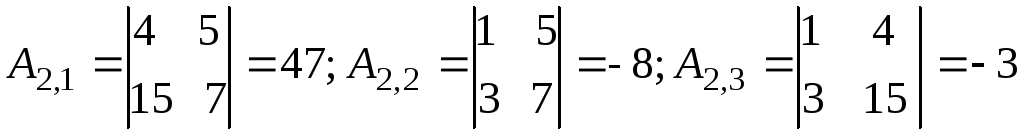3. складаємо матрицю алгебраїчних доповнень:

4. транспонуємо матрицю алгебраїчних доповнень :

.

5. Знаходимо обернену матрицю:

6. знаходимо розв’язок системи рівнянь за формулою (2.3):

.

Відповідь: Х₁= 1, Х₂ = 4, Х₃= -3.

3. Елементи векторної алгебри

Векторними називаються величини, визначені їх числовим значенням та напрямом.

Вектор – відрізок, який має визначену довжину та напрям і позначається або. ТочкаА - початок вектора, точка В - кінець. Довжина вектора називається його модулем або абсолютною величиною і позначається, напрямокАВ визначається променем АВ.

Два вектора тавважаються рівними, якщо рівні їх модулі та співпадають їх напрямки. Вектор не змінюється, якщо його перенести паралельно самому собі в будь яку точку простору. Такий вектор називається ковзним.

Проекцією вектора на вісьОХ називається довжина відрізку А₁В₁ цієї осі між проекціями А₁ та В₁ точок А та В, узята зі знаком “+”, якщо напрямок відрізку А₁В₁ співпадає з напрямком осі ОХ., та зі знаком “-“ , якщо напрямок відрізку А₁В₁ протилежний напрямку осі ОХ . Проекція дорівнює добутку модуля вектора на косинус кута між віссю та вектором:

(3.1)

одиничні вектори координатних осей називаються ортами.

Координати вектора це проекції вектора на осі координат:

.

вектор можна записати через координати так:

.

Якщо вектор заданий точками тато його можна записати так:

.

Кути вектораз осями координат називаються напрямними, а напрямні косинуси визначаються як:

. (3.2)

і відповідають умові:

. (3.3)

модуль вектора дорівнює кореню квадратному зі суми квадратів його координат:

. (3.4)

Приклад. Знайти вектор, який має одиничний модуль і такий напрямок, що і вектор .

Розв’язок.

Одиничний вектор знайдемо за формулою:

, (3.5)

де - довжина вектора.

;

.

Приклад. Знайти напрямні косинуси вектора .

Розв’язок.

Одиничний вектор має модуль, що дорівнює одиниці. Тому з формул (3.2) та (3.4) випливає, що

; ;

.

Відповіді, отримані в задачі 1 і 2, повинні співпадати.

Колінеарні вектори – паралельні одній і тій же прямій, а їх координати відповідають умовам:

. (3.6)

Компланарні вектори – паралельні одній і тій же площині.

Протилежні вектори два колінеарних вектора однакових за модулем та протилежно спрямовані.