тимс - Лекції / закон больших чисел / Лекція 1.3

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 12

з теми: «ЛЕМА ЧЕБИШЕВА. НЕРІВНІСТЬ ЧЕБИШЕВА. ПРИКЛАДИ.»

Модуль КЗН-02. ПР.О.09.03 Закон великих чисел

Дисципліна: «Теорія ймовірностей та математична статистика»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Лема Чебишева. Нерівність Чебишева. Приклади.

Мета:

• Дидактична: ознайомитись з основною теоретичною базою теорії ймовірності – сукупністю теорем та фактів, що складають закон великих чисел. Розглянути практичний зміст закону великих чисел та його важливу роль для теоретичного обґрунтування методів математичної статистики.

• Виховна: створити ситуацію , що спонукає ставити запитання, обґрунтовувати правильність висновків теорії ймовірності в реальному житті.

• Методична: вдосконалити методику проведення лекційного заняття.

Тип: лекція № 12.

Вид: лекція – діалог.

Методи та форми проведення заняття: мовний, наглядний, дослідницький, індуктивний, проблемно – пошуковий, методи усного контролю знань.

Науково-методичне забезпечення:

1. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2002.

2. Гмурман В. Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 1977.

3. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1979.

4. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. Учебное пособие для вузов. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2002.

5. Медведева М. И., Новожилова Е. Г. Теория вероятностей и математическая статистика с применением информационных технологий: Учеб. пособие. – Донецк: ДонНУ, 2002.

Між предметні зв’язки:

• Дисципліни, що забезпечують – дискретна математика, математичний аналіз.

• Дисципліни, що забезпечуються – моделювання виробничих та економічних процесів, математична економіка.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань:

• Дати визначення випадкової величини. Визначити види випадкових величин. Навести приклади.

• Визначити закон розподілу дискретної випадкової величини. Навести приклади.

• Визначити щільність розподілу неперервної випадкової величини.

• Визначити основні числові характеристики випадкових величин: математичне сподівання, дисперсію, середнє квадратичне відхилення. Яку інформацію несуть ці числові характеристики про випадкову величину?

• Функція розподілу випадкової величини: дискретної та неперервної. Властивості функції розподілу.

3. Вивчення нового матеріалу:

• Тема лекції: Лема Чебишева. Нерівність Чебишева. Приклади.

• Мотивація вивчення матеріалу: Як вважається, неможливо передбачити випадок, яке значення прийме випадкова величина в залежності від результату випробування. Звичайно, якщо ми маємо такі обмежені відомості про кожну випадкову величину, то про добуток чи суму деякого числа випадкових величин взагалі складно зробити висновок. Закон великих чисел пояснює, що таке ставлення до випадку невірне, причому пояснення ґрунтується на життєвому досвіді та наукових фактах. Закон великих чисел доводить, що співвідношення між математичними символами відповідає співвідношенням між реальними речами.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу: конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 12.

Тема: «ЛЕМА ЧЕБИШЕВА. НЕРІВНІСТЬ ЧЕБИШЕВА. ПРИКЛАДИ.»

План лекції № 12.

1. Лема Чебишева. Приклади.

2. Нерівність Чебишева. Приклади.

1. Під законом великих чисел розуміють загальний принцип, сформульований академіком А.Н. Колмогоровим:

Сукупна дія великого числа випадкових факторів призводить до результату, майже не залежному від випадку. Це означає, що при великому числі випадкових величин їх середній результат припиняє бути випадковим і може бути передвіщений з великим ступенем визначеності.

Закон великих чисел визначає ряд теорем, в яких визначається факт наближення середніх характеристик великого числа випробувань к деяким визначеним постійним.

Перед тим, як перейти до цих теорем, роздивимось лему і нерівність Чебишева.

Теорема (лема Чебишева):

Якщо випадкова величина Х приймає тільки не від'ємні значення і має математичне чекання, то для будь-якого позитивного числа А вірна нерівність:

Доведення:

Роздивимось дискретну випадкову величину Х.

до того ж

, де р₁, ... , р_п – відповідні імовірності.

Відкинемо перші k не від’ємних значень, отримаємо

оскільки , то

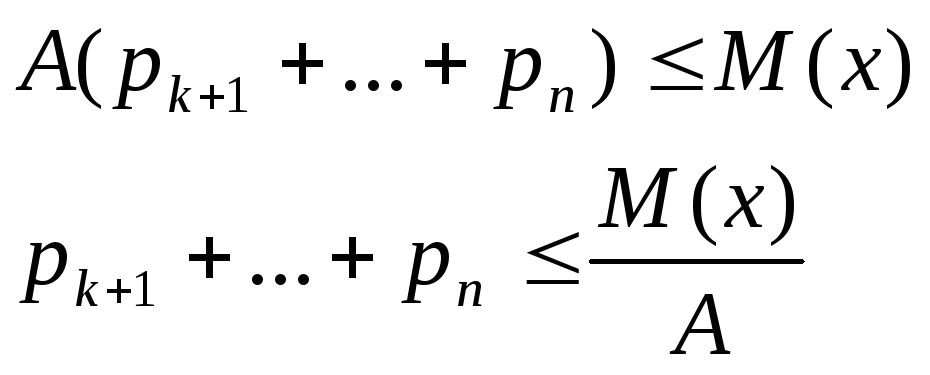
Сума імовірностей .

Значить, . Оскільки події X>A і X≤A – протилежні, то

Лема Чебишева застосовна до будь-яких невід’ємних випадкових величин.

Приклад:

Середня кількість викликів, що поступають на комутатор заводу на протязі години, дорівнює 300. Оцінити імовірність того, що на протязі наступної години число викликів на комутатор: а) перевищить 400; буде не більше 500.

Рішення:

Дано: М(х) =300.

а) За формулою леми , тобто p≤0.75 – не більше 0.75.

б) - не менше 0.4.

Приклад:

Сума всіх внесків у відділення банку складає 2 млн. карбованців, а імовірність того, що випадково взятий внесок не перевищить 10 тис. карбованців, дорівнює 0.6. Що можна сказати про число вкладників.

Рішення:

Нехай Х – розмір випадково взятого внеску, п – число всіх внесків. Тоді, середній розмір внеску По нерівності .

За умовою, , тобто число вкладників не перевищує 500.

2. Нерівність Чебишева.

Теорема:

Для будь-якої випадкової величини, що має математичне чекання і дисперсію, справедлива нерівність Чебишева:

, де а= М(х), ε>0.

Доведення:

Застосуємо лему Чебишева до випадкової величини , де . Тоді .

Оскільки , то , оскільки

Події і - протилежні, і .

Нерівність Чебишева застосовна для будь-яких випадкових величин: у вигляді - встановлює верхню границю, а у вигляді - нижню границю події, що роздивляються.

Для деяких випадкових величин нерівність Чебишева має вид:

а) для випадкової величини Х=т , розподіленої по біноміальному закону з і дисперсією :

.

б) Для частості події в п незалежних випробуваннях, в кожному з яких вона може відбутися з одною і тою ж імовірністю і дисперсією

.

Приклад:

Середня витрата води на тваринницькій фермі складає 1000 л на день, а середнє квадратичне відхилення цієї випадкової величини не перевищує 200л. Оцінити імовірність того, що витрати води на фермі вбудь-який вибраний день не перевершить 2000л, використовуючи: а) нерівність Чебишева; б) лему Чебишева.

ішення:

а) Нехай Х – витрати води на тваринницькій фермі. За умовою М(х)=1000. Тоді, по лемі Чебишева , тобто не менше 0.5.

б) ; - симетричні відносно М(х)=1000, то застосуємо нерівність Чебишева .

- не менше 0.96 (уточнення).

Приклад:

Імовірність виходу з автомату стандартної деталі дорівнює 0.96. Оцінити за допомогою нерівності Чебишева імовірність того, що число бракованих серед 2000 деталей знаходиться в границях від 60 до 100 включно. Уточнити імовірність тої ж події за допомогою інтегральної теореми Муавра-Лапласа. Пояснити різницю отриманих результатів.

Рішення:

За умовою р=1-0.96=0.4 – імовірність того, що деталь бракована.

Число бракованих деталей Х=т має біноміальний закон розподілу, а його границі від 60 до 100 симетричні відносно математичного чекання

Значить, не менш, ніж 0.808.

По інтегральній теоремі Муавра-Лапласа

Отриманий результат Р=0.979 не суперечить оцінці Р≥0.808.

Різниця в тому, що нерівність Чебишева дало лише нижню границю імовірності шуканої події, а інтегральна теорема Муавра-Лапласа дала точну оцінку самої імовірності Р.