
тимс - Лекції / закон больших чисел / Лекція 1.3
.3.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ЛЕКЦІЯ № 14
з теми: «ТЕОРЕМА БЕРНУЛЛІ. ЦЕНТРАЛЬНА ГРАНИЧНА ТЕОРЕМА»
Модуль КЗН-02. ПР.О.09.03 Закон великих чисел
Дисципліна: «Теорія ймовірностей та математична статистика»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики.
Протокол № ____ від _______20__ р.
Голова циклової комісії ПМ Велікодна О. В.
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Теорема Бернуллі. Центральна гранична теорема.
Мета:
-
Дидактична: ознайомитись з основною теоретичною базою теорії ймовірності – сукупністю теорем та фактів, що складають закон великих чисел. Розглянути практичний зміст закону великих чисел та його важливу роль для теоретичного обґрунтування методів математичної статистики.
-
Виховна: створити ситуацію , що спонукає ставити запитання, обґрунтовувати правильність висновків теорії ймовірності в реальному житті.
-
Методична: вдосконалити методику проведення лекційного заняття.
Тип: лекція № 14.
Вид: лекція – діалог.
Методи та форми проведення заняття: мовний, наглядний, індуктивний, методи усного контролю знань.
Науково-методичне забезпечення:
-
Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2002.
-
Гмурман В. Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 1977.
-
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1979.
-
Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. Учебное пособие для вузов. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2002.
-
Медведева М. И., Новожилова Е. Г. Теория вероятностей и математическая статистика с применением информационных технологий: Учеб. пособие. – Донецк: ДонНУ, 2002.
Між предметні зв’язки:
-
Дисципліни, що забезпечують – дискретна математика, математичний аналіз.
-
Дисципліни, що забезпечуються – моделювання виробничих та економічних процесів, математична економіка.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань:
-
Дати визначення випадкової величини. Визначити види випадкових величин. Навести приклади.
-
Визначити закон розподілу дискретної випадкової величини. Навести приклади.
-
Визначити щільність розподілу неперервної випадкової величини.
-
Визначити основні числові характеристики випадкових величин: математичне сподівання, дисперсію, середнє квадратичне відхилення. Яку інформацію несуть ці числові характеристики про випадкову величину?
-
Функція розподілу випадкової величини: дискретної та неперервної. Властивості функції розподілу.
-
Визначити лему та нерівність Чебишева для двох випадків. Пояснити практичний зміст цих тверджень.
-
Визначити теорему Чебишева. Навести приклади її практичного застосування.
-
Вивчення нового матеріалу:
-
Тема лекції: Теорема Бернуллі. Центральна гранична теорема.
-
Мотивація вивчення матеріалу: Як вважається, неможливо передбачити випадок, яке значення прийме випадкова величина в залежності від результату випробування. Звичайно, якщо ми маємо такі обмежені відомості про кожну випадкову величину, то про добуток чи суму деякого числа випадкових величин взагалі складно зробити висновок. Закон великих чисел пояснює, що таке ставлення до випадку невірне, причому пояснення ґрунтується на життєвому досвіді та наукових фактах. Закон великих чисел доводить, що співвідношення між математичними символами відповідає співвідношенням між реальними речами.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу: конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
Конспект лекції № 14.
Тема: «ТЕОРЕМА БЕРНУЛЛІ. ЦЕНТРАЛЬНА ГРАНИЧНА ТЕОРЕМА.»
План лекції № 14.
-
Теорема Бернуллі, наслідки.
-
Приклади.
-
Центральна гранична теорема – теорема Ляпунова.
-
Наслідки теореми Ляпунова.
-
Теорема Бернуллі.
Частість події в п повторних незалежних випробуваннях, в кожному з яких вона може відбутися з одною і тою ж імовірністю р, при необмеженому збільшенні числа п збігається по імовірності до імовірності р цієї події в окремому випробуванні:
![]() або
або
![]() .
.
Узагальненням теореми Бернуллі є теорема Пуассона, коли імовірності події в кожному випробуванні різні.
Теорема Пуассона:
Частість
події в п
повторних випробуваннях, в кожному з
яких вона може відбутися відповідно з
імовірностями р1,
р2,
... рп
при необмеженому збільшенні числа п
збігається по імовірності до середньої
арифметичної імовірностей події в
окремих випробуваннях, тобто
![]() або
або
 .
.
Теорема
Пуассона випливає з теореми Чебишева,
якщо випадкові величини Х1,
..., Хп
мають закон розподілу
![]() ,
тоді
,
тоді
![]() дисперсія
дисперсія
![]() -
обмежені єдиним числом.
-
обмежені єдиним числом.
Важлива роль закону великих чисел в теоретичному обґрунтуванні методів математичної статистики і її додатків обумовила проведення ряду випробувань, спрямованих на вивчення загальних умов застосовності цього закону до послідовності випадкових чисел. Наприклад, дослідження зміни температури в деякій місцевості на протязі року.
При деяких умовах сукупна дія випадкових величин призводить до нормального закону розподілу.
Теорема Ляпунова:
Якщо
Х1,
Х2,
..., Хп
– незалежні випадкові величини, у кожної
з яких існує математичне чекання
![]() і
і
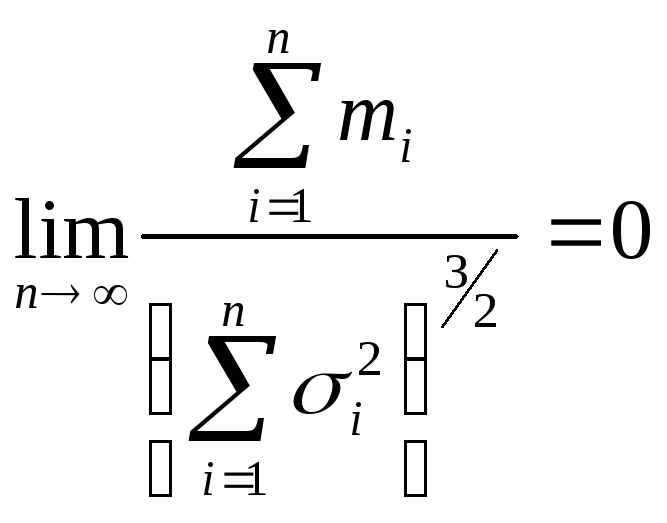 ,
то закон розподілу суми
,
то закон розподілу суми
![]() при п→∞
не обмежено наближає до нормального
закону з математичним чеканням
при п→∞
не обмежено наближає до нормального
закону з математичним чеканням
![]() і дисперсією
і дисперсією
![]() .
.
Наслідок:
Якщо
Х1,
Х2,
..., Хп
– незалежні випадкові величини, у яких
існують рівні математичні чекання
![]() ,
то закон розподілу суми
,
то закон розподілу суми
![]() при п→∞
необмежено наближає до нормального
закону.
при п→∞
необмежено наближає до нормального
закону.
-
Рішення вправ:
Стор. 234: №6.9; 6.10; 6.11; 6.12.
№6.9
Середня зміна курсу акцій компанії на протязі одних біржових торгів складає 0.3%. Оцінити імовірність того, що на найближчих торгах курс зміниться більш ніж на 3%. (нерівність Чебишева).
№6.10
Відділення банку обслуговує в середньому 100 клієнтів на день. Оцінити імовірність того, що сьогодні у відділенні банку буде обслуговано: а) не більше 200 клієнтів; б) більше 150 клієнтів (нерівність Маркова).
№6.11
Електростанція обслуговує мережу на 1600 електроламп, імовірність увімкнення кожної з яких ввечері складає 0.9. Оцінити за допомогою нерівності Чебишева імовірність того, що число ламп, увімкнених в мережу ввечері, відрізняється від свого математичного чекання не більш ніж на 100 (по модулю). Знайти імовірність тієї ж події, застосовуючи наслідок з інтегральної теореми Муавра-Лапласа.
-
Закон великих чисел встановлює факт наближення середньої великого числа випадкових величин до визначених сталих. Але цим не обмежені закономірності, що виникають внаслідок сукупної дії випадкових величин. При деяких умовах сукупна дія випадкових величин призводить до нормального закону розподілу.
Центральна гранична теорема – це група теорем, що встановлюють умови, за яких виникає нормальний закон розподілу. Серед них найважливіше місце займає теорема Ляпунова:
Якщо
Х1, Х2, …, Хn – незалежні випадкові
величини, у кожної з яких існує математичне
сподівання
![]() ,
дисперсія
,
дисперсія
![]() ,
абсолютний центральний момент третього
порядку
,
абсолютний центральний момент третього
порядку
![]() та
та
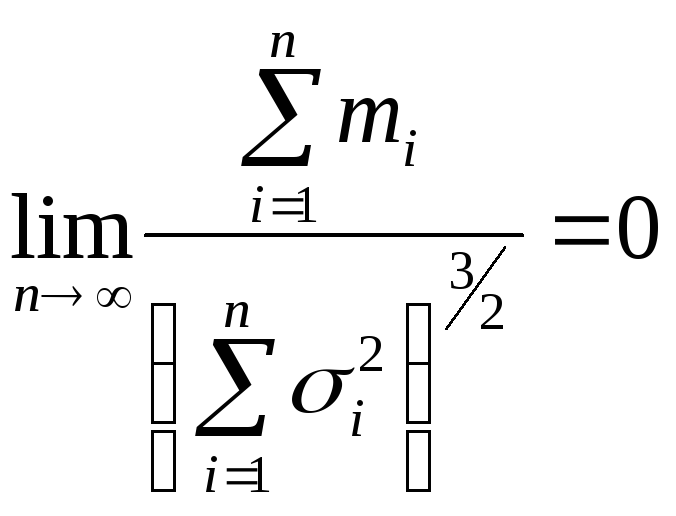 ,
то закон розподілу суми
,
то закон розподілу суми
![]() при
при
![]() необмежено
наближається до нормального з математичним
сподіванням
необмежено
наближається до нормального з математичним
сподіванням
![]() та дисперсією
та дисперсією
![]() .
.
Необмежене наближення до нормального закону розподілу означає, що
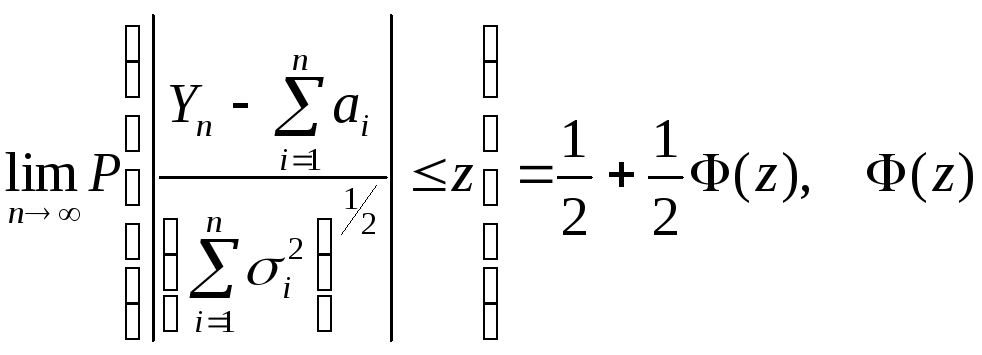 -
функція Лапласа. Кожний окремий доданок
у
-
функція Лапласа. Кожний окремий доданок
у
![]() повинен добігати 0 при збільшені числа
доданків. Наприклад, якщо витрати
електрики для побутових нужд в кожній
оселі багатоквартирного будинку можна
представити у вигляді n різних випадкових
величин, серед яких немає таких, що
виділяються серед інших, то на основі
теорії Ляпунова можна вважати , що
витрати електрики всього дому нормально
розподілені.
повинен добігати 0 при збільшені числа
доданків. Наприклад, якщо витрати
електрики для побутових нужд в кожній
оселі багатоквартирного будинку можна
представити у вигляді n різних випадкових
величин, серед яких немає таких, що
виділяються серед інших, то на основі
теорії Ляпунова можна вважати , що
витрати електрики всього дому нормально
розподілені.
-
Наслідки теореми Ляпунова: Якщо Х1, Х2, …, Хn – незалежні випадкові величини, у яких існують рівні математичні сподівання
 ,
дисперсія
,
дисперсія
 ,
абсолютний центральний момент третього
порядку
,
абсолютний центральний момент третього
порядку
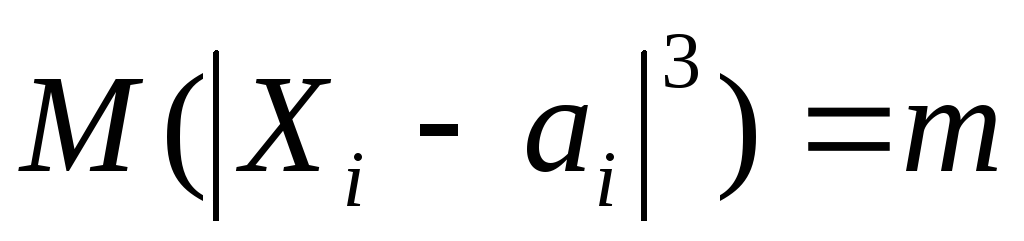 ,
то закон розподілу суми
,
то закон розподілу суми
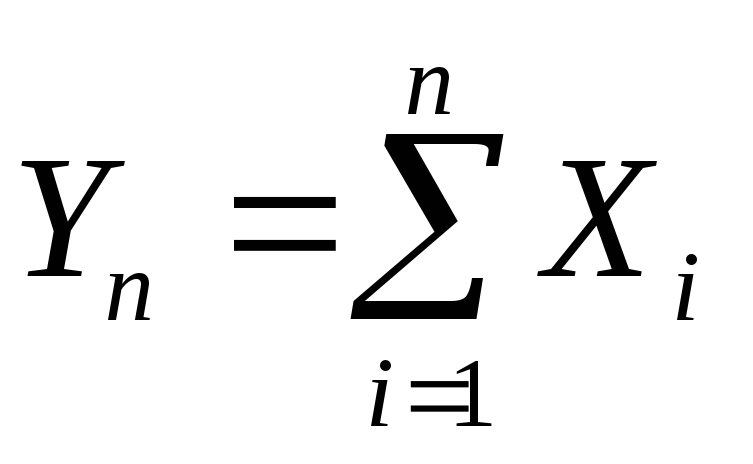 при
при
 необмежено
наближається до нормального з математичним
сподіванням
необмежено
наближається до нормального з математичним
сподіванням
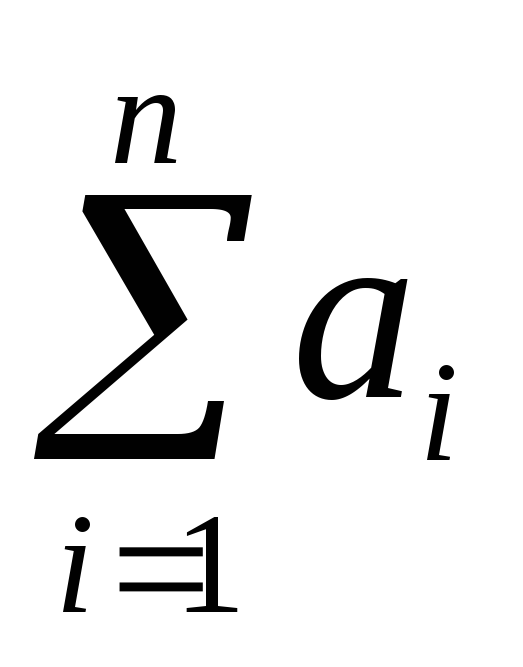 та дисперсією
та дисперсією
 .
На основі наслідків центральної
граничної теореми можна довести локальну
та інтегральну теореми Муавра – Лапласа.
Спираючись на центральну граничну
теорему, можна стверджувати, що випадкові
величини, що мають основні закони
розподілу – біноміальний, Пуассона,
гіпергеометричний при необмеженому
зростанні n асимптотично нормально
розподілені.
.
На основі наслідків центральної
граничної теореми можна довести локальну
та інтегральну теореми Муавра – Лапласа.
Спираючись на центральну граничну
теорему, можна стверджувати, що випадкові
величини, що мають основні закони
розподілу – біноміальний, Пуассона,
гіпергеометричний при необмеженому
зростанні n асимптотично нормально
розподілені.
