тимс - Лекції / закон больших чисел / Лекція 1.3

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 13

з теми: «ТЕОРЕМА ЧЕБИШЕВА. ПРИКЛАДИ.»

Модуль КЗН-02. ПР.О.09.03 Закон великих чисел

Дисципліна: «Теорія ймовірностей та математична статистика»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Теорема Чебишева. Приклади.

Мета:

• Дидактична: ознайомитись з основною теоретичною базою теорії ймовірності – сукупністю теорем та фактів, що складають закон великих чисел. Розглянути практичний зміст закону великих чисел та його важливу роль для теоретичного обґрунтування методів математичної статистики.

• Виховна: створити ситуацію , що спонукає ставити запитання, обґрунтовувати правильність висновків теорії ймовірності в реальному житті.

• Методична: вдосконалити методику проведення лекційного заняття.

Тип: лекція № 13.

Вид: лекція – діалог.

Методи та форми проведення заняття: мовний, наглядний, індуктивний, проблемно – пошуковий, методи усного контролю знань.

Науково-методичне забезпечення:

1. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2002.

2. Гмурман В. Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 1977.

3. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1979.

4. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. Учебное пособие для вузов. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2002.

5. Медведева М. И., Новожилова Е. Г. Теория вероятностей и математическая статистика с применением информационных технологий: Учеб. пособие. – Донецк: ДонНУ, 2002.

Між предметні зв’язки:

• Дисципліни, що забезпечують – дискретна математика, математичний аналіз.

• Дисципліни, що забезпечуються – моделювання виробничих та економічних процесів, математична економіка.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань:

• Дати визначення випадкової величини. Визначити види випадкових величин. Навести приклади.

• Визначити закон розподілу дискретної випадкової величини. Навести приклади.

• Визначити щільність розподілу неперервної випадкової величини.

• Визначити основні числові характеристики випадкових величин: математичне сподівання, дисперсію, середнє квадратичне відхилення. Яку інформацію несуть ці числові характеристики про випадкову величину?

• Функція розподілу випадкової величини: дискретної та неперервної. Властивості функції розподілу.

• Визначити лему та нерівність Чебишева для двох випадків. Пояснити практичний зміст цих тверджень.

3. Вивчення нового матеріалу:

• Тема лекції: Теорема Чебишева. Приклади.

• Мотивація вивчення матеріалу: Як вважається, неможливо передбачити випадок, яке значення прийме випадкова величина в залежності від результату випробування. Звичайно, якщо ми маємо такі обмежені відомості про кожну випадкову величину, то про добуток чи суму деякого числа випадкових величин взагалі складно зробити висновок. Закон великих чисел пояснює, що таке ставлення до випадку невірне, причому пояснення ґрунтується на життєвому досвіді та наукових фактах. Закон великих чисел доводить, що співвідношення між математичними символами відповідає співвідношенням між реальними речами.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу: конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 13.

Тема: «ТЕОРЕМА ЧЕБИШЕВА. ПРИКЛАДИ.»

План лекції № 13.

1. Теорема Чебишева, наслідки.

2. Приклади.

1. Теорема Чебишева:

Якщо дисперсії п незалежних величин Х₁, Х₂, ... , Х_п обмежені одною і тою ж постійною, то при необмеженому збільшенні числа п середня арифметична випадкових величин сходиться по імовірності до середньої арифметичної їх математичних чекань а₁, а₂, ... , а_п тобто

, або

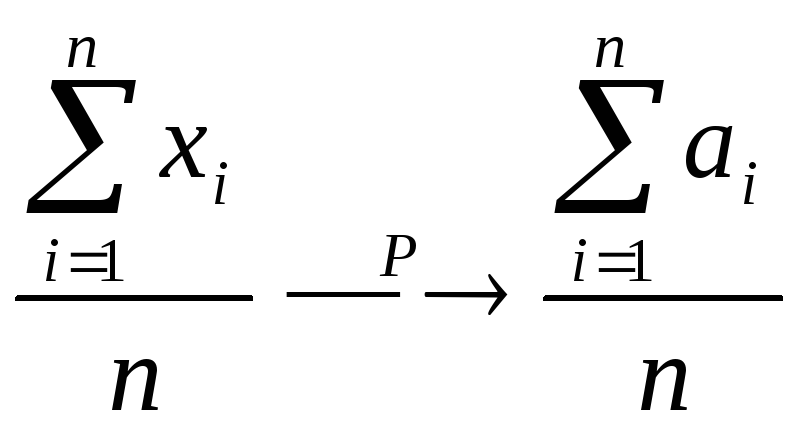
Доведення:

За умовою

.

Застосуємо нерівність Чебишева: для величини , її математичне чекання

, дисперсія .

.

Перейдемо до

Смисл „збіжність по імовірності”: 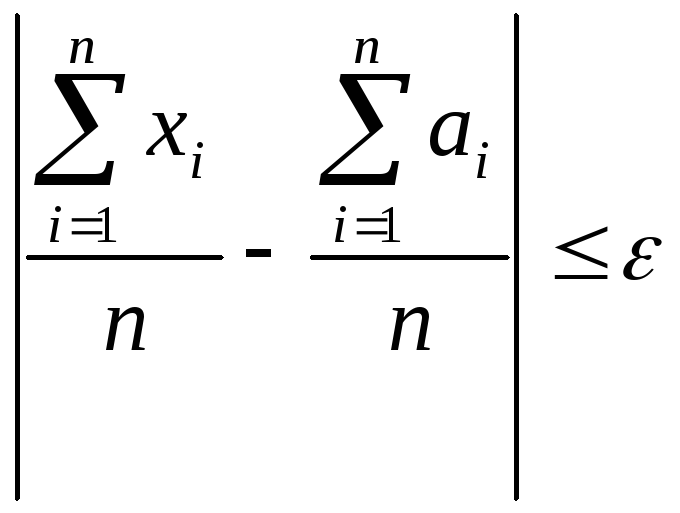і → до 1 відбудеться у гнітючій кількості випадків.

З теореми Чебишева випливає, що при великому числі п випадкових величин Х₁, Х₂, ..., Х_п величина 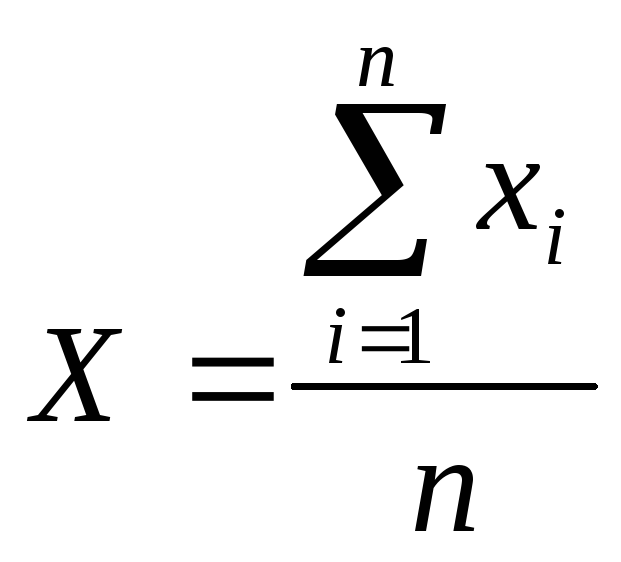перестає бути випадковою, оскільки дуже мало відрізняється від величини .

Наслідок:

Якщо незалежні випадкові величини Х₁, Х₂, ..., Х_п мають однакові математичні чекання, рівні а; їх дисперсії обмежені одною і тою ж постійною, то

або

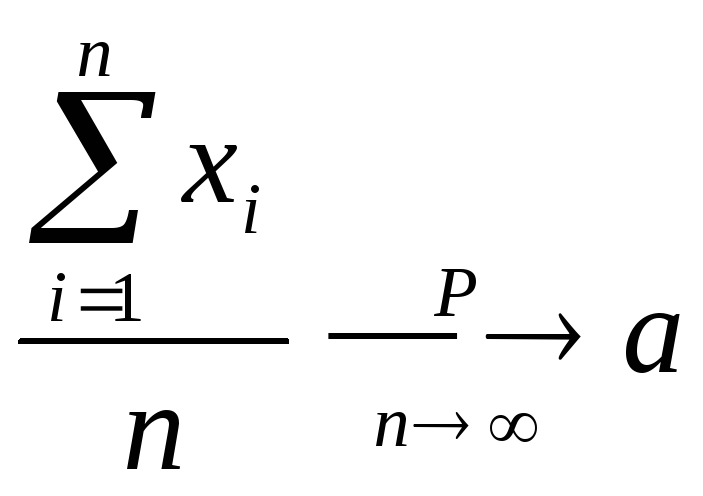
2. Теорема Чебишева і її наслідок застосовуються на практиці. Наприклад, страховій компанії необхідно встановити розмір страхового внеску, який повинен сплачувати страхувальник; при цьому страхова компанія зобов'язується сплатити при настанні страхового випадку визначену суму. Роздивляючись частоту (збитки страхувальника) при настанні страхового випадку як величину випадкову, визначається середнє число (середні збитки) при настанні страхових випадків, яке на основі теореми Чебишева з великим степенем впевненості можна вважати величиною не випадковою. На підставі цих даних і передбачуваної страхової суми визначається розмір страхового внеску.

Без урахування дії закону великих чисел можливі значні збитки страхової компанії або втрата привабливості страхових послуг.

Приклад:

Для визначення середньої тривалості горіння електроламп в партії з 200 однакових ящиків було взято на вибірку по одній лампі з кожного ящика. Оцінити імовірність того, що середня тривалість горіння відібраних 200 ламп відрізняється від середньої тривалості горіння ламп у всій партії не більш ніж на 5 годин (по модулю), якщо відомо, що середнє квадратичне відхилення тривалості горіння ламп в кожному ящику менше 7 годин.

Рішення:

Нехай Х_і – тривалість горіння електролампи взятої з і-го ящика. . Отже, середня тривалість горіння ламп у всій партії , тоді .

Приклад:

Скільки необхідно провести вимірювань даної величини, щоб з імовірністю, не менш ніж 0.95 гарантувати відхилення середньої арифметичної цих вимірювань від вірного значення величини не більш ніж на 1 (по модулю), якщо середнє квадратичне відхилення кожного вимірювання ≤5?

Рішення:

Х_і – результат і-го вимірювання,

За формулою і .