dinamics time series / 5

Здесь из полосы ± 2/√T = ± 0.089 выходят только значения выборочной PACF, соответствующие лагам k = 1, 2. В соответствии с приближенным критерием, упомянутым ранее, это приводит к неотвержению гипотезы H0: Xt ~ AR(2).

Для подтверждения этой гипотезы сравним значения информационных критериев Акаике и Шварца, получаемые при оценивании AR моделей 4-го, 3-го, 2-го и 1-го порядков, допускающих ненулевое математическое ожидание соответствующих AR процессов.

Оба критерия выбирают модель AR(2).

Если мы не ограничиваем себя моделями AR и допускаем, что модель, порождающая данные, имеет вид ARMA(p0, q0) (с неизвестными p0, q0)

a(L) Xt = b(L) εt ,

то в этом случае имеется несколько процедур оценивания пары (p0, q0), одну из которых мы сейчас рассмотрим (см. [Kavalieris (1991)]).

На первом шаге этой процедуры уже известными нам методами производится подбор модели авторегрессии AR(k)

∑k ak j Xt − j =εt , ak 0 =1, j = 0

вычисляются оценки коэффициентов aˆk j , j = 1, … , k, и на их основе получаются оценки инноваций

Порядок k авторегрессионной модели на этом шаге должен быть достаточно высоким. Его можно выбрать, опираясь на сравнение значений критерия Акаике для оцененных моделей авторегрессии различных порядков. (Вспомним, что критерий Акаике склонен завышать порядок модели, а это в данном случае нас как раз и устраивает.)

На втором шаге берутся регрессии Xt на Xt – j , j = 1, …, p, и регрессии Xt на εˆk (t – j), j = 1, …, q. По первым из них получаем начальные оценки наименьших квадратов

www.iet.ru/mipt/2/text/curs_econometrics.htm

на основании которой строим уточненную оценку для дисперсии инноваций

~1 ∑T ~

σp2, q = T t =1εt2 .

При этом предполагается, что сами инновации, зная точно коэффициенты ARMA

≥ q0 , что ведет к состоятельности оценок (~p, q~).

3.2. Оценивание коэффициентов модели

После того как произведена идентификация (стационарной) модели ARMA, т.е. на основании имеющихся наблюдений принято решение о значениях p, q в модели ARMA(p, q), порождающей данные, переходят к этапу оценивания коэффициентов модели. На этом этапе обычно используется метод максимального правдоподобия, который в конечном счете сводится к методу наименьших квадратов. За исключением некоторых наиболее простых случаев (например, модели AR(1)), эта задача решается итерационными методами, требующими задания некоторых “начальных” (“стартовых”) значений параметров, которые затем последовательно уточняются.

В качестве таких начальных значений можно использовать предварительные оценки, полученные на первом этапе. Такие начальные значения можно найти, приравнивая неизвестные “истинные” значения автокорреляций ρ(k) значениям r(k) выборочной автокорреляционной функции и используя функциональную связь между значениями ρ(k) и значениями коэффициентов модели. Например, если оценивается модель AR(p), то коэффициенты a1, …, ap определяются из системы первых p уравнений Юла – Уокера

www.iet.ru/mipt/2/text/curs_econometrics.htm

в которые вместо неизвестных значений ρ(1), …, ρ(p) автокорреляций подставляются наблюдаемые (вычисляемые по реализации ряда) значения r(1), …, r(p) выборочных автокорреляций.

При оценивании моделей с MA(q) составляющей (q > 0) существенным оказывается условие обратимости, сформулированное в разд. 2.5. Покажем это на примере MA(1) модели

Xt – µ = εt + bεt–1 , t = 1, … , T .

Имея наблюдаемые значения x1, x2, … , xT , мы последовательно выражаем ε1, ε2, … , εT через эти значения и (ненаблюдаемое) значение ε0 :

ε1 = X1 – µ – bε0 ,

ε2 = X2 – µ – bε1 = X2 – µ – b(X1 – µ – bε0) = (X2 – µ) – b(X1 – µ) + b2 ε0,

…

εT = XT – µ – bεT – 1 = (XT – µ) – b(XT – 1– µ) + b2(XT – 2– µ) –

+(–1)T – 1 b T – 1 (X1 – µ) + (–1)T b T ε0 .

Максимизация (по b) условной функции правдоподобия, соответствующей наблюдаемым значениям x1, x2, … , xT при фиксированном значении ε0 , равносильна минимизации суммы квадратов

Q(b) = ε12 + ε22 + … + εT2 ,

которая является нелинейной функцией от b . Для поиска минимума этой суммы квадратов приходится использовать численные итерационные методы оптимизации, которые, в свою очередь, требуют задания начального (“стартового”) значения параметра b . Как мы уже говорили, такое стартовое значение может быть получено на этапе идентификации модели. Однако полученное в итоге итераций “оптимальное” значение b зависит от неизвестного нам значения ε0 , что затрудняет интерпретацию результатов. Задача интерпретации облегчается, если выполнено условие обратимости ‌ b ‌< 1, и при этом значение ‌b ‌существенно меньше 1.

Действительно, при выполнении этого условия можно просто положить ε0 = 0 . Эффект от такой замены истинного значения ε0 на нулевое быстро убывает, так что сумма квадратов, получаемая в предположении ε0 = 0, может служить хорошей аппроксимацией для суммы, получаемой при истинном значении ε0 , при достаточно большом количестве наблюдений. Те же аргументы пригодны и для модели MA(q) с q > 1 : в этом случае можно положить ε0 = ε–1 = … = ε − q +1 = 0 . Для получения более

точной аппроксимации, в пакетах статистических программ (в том числе и в EVIEWS) предусмотрена процедура (backcasting) , в которой процесс итераций включает в себя также и оценивание значений ε0 , ε–1 , … , ε − q +1 путем построения для них “обратного

прогноза”.

Если в результате оценивания получена модель, в которой условие обратимости не выполняется, рекомендуется повторить процедуру оценивания с использованием другого набора начальных значений.

Более подробное изложение процедур оценивания стационарных ARMA моделей методом максимального правдоподобия можно найти, например, в книге [Hamilton (1994)]. Там же можно прочитать о том, каким образом вычисляются приближения для стандартных ошибок оценок коэффициентов этих моделей, которые можно использовать при большом количестве наблюдений обычным образом.

В заключение необходимо только сделать одно важное замечание. Пусть мы имеем стационарную AR(p) модель

a(L) Xt = δ + εt .

www.iet.ru/mipt/2/text/curs_econometrics.htm

Мы уже говорили о том, что в этом случае математическое ожидание µ процесса Xt связано с константой δ соотношением

При этом можно сначала оценить коэффициенты a1, … , ap и δ , применяя обычный метод наименьших квадратов к модели

Xt = δ + a1 Xt–1 + a2 Xt–2 + … + ap Xt–p + εt ,

а затем, используя полученные оценки aˆ1, ..., aˆ p и δˆ , получить оценку для µ в

виде

Однако можно поступить и иначе, как это предусмотрено, например, в пакете EVIEWS (Econometric Views), используемом нами в последующих примерах. Именно, мы можем записать ту же модель в виде

Xt = µ (1 – a1 – a2 – …– ap) + a1 Xt–1 + a2 Xt–2 + … + ap Xt–p + εt

и одновременно оценивать и a1, … , ap и µ . Такая процедура теоретически более эффективна. Однако в такой форме модель оказывается нелинейной по параметрам, и это обстоятельство, как и при оценивании MA моделей, требует применения нелинейного метода наименьших квадратов (NLLS – nonlinear least squares) и численных итерационных методов оптимизации.

Пример

Рассмотрим данные о годовом потреблении рыбных продуктов в США (на душу населения, в фунтах).

www.iet.ru/mipt/2/text/curs_econometrics.htm

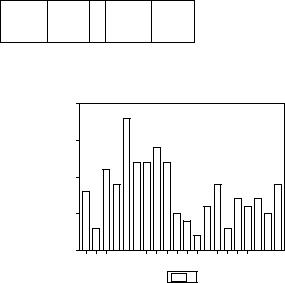
Коррелограмма, построенная по этим данным, имеет вид

Ориентируясь на указанные ранее приближенные критерии, прежде всего найдем значение 2/√T = 2/√20 = 0.447. Из полосы ± 0.447 не выходит ни одна из выборочных автокорреляций и частных автокорреляций. Поэтому с точки зрения этих критериев, мы не должны отвергать гипотезу о том, что наблюдаемый ряд порождается моделью

MA(0)

X0 = µ + εt .

С другой стороны, если ориентироваться на критерий Люнга – Бокса, то пик ACF на лаге 1 является статистически значимым. Это означает, что в качестве потенциальных моделей порождения данных можно предварительно рассматривать модели AR(1) и MA(1). Таким образом, мы сталкиваемся здесь с конфликтной ситуацией: статистические выводы, получаемые при использовании разных критериев, не соответствуют друг другу. Подобная ситуация не является чем-то исключительным и достаточно часто встречается при идентификации модели, порождающей наблюдаемый ряд, тем более, что используемые критерии – асимптотические, тогда как обычно в распоряжении исследователя имеется не слишком большое количество наблюдений.

www.iet.ru/mipt/2/text/curs_econometrics.htm

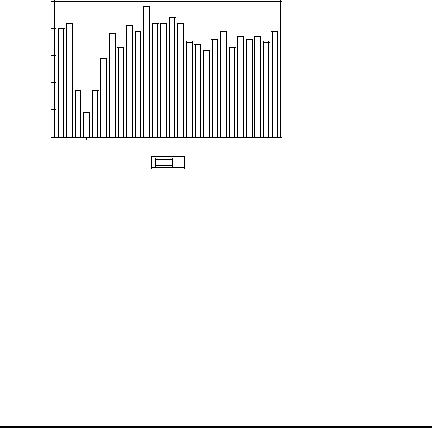
Последнее обстоятельство связано в значительной степени с тем, что для многих экономических рядов периоды, на которых порождающая ряд модель может считаться стационарной, обычно непродолжительны из-за изменения общей экономической обстановки, в которой эволюционирует рассматриваемый ряд. Это соображение можно легко проиллюстрировать на примере того же самого ряда данных о потреблении рыбных продуктов в США, если привлечь дополнительно статистические данные за период с 1940 по 1945 годы (годы Второй мировой войны). Эволюция ряда на расширенном периоде с 1940 по 1965 годы представлена следующим графиком:

Провал траектории ряда в 1942 – 1944 г.г. не позволяет трактовать этот ряд как стационарный на всем периоде с 1940 по 1965 годы. Поэтому мы продолжаем далее рассматривать значения ряда только на послевоенном периоде – с 1946 по 1965 г.г.

Если остановиться на модели AR(1), то для нее, как мы знаем, ρ(1) = a1. Поэтому приравнивая неизвестное значение ρ(1) значению r(1) = 0.429, мы получаем предварительную оценку для неизвестного значения a1. В то же время, производя непосредственное оценивание модели AR(1) с ненулевым математическим ожиданием нелинейным методом наименьших квадратов, получаем следующие результаты.

Dependent Variable: X

Method: Least Squares Sample(adjusted): 1947 1965

Included observations: 19 after adjusting endpoints Convergence achieved after 3 iterations

В данной ситуации уточненная оценка практически совпадает с предварительной

уравнению b1/(1 + b12) = 0.429. Корни последнего уравнения равны 0.567 и 1.704.

www.iet.ru/mipt/2/text/curs_econometrics.htm

3.3. Диагностика оцененной модели

После выбора типа и оценивания коэффициентов модели производится диагностика оцененной модели, т.е. выяснение того, насколько хорошо модель соответствует данным наблюдений (адекватна данным наблюдений) – это является третьим этапом процедуры подбора модели.

Для целей диагностики можно использовать целый ряд различных статистических процедур, которые направлены в основном на проверку гипотезы H0 о том, что в модели, порождающей наблюдения, последовательность εt действительно образует процесс белого шума.

Пусть мы остановили свой выбор на этапе идентификации на модели ARMA(p, q) a(L) Xt = b(L) εt ,

т.е.

Xt = a1 Xt–1 + … + ap Xt–p + εt + b1 εt–1 + … + bq εt–q ,

и на втором этапе оценили ее как

ˆ

b(L) , соответственно:

εˆt = aˆˆ(L) Xt . b(L)

На практике, конечно, мы можем использовать эту формулу лишь частично, поскольку бесконечный ряд в правой части приходится обрывать из-за наличия только конечного количества наблюдений.

При большом количестве наблюдений поведение εˆt должно имитировать поведение

самих εt . Cледовательно, если ошибки εt образуют процесс белого шума, то остатки должны имитировать процесс белого шума.

www.iet.ru/mipt/2/text/curs_econometrics.htm

Основываясь на этом соображении, Бартлетт [Bartlett (1946)] и Бокс и Пирс [Box, Pierce (1970)] предложили исследовать статистическую значимость выборочных автокорреляций для ряда инноваций εt

T∑− kεˆtεˆt + k

rε (k) = t =1T

∑εˆt2

t=1

исуммы их квадратов

M

QBP = T ∑rε2 (k) (Q-статистика Бокса – Пирса).

k =1

Если модель правильно специфицирована, то QBP имеет распределение, которое близко к распределению χ2(M – p – q), при условии, что T и M велики, а отношение (M/T) мало. Гипотеза адекватности подобранной модели отвергается, если

Люнг и Бокс предложили два способа преодоления проблемы смещения. Первый – прямой метод – состоит в использовании приближения

QBP ≈ χ2(E(QBP)) ,

где для E(QBP) используется указанное выше выражение (модифицированный критерий Бокса – Кокса).

Второй способ учитывает более точное выражение для D(rε(k)) – вместо (1/T)

берется (T – k)/(T2 + 2T). Это приводит к Q-статистике Люнга – Бокса

чем распределение статистики QBP . При этом качество приближения ухудшается, если значения параметров находятся вблизи границы стационарности или обратимости модели; особенно это заметно при малых M . Заметим, что хотя первоначально вывод асимптотического распределения статистики Люнга – Бокса производился в предположении, что εt – гауссовский белый шум, в дальнейшем было установлено, что этот критерий достаточно устойчив к отклонениям распределения εt от нормального. Важно только, чтобы была конечной дисперсия D(εt). ( Последнее условие часто нарушается для рядов, описывающих эволюцию быстро изменяющихся финансовых показателей – цен на акции, биржевых индексов, обменных курсов. Для таких рядов

www.iet.ru/mipt/2/text/curs_econometrics.htm

В пакете EVIEWS в распечатке результатов оценивания моделей ARMA рядом с коррелограммой ряда остатков приводятся P-значения для наблюдаемых значений Q– статистики Люнга – Бокса.

Для только что рассмотренных моделей AR(1) и МA(1) коррелограммы рядов остатков имеют следующий вид.

Для модели AR(1):

www.iet.ru/mipt/2/text/curs_econometrics.htm