dinamics time series / ГЛ5

А для ряда NONDURABLE

Если отвлечься от видимой нестационарности этих рядов, то поведение выборочных ACF и PACF предполагает идентификацию обоих рядов как рядов типа AR(1). Имея в виду наличие у рядов выраженного линейного тренда, произведем оценивание моделей

Xt = α + β t + a1Xt –1 + ut .

(Здесь мы используем обозначение ut , а не εt , поскольку ряд ut на этот раз может и не являться белым шумом.)

www.iet.ru/mipt/2/text/curs_econometrics.htm

Это приводит к следующим результатам.1 Для ряда GNP:

Dependent Variable: GNP Method: Least Squares Sample(adjusted): 1947:2 1961:4

Included observations: 59 after adjusting endpoints Convergence achieved after 3 iterations

Остатки обнаруживают явную автокоррелированность : P-значение критерия Бройша – Годфри при альтернативе AR(1) равно 0.0000. Переоценивание с включением в модель запаздывания на два квартала, дает:

Dependent Variable: GNP Method: Least Squares Sample(adjusted): 1947:3 1961:4

Included observations: 58 after adjusting endpoints Convergence achieved after 3 iterations

Модули комплексных чисел, обратных авторегрессионным корням, равны 0.7926, что говорит в пользу стационарности детрендированного ряда

Xt0 = Xt – µ – γ t .

K построению модели для ряда GNP можно подойти и иначе. Сначала произвести детрендирование ряда, оценивая модель

Xt = µ + γ t + ut :

1 Приводимые в таблицах оценки константы (C) и коэффициента при переменной t (T) соответствуют оценкам µ и γ в представлении

(Xt – µ – γt ) = a1(Xt – 1 – µ – γ( t – 1)) + a2(Xt – 2 – µ – γ( t – 2)) + ut

(a2 = 0 для первой из двух таблиц). Эти оценки получаются применением нелинейного метода наименьших квадратов. При этом обозначение AR(1) указывает на оценку для a1 , а AR(2) – на оценку для a2 .

www.iet.ru/mipt/2/text/curs_econometrics.htm

Остатки, полученные при оценивании этой модели, образуют оцененный детрендированный ряд, коррелограмма которого

позволяет идентифицировать этот ряд как AR(2). После этого можно строить AR(2) модель для (оцененного) детрендированного ряда

Объединяя результаты последних двух оцениваний, получаем оцененную модель

Xt – 218.4825 – 5.181995 t =

=1.379966 (Xt–1 – 218.4825 – 5.181995(t–1)) –

–0.630426 (Xt–2 – 218.4825 – 5.181995(t–2)),

или

Xt = [(1– 1.379966 + 0.630426)·218.4825

+1.379966·5.181995 – 0.630426·5.181995·2]

+(1 – 1.379966 +0.630426) ·5.181995 t

+1.379966 Xt–1 – 0.630426 Xt–2 + et

=55.338375 +1.297882 t + 1.379966 Xt–1 – 0.630426 Xt–2 + et .

Вто же время, по приведенным результатам оценивания модели

Xt = α + β t + a1Xt–1 + a2Xt–2 + ut

получаем

Xt – 217.7399 – 5.221538 t =

=1.380274 (Xt–1 – 217.7399 – 5.221538(t–1))

–0.630066 (Xt–2 – 217.7399 – 5.221538(t–2)),

или

Xt = [(1– 1.380274 + 0.630066)·217.7399

+1.380274·5.221538 – 0.630066·5.221538·2]

+(1 – 1.380274 +0.630066) ·5.221538 t

+1.380274 Xt –1 – 0.630066 Xt –2 + et

=55.017011 + 1.304298 t + 1.380274 Xt–1 – 0.630066 Xt–2 + et ,

www.iet.ru/mipt/2/text/curs_econometrics.htm

так что результаты, полученные при использовании обоих вариантов построения модели, практически совпадают. Поэтому можно использовать смешанный вариант – использовать детрендированный ряд для идентификации порядка модели, а оценивать идентифицированную модель вместе с включенным в нее трендом, в данном случае – оценивать модель Xt = α + β t + a1Xt–1 + a2Xt–2 + ut .

Заметим, что диагностика рядов остатков в обеих оцененных моделях говорит в пользу их адекватности.

Перейдем теперь к ряду NONDURABLE. Коррелограмма детрендированного ряда (ряда остатков от оцененной модели регрессии Xt на константу и t )

обнаруживает резко выделяющийся пик на лаге 1, так что можно попробовать оценить модель Xt = α + β t + a1Xt–1 + ut . Это дает следующие результаты:

Наблюдаемые P-значения статистик Люнга – Бокса для ряда остатков превышают 0.05 при всех выборах M от 1 до 20. Проверка на отсутствие автокоррелированности по критерию Бройша – Годфри дает P-значения, большие 0.05, как при AR(1) альтернативе, так и при альтернативах AR(2), AR(3) и т.д. Наконец, при проверке нормальности P-значение статистики Jarque – Bera равно 0.648 , так что по совокупности этих результатов мы могли бы говорить о пригодности оцененной модели

Xt – 47962.75 – 315.1909 t =

= 0.884803 (Xt–1 – 47962.75 – 315.1909 (t–1)) + et .

Обратим, однако, внимание на следующее обстоятельство. Оцененное значение 0.884803 коэффициента при Xt–1 достаточно близко к единице, и если ориентироваться на вычисленное значение 0.080824 стандартной ошибки для этого коэффициента, то при допущении отклонений от оцененного значения в пределах двух стандартных ошибок, в интервал допустимых значений 0.884803 ± 2·0.080824 попадают и значения, большие или равные 1. Но последние соответствуют нестационарному процессу авторегрессии.

Таким образом, несмотря на то, что при полученной точечной оценке 0.884803 коэффициента при Xt–1 построенная модель формально оказывается стационарной относительно детерминированного линейного тренда (т.е. детрендированный процесс следует стационарной AR(1) модели), мы не можем с достаточной степенью

www.iet.ru/mipt/2/text/curs_econometrics.htm

уверенности гарантировать, что истинная модель порождения наблюдений также стационарна относительно линейного тренда.

Между тем вопрос о стационарности или нестационарности модели, порождающей наблюдаемый ряд, привлекает к себе постоянное внимание уже в течение нескольких десятков лет. Особенно это внимание усилилось после серии работ 80-х годов 20 века, в которых было введено понятие коинтеграции. С помощью этого понятия была обоснована методика построения “моделей коррекции ошибок”, в рамках которых удается моделировать наличие долговременных связей между переменными вместе с указанием краткосрочной динамики, обеспечивающей поддержание этих долговременных связей.

В последующем изложении мы рассмотрим вопросы, связанные с методами различения стационарных (стационарных относительно детерминированного тренда) и нестационарных рядов в рамках ARMA моделей, а также вопросы построения моделей связи между временными рядами.

5.1. Нестационарные ARMA модели

Начнем рассмотрение с наиболее простой модели – процесса AR(1)

Xt = a1Xt–1 + εt .

Мы уже знаем, что такой процесс является стационарным при выполнении условия – 1< a1 < 1. А как проявляется нестационарность ряда Xt при нарушении этого условия? Приведем смоделированные реализации такого ряда при a1 = 0.5, a1 = 0.7, a1 = 0.9, a1 = 1, a1 = 1.05, a1 = 1.1.

www.iet.ru/mipt/2/text/curs_econometrics.htm

имитирующая гауссовский белый шум с дисперсией, равной единице:

NOISE

Однако поведение смоделированных рядов оказалось качественно различным. Полезно проследить, как изменяется характер траектории ряда c возрастанием значений коэффициента a1 от a1 = 0.5 до a1 = 1.1. Заметим при этом, что в порождающих моделях математические ожидания Xt равны нулю.

www.iet.ru/mipt/2/text/curs_econometrics.htm

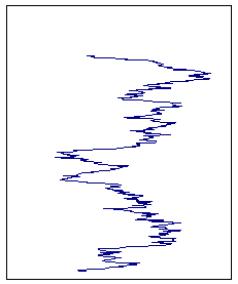
При возрастании значения a1 от a1= 0 (белый шум) до a1= 1 количество пересечений нулевого уровня уменьшается, все более длинными становятся периоды, в течение которых значения ряда находятся по одну сторону от нулевого уровня. Расширенный график ряда при a1= 1, продленный до 500 наблюдений, иллюстрирует характерное свойство реализаций процесса

Xt = Xt–1 + εt ,

состоящее в том, что такой процесс, начавшись в момент t = 1 со значения Xt = x1 (в данном случае x1 = 0), в дальнейшем очень редко пересекает уровень x1 (“возвращается к уровню x1 ”) и, находясь в течение длительного времени по одну сторону от этого уровня (выше или ниже), может удаляться от этого уровня на значительные расстояния.

www.iet.ru/mipt/2/text/curs_econometrics.htm

“Повернутая вертикально”, траектория ряда напоминает траекторию движения сильно нетрезвого человека, пытающегося продвигаться вперед по прямой, но не имеющего возможности успешно выдерживать нужное направление. И это служит некоторым оправданием термина, используемого для AR(1) процесса с a1= 1:

Xt = Xt –1 + εt – случайное блуждание (процесс случайного блуждания – random walk).

Далее мы рассмотрим этот процесс подробнее, а сейчас обратим внимание на поведение реализаций процесса

Xt = a1Xt–1 + εt

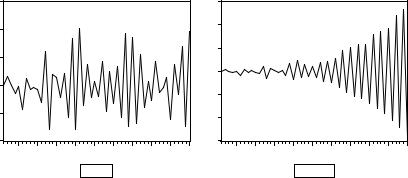
при a1 = 1.05 и a1 = 1.1. Обе реализации иллюстрируют “взрывной” (“explosive”) характер поведения AR(1) процесса при a1 > 0: траектории процесса очень быстро удаляются от начального уровня на все возрастающие расстояния. В связи с этим “взрывные” модели непригодны для описания поведения макроэкономических рядов на сколь-нибудь протяженных интервалах времени.

Пониманию столь различного поведения реализаций AR(1) процесса помогает представление модели в виде

Xt – Xt–1 = a1Xt–1 – Xt–1 + εt = (a1 – 1)Xt–1 + εt ,

или

∆Xt = φ Xt–1 + εt ,

где

∆Xt = Xt – Xt–1 , φ = a1 – 1.

При a1 = 1 имеем φ = a1 – 1= 0, и приращения ∆ Xt ряда Xt образуют процесс белого шума, так что условное математическое ожидание ∆ Xt при фиксированном (наблюдаемом) значении Xt–1 = xt–1 не зависит от xt–1 и равно 0. Соответственно, при фиксированном (наблюдаемом) значении Xt–1 = xt–1 , условное математическое ожидание случайной величины Xt = ∆Xt + Xt–1 равно xt–1 . Если распределение случайной величины εt симметрично относительно нуля (а именно таково и гауссовское распределение, которое использовалось нами при моделировании), то

www.iet.ru/mipt/2/text/curs_econometrics.htm

наблюдаемое значение Xt = xt может с равным успехом оказаться как больше, так и меньше xt–1 . Именно это и определяет “блуждающий” характер траектории ряда.

При a1 > 1 имеем φ = a1 – 1 > 0, и условное математическое ожидание ∆ Xt при фиксированном (наблюдаемом) значении Xt–1 = xt–1 , равное E(∆ Xt│Xt–1 = xt–1) = φ

удалению траектории процесса от начального уровня, что и наблюдалось нами для реализаций AR(1) модели при a1 = 1.05 и a1 = 1.1.

Наконец, при 0 < a1 < 1 имеем φ = a1 – 1 < 0, и условное математическое ожидание ∆ Xt при фиксированном (наблюдаемом) значении Xt–1 = xt–1 , равное E(∆ Xt│Xt–1 = xt–1) = φ xt–1 , имеет знак, противоположный знаку xt–1. Таким образом, если xt–1 > 0, то ожидаемое значение следующего наблюдения Xt = xt меньше значения xt–1 , а если xt–1 < 0, то ожидаемое значение следующего наблюдения Xt = xt больше значения xt–1 . Наличие такого механизма обеспечивает удержание траектории процесса в относительной близости от уровня, равного безусловному математическому ожиданию E(Xt) = µ ряда (в данном случае, µ = 0), и достаточно частое пересечение траекторией ряда этого уровня.

Мы ограничились здесь рассмотрением ситуаций с a1 > 0, поскольку они наиболее типичны для экономических временных рядов. Для полноты приведем также и смоделированные реализации процесса Xt = a1Xt–1 + εt при a1 = – 1 и a1 = –

1.1.

Обратимся теперь к процессу случайного блуждания

Xt = Xt–1 + εt , t = 1, …, T ,

со стартовым значением X0 = x0 . Мы можем представить Xt в виде

Xt = Xt–1 + εt = (Xt–2 + εt–1) + εt = Xt–2 + εt–1 + εt = (Xt–3 + εt–2) + εt–1 + εt =

Отсюда сразу получаем:

www.iet.ru/mipt/2/text/curs_econometrics.htm