Файловый архив студентов. Файловый архив студентов.
1308 вузов, 5224 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Донецкий национальный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Krivolinejnie_i_poverhnostnie_integrali

.pdf
Скачиваний:
54
Добавлен:
13.04.2015
Размер:
645.02 Кб
Скачать
☆

Окончательно получим

x2dydz y2dxdz z2dxdy I1 .

S

Пример 8. s y z dydz z x dxdz x y dxdy I

S - верхняя сторона поверхности, вырезанной цилиндром x2 y2 2ax из сферы: x2 y2 z2 2Rx, R 0, z 0.

Решение. Зададим поверхность параметрически. Так как z 0 , то S:

z 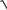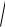2R x x2 y2x x

y y

x, y D Sxoy : x a 2 y2 a2

Нормаль к внешней стороне поверхности сферы образует с осью OZ

острый угол, т.е. cos 0 , следовательно, берём знак "+".

 

 

2Rx x

2

y

2

A

2Rx x

2

y

2

x B x y C

 

I y

 

 

 

 

dxdy ,

D

 

 

 

 

 

 

 

 

 

 

 

 

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R x

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

x

 

 

 

 

 

 

 

 

2Rx x

2

y

2

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

x

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

x

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

2Rx x2 y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2Rx x2 y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

R x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

z

 

 

 

2Rx

x

2

y

2

 

 

 

 

 

 

R x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

x

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

z

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2Rx x2 y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2Rx x2 y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

C

 

x

 

 

x

 

x

 

 

y

 

 

y

 

 

y

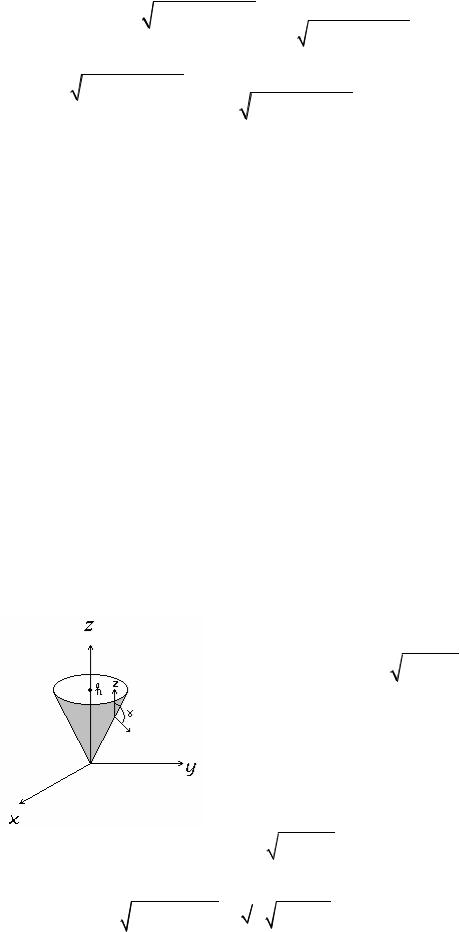
10

1

01

т.о.

 

 

 

 

 

 

R x

 

 

 

 

 

 

2

 

2

 

 

 

I y

2Rx x

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

2Rx x

 

y

 

 

 

 

D

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

2Rx x2 y2

x

 

 

 

 

 

x y dxdy

 

 

 

 

 

 

 

2

 

2

 

 

 

2Rx x

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x R

 

y

 

 

y R

 

 

R x

 

x y dxdy

R

 

R

D

 

 

 

 

 

 

 

 

 

y

 

 

R

 

 

1

 

dxdy Ra2.

R

 

 

 

 

x a 2 y2 a2

 

 

 

 

 

Здесь

 

dxdy равен площади круга радиуса a .

x a 2 y2 a2

 

 

 

 

 

 

ydxdy 0,

x a 2 y2 a2

т.к. область D симметрична относительно оси ОХ, а подынтегральная функция, нечетная относительно y.

Пример 9. Вычислить

y z dydz z x dzdx x y dxdy ,

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S - внешняя сторона конической поверхности

x2 y2

z2 0 z h . (без

„крышки”).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение.

Зададим S параметрически:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

2

y

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

cos 0

 

 

 

 

 

 

D : x2 y2 h2

 

 

 

 

 

 

 

x x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найдём направляющие косинусы в случае,

 

 

если поверхность задана в явном виде. Т.к. 0 z ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

то из уравнения поверхности z

 

 

x2 y2

 

 

 

 

 

 

 

cos

 

dxdz

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 z1x2 z1y2

2

 

x2 y2

 

 

 

 

 

 

 

cos

 

 

y

 

 

 

 

;

 

 

 

 

 

 

 

2

 

x2 y2

cos 1 . 2

y z x z x y x y dS

s s

xy xz zy xy x y dS zy xz x y dS

s s

 

 

y x z x, y 1

1 z1x2 z1y

 

ПрSxoy

y x

 

1

 

 

 

 

 

 

dxdy

 

x2 y2

2

x2 y2 h2

2

h

 

 

 

 

 

d sin cos 1

 

d 0 .

2

0

0

 

 

 

 

 

Выкладки подробные можно проделать самостоятельно.

В упражнении №4 направляющие косинусы могут быть найдены из

общих формул при параметризации поверхности S:

 

 

 

 

 

 

 

x x

 

 

 

 

 

 

 

 

 

 

D : x2 y2 h2

y y

 

 

 

x, y

 

 

 

 

 

 

x2 y2

z z

 

 

 

 

 

 

 

 

Роль параметра u

играет x , параметра V - y .

Поэтому формула (2) примет вид

y2 z2 dxdy y2 z2 x,y C dxdy.

s

D

Так как нормаль к верхней стороне поверхности S образует острый угол с осью OZ , то очевидно, cos 0 . С другой стороны

cos

 

 

 

C

 

 

 

 

, где C

X x1

Yx1

 

 

1

0

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X

1y

Yy1

 

0

1

 

A

2

B

2

C

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C 0, поэтому перед радикалом, а значит и перед двойным интегралом

нужно взять знак "+".

Итак

 

 

 

2

 

a

b

2

 

 

 

 

 

 

I y2

a2 x2

 

dxdy dx y2 x2 a2 dy

ab b2 2a2

.

 

3

D

 

 

 

 

a

0

 

 

7. Элементы теории поля.

7.1. Основные теоретические сведения и образцы решения типовых задач по теме «Элементы теории поля».

7.1.1. Определение скалярного поля.

Пусть D - область в E3 (или в E2 ). Говорят, что в D задано скалярное поле, если M D поставлено в соответствие некоторое число u M .

Физические примеры скалярных полей: поле температуры какого-либо тела, поле плотности масс и тому подобное.

Если в пространстве введена прямоугольная система координат, то скалярное поле задается функцией u u x, y, z , x, y, z D .

7.1.2.Характеристики скалярного поля.

1)Поверхность (линия), на которой функция u M принимает

постоянные значения, называется поверхностью (линией) уровня: u M C .

2)Производная по направлению.

Пусть

u M

- скалярное

поле, заданное

в области D ,

e -

единичный вектор,

 

 

 

 

 

 

 

 

 

e cos ,cos ,cos

 

(1)

 

 

 

 

 

 

Пусть

M - любая точка из

D , отличная от

M , такая, что вектор

MM коллинеарен

e . MM

- величина направленного отрезка

MM

( MM

 

MM

 

, если векторы

MM и e сонаправлены и MM

 

MM

 

,

 

 

 

 

если эти векторы противоположно направлены).

 

 

 

 

 

 

Определение.

 

Число

 

lim

u M u M

 

 

 

u

M

называется

 

 

 

MM

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M M

 

 

 

 

 

e

 

производной скалярного

поля u M в точке

M по направлению

вектора e .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если скалярное поле u u x, y, z

дифференцируемо в точке M , то

 

u

 

u

cos

u

cos

u

cos

 

(2)

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

x

 

y

 

 

z

 

 

 

 

 

 

 

 

 

Производная

u

M

 

является

скоростью

 

 

изменения

скалярного

 

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

поля u x, y, z в точке M в направлении вектора e .

3)Градиент скалярного поля.

Определение. Градиентом скалярного поля u x, y, z называется

вектор-функция

 

 

 

u

 

 

 

 

 

 

 

u

 

u

(3)

 

 

 

 

 

grad u

 

 

i

 

j

 

k

 

 

 

 

x

 

z

 

 

 

 

 

 

 

 

 

 

y

(1),

(2)

 

(3),

 

 

Учитывая

равенства

и

легко видеть

что

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M grad u M ,e . Откуда следует, что

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M

grad u M

cos ,

где

 

-

угол между векторами

e и

 

 

e

 

 

 

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

grad u M .

Очевидно, что

 

M

принимает

наибольшее значение,

если 0 .

 

 

 

 

 

 

 

e

 

 

 

 

 

 

grad u M

 

 

 

 

 

 

 

 

 

 

То есть

указывает направление наибольшей скорости

изменения поля в этой точке, а grad u M есть максимальная скорость

изменеия функции в точке M .

7.2. Векторные поля и их характеристики.

7.2.1. Определение векторного поля.

Говорят, что в области D (пространственной или плоской) задано векторное поле, если M D поставлен в соответствие некоторый вектор

A M .

Физические примеры векторных полей: поле скоростей потока жидкости, описываемое в каждой точке вектором скорости v M , магнитное

поле, создаваемое электрическим током и задаваемое в каждой точке вектором магнитной индукции b M и тому подобное.

7.2.2.Характеристики векторного поля.

1)Удобной геометрической характеристикой векторного поля A M

служат векторные линии – кривые, в каждой точке M которых вектор A M направлен по касательной к кривой.

 

Если

векторное

поле

 

A x, y, z P i Q j R k ,

то

векторные

 

линии этого поля описываются системой

 

 

 

 

 

 

 

 

 

dx

 

 

dy

 

 

dz

 

 

 

 

 

 

 

 

 

 

 

 

 

(4),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Конкретная

векторная

линия,

проходящая

через заданную

точку

 

M0 x0 , y0 , z0 ,

 

 

должна

 

удовлетворять

дополнительному

условию

 

 

x t0 x0 , y t0 y0 , z t0 z0 .

 

 

 

 

 

 

 

 

 

 

 

2)

Дивергенция.

 

 

 

Дивергенцией

 

 

 

 

 

 

 

 

 

Определение.

 

 

 

 

 

векторного

 

поля

 

 

A P x, y, z i Q x, y, z j R x, y, z k

называется

скалярная

 

функция

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

Q

R

 

 

 

 

 

 

(5).

 

 

 

 

 

 

 

 

 

 

 

 

 

divA

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dz

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

dy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Слово «дивергенция» означает «расходимость». Дивергенция

 

характеризует

 

 

плотность

источников

тока

векторного поля

в

 

рассматриваемой точке.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

Ротор.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Определение.

Ротором

 

(или

вихрем)

векторного

поля

 

 

A P i Q j R k называется векторная функция

 

 

 

 

 

 

 

dydz

 

 

dzdx

dxdy

 

 

R

 

Q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rotA

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

y

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

Q

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

R

 

 

 

 

Q

 

 

P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j

 

 

 

 

 

 

 

k

 

 

 

 

(6).

 

 

 

 

 

 

 

z

 

x

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ротор характеризует завихренность поля A в точке M .

 

 

 

4)

Поток векторного поля.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрим

векторное

поле

A P i Q j R k ,

определенное

в

 

области

 

 

 

 

D

 

 

 

и

некоторую

кусочно-гладкую

ориентированную

поверхность

S D .

Пусть

n M cos M i cos M j cos M k

- поле единичных

нормалей на выбранной стороне поверхности. Поверхностный второго рода интеграл

P cos Q cos R cos dS A,n dS

(7)

S

S

A M через

 

Называется

потоком векторного поля

выбранную

сторону поверхности S .

 

 

 

Если A v

- скорость движущейся

жидкости,

то

v, n dS

S

представляет собой количество жидкости, протекающей через выбранную сторону поверхности S за единицу времени.

Поэтому и в случае произвольного векторного поля A M интеграл

(1) называется потоком векторного поля через сторону поверхности

S.

5)Циркуляция векторного поля.

Пусть

задано

векторное поле A M P,Q, R

в некоторой

пространственной области D и задана кусочно-гладкая кривая L , на

которой

задано

направление обхода (ориентация

кривой). Пусть

M i dx j dy k dz - единичный касательный вектор к кривой

L в точке M .

 

 

Криволинейный интеграл

 

 

 

 

ds

(8)

Pdx Qdy Rdz A

L

L

 

 

называется

циркуляцией

векторного

поля A вдоль кривой L в

заданном направлении.

 

 

Если взять другое направление обхода кривой (изменить ориентацию), то вектор изменит свое направление на противоположное, а значит, и циркуляция изменит знак.

Если A F - силовое поле, то A ds представляет собой работу

L

силового поля F вдоль кривой L в выбранном направлении.

7.3. Формула Остроградского-Гаусса.

Пусть в

области D

определено векторное

поле A P,Q, R ,

S -

замкнутая

кусочно-гладкая

поверхность,

ограничивающая

D ,

n M cos ,cos ,cos

-

единичный вектор

внешней нормали

к

поверхности S в точке M , функции P,Q, R - непрерывно-дифференцируемы в замкнутой области D . Тогда справедлива формула Остроградского-Гаусса

 

P

Q

R

 

 

 

 

 

 

 

dxdydz P cos Q cos R cos dS .

 

 

 

D

 

x

y

z

S

 

 

 

P

 

Q

 

R

 

 

 

 

 

 

 

 

Учитывая, что

 

 

divA, а P cos Q cos R cos dS

dx

dy

 

A,n dS -

 

 

 

dz

S

 

 

 

 

 

 

 

поток

векторного

поля

через

внешнюю

сторону

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

поверхности S , формулу Остроградского-Гаусса

можно

записать

в

векторной форме так:

 

 

 

 

 

 

 

 

 

 

 

 

divAdxdydz A, n dS

 

 

(9)

 

 

 

 

D

 

 

 

S

 

 

 

 

 

 

 

 

 

 

Поток непрерывно-дифференцируемого

поля

A

в сторону

внешней

нормали кусочно-гладкой поверхности

S равен

тройному

интегралу

по

области

D , ограниченной этой поверхностью от дивергенции векторного

поля A.

 

(9)

 

 

 

 

 

 

 

 

 

 

 

 

Из

формулы

можно получить

другое определение

дивергенции

A,n dS

векторного поля A: M D

div A M lim

S

 

, где V -

объем

 

 

 

V M

V

 

области D , который стягивается в точку M .

 

 

 

Таким образом, div A M

характеризует источники (или стоки)

поля –

это поток векторного поля, проходящий через точку M . Чтобы поток через S был отличен от нуля, внутри области D должны быть источники (или стоки) поля. Само векторное поле как бы расходится от источников. Отсюда и происходит название «расходимость» или «дивергенция».

7.4. Формула Стокса в векторной форме.

Пусть в области D задано непрерывно-дифференцируемое векторное поле A P,Q, R , L - замкнутый кусочно-гладкий контур, лежащий в D .

S

- произвольная гладкая

поверхность,

границей которой

является

контур

L (поверхность

S

натянута

на

L ),

причем,

S D ,

n M cos ,cos ,cos -

единичная нормаль

на

выбранной

стороне

поверхности S .

 

 

 

 

 

 

Тогда справедлива формула Стокса

Pdx Qdy Rdz

L

 

 

 

R

 

Q

cos

P

 

R

cos

 

Q

 

P

cos dS ,

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

z

 

 

 

 

z

x

 

 

 

 

x

y

 

 

S

 

 

 

 

 

 

 

 

 

 

ориентация контура L согласована с ориентацией поверхности S .

 

Первая часть формулы Стокса есть циркуляция векторного поля A вдоль

кривой

 

 

L ,

 

 

а

 

 

 

правая

 

 

 

 

-

 

 

равна

потоку

 

R

 

Q

 

 

P

 

R

Q

 

 

P

 

 

 

 

 

rotA

 

 

 

 

 

 

i

 

 

 

 

 

 

j

 

 

 

 

k через поверхность S .

 

 

z

 

z

 

 

 

 

 

 

y

 

 

 

 

 

x

x

 

 

y

 

 

 

 

 

 

 

Поэтому формулу Стокса можно записать в векторной форме

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(10)

 

 

 

 

 

 

 

A dl rotA,n dS

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

 

 

 

 

 

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Поток ротора непрерывно-дифференцируемого поля A через выбранную сторону гладкой поверхности S численно равен циркуляции поля A вдоль края поверхности, причем ориентация края поверхности согласована с выбранной стороной поверхности S .

7.5. Потенциальное поле.

 

 

 

 

 

 

 

 

Определение.

Непрерывно

дифференцируемое

векторное

поле A

называется потенциальным в области D , если его можно представить в

этой области как градиент некоторого скалярного поля u x, y, z ,

A grad u .

Функция

u x, y, z называется скалярным потенциалом

векторного

поля A.

 

 

 

 

u

 

 

u

 

Очевидно,

если

A P,Q, R

потенциально в D ,

то P

,

Q

,

 

 

 

x y

R u то есть выражение Pdx Qdy Rdz du .

z

Учитывая определение потенциального поля, теорему о независимости

криволинейного

интеграла

от

пути

интегрирования,

модно

переформулировать следующим образом:

A P,Q, R

 

 

Теорема. Пусть векторное поле

непрерывно

дифференцируемо в поверхностно односвязной области D , тогда следующие

утверждения эквивалентны:

 

 

 

 

 

1)

поле A потенциально в D ;

 

 

 

 

2)

в D

u x, y, z -

потенциальная

функция,

такая,

что

Pdx Qdy Rdz du ;

3)циркуляция поля A вдоль любого замкнутого кусочно-гладкого контура D равна нулю

A d Pdx Qdy Rdz 0 ;

4) для A D

и B D циркуляция поля A вдоль кривой AB не

зависит от

выбора кривой AB и равна разности значений

потенциала u в точках A и B :

A d u B u A ;

5) поле A является безвихревым, то есть

rot A rot grad u 0 ;

Замечания.

1.Утверждение 4 означает, что работа силового потенциального поля вдоль кривой AB не зависит от выбора кривой, а зависит

только от конечной и начальной точек B и A .

2.Из утверждений 1 и 5 следует, что условие rot A 0 является

необходимым и достаточным условием потенциальности поля A в поверхностно односвязной области.

7.6.Соленоидальное поле.

Определение. Непрерывно дифференцируемое векторное поле A

называется соленоидальным в области D , если поток этого поля через

любую замкнутую кусочно-гладкую замкнутую поверхность S D равен нулю: A n dS 0.

S

Определение. Область D называется объемно-односвязной, если S - замкнутой, кусочно-гладкой S D , часть пространства, ограниченного S , также лежит в D .

Спомощью формулы Остроградского-Гаусса доказывается необходимое

идостаточное условие соленоидальности поля.

Теорема. Для того, чтобы непрерывно-дифференцируемое векторное поле A было соленоидальным в объемно-односвязной области, необходимо

и достаточно, чтобы div A 0.

7.7. Контрольные вопросы и задания по теме «Элементы теории поля».

1. Дайте определение скалярного поля. Приведите примеры.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности