
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В.
ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
КУРСА «ВЫСШАЯ МАТЕМАТИКА»
Учебное пособие
ЧАСТЬ 1
Утверждено на заседании Ученого совета экономического факультета Донецкого национального университета протокол № 8 от 18.04.2008 г.
Донецк – 2008
ББК 22.1
УДК 516+517(076.1)
Практикум по решению задач курса «Высшая математика»: Учебное пособие. Часть 1/Сост. Н.В.Румянцев, М.И.Медведева, Ю.Н.Полшков, А.В.Пелашенко.
–Донецк: ДонНУ, 2008. – 102 с.
Впрактикуме приведены задания для самостоятельной и индивидуальной работы по всем основным темам курса «Высшая математика». Рассмотрены подробные решения типовых задач, а также необходимый теоретический материал. Практикум составлен в соответствии с программой курса “Математика для экономистов”, изучаемой студентами всех экономических специальностей. Пособие может быть использовано преподавателями при подготовке и проведении практических занятий, а также для самостоятельной работы студентов любой формы обучения.
Рецензенты: д.ф-м.н., проф. Горр Г.В., д.т.н., проф. Улитин Г.М.
Ответственный за выпуск: Румянцев Н.В., д.э.н., проф.
©Донецкий национальный университет, 2008
©Н.В.Румянцев, М.И.Медведева, Ю.Н.Полшков, А.В.Пелашенко
2
РАЗДЕЛ 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ТЕМА 1
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Векторы. Линейные операции над векторами. Скалярное произведение векторов
Вектором AB =| a | называется направленный отрезок. Точка A – начало вектора, точка B – конец вектора (рис. 1.1). Длина отрезка AB называется модулем (длиной) вектора AB : | a |=| АВ| .
В
а
A
Рис. 1.1
Если известны координаты точек А(xA , yA , zA ) и В(xB , yB , zB ) , то координаты вектора а= AB можно найти по формуле
AB |
= (xB − xA , yB − yA , zB − zA ) . |
(1.1) |
|
|
|
Разложение вектора |
|
|
по ортам |
|
|
|
, |
|
|
, |
|
|
|
|
|
|
записывается в виде |
||||||||||||||||||||
|
а |
i |
j |
k |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= xi |
+ y j + zk , где i, |
j, k |
– единичные взаимно перпендикулярные векторы |
|||||||||||||||||||||||||||||||||||
(орты), совпадающие по направлению с координатными осями Ox, Oy, Oz . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
B |
|||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a +b |
|
|
|
|
|
||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
O |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
C |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Рис. 1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.3 |
|||||||||||||||||||
Суммой векторов a + b + c называется вектор ОС (рис. 1.2), начало ко-
торого совпадает с началом вектора a , а конец – с концом вектора c . В частно-
3
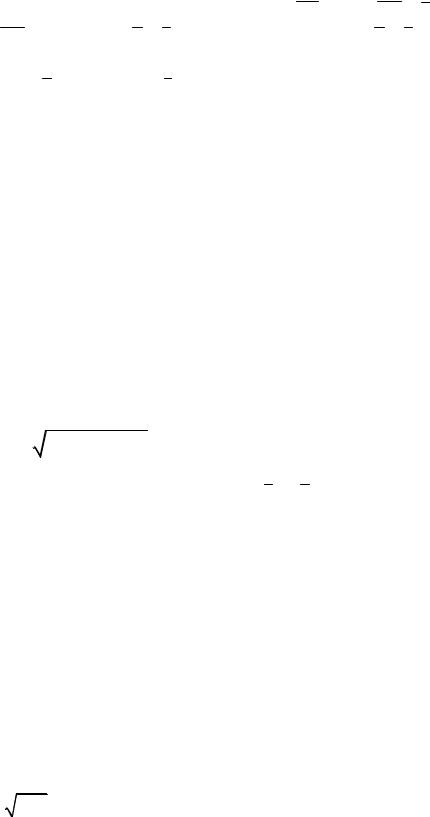
сти, в параллелограмме, построенном на векторах ОА=а и ОВ =b , одна век- тор-диагональ ОB есть сумма a + b , а другая есть разность a − b данных векторов (рис. 1.3).
Если векторы a = (x1, y1, z1 ) и b = (x2 , y2 , z2 ) заданы в координатной форме, то их сумма (разность) находится по формуле
|
a |
± |
|
|
b |
|
= (x1 ± x2 , y1 ± y2 , z1 ± z2 ) . |
(1.2) |
|||||||
Произведением вектора |
|
на число (скаляр) λ называется новый вектор, |
|||||||||||||
a |
|||||||||||||||
имеющий длину |
|
|
|
|
|
|
λ |
|
и одинаково направленный с вектором |
|
при λ > 0 или |
||||
|
a |
|
|
a |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположно направленный вектору |
a |
при λ < 0 . |
|||||||||||
В координатной форме произведение вектора |
|
на число λ определяется |
|||||||||||
a |
|||||||||||||
формулой |
|
|
|
||||||||||
λ |
|
|
|
|
= (λx1,λy1,λz1 ) . |
(1.3) |
|||||||
a |
|||||||||||||
Длина (модуль) вектора |
|
= ( x, y, z) |
вычисляется по формуле |
||||||||||
a |
|||||||||||||
|
|
|
|
|
= x 2 + y 2 + z 2 . |
(1.4) |
|||||||
|
|
а |
|
||||||||||
Скалярным произведением двух векторов a и b называется число, равное произведению длин этих векторов на косинус угла ϕ между ними:
a |
|
b |
= |
|
a |
|
|
|
b |
|
cosϕ . |
(1.5) |
Свойства скалярного произведения
1. |
|
a |
|
b |
= |
|
b |
|
|
a |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2. |
|
|
|
|
|
( |
|
|
|
|
|
+ |
|
|
|
|
|
) = |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
a |
b |
c |
a |
b |
a |
c |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. |
(λ |
|
|
|
|
|
|
) |
|
|
|
|
= (λ |
|
|
) |
|
|
= λ( |
|
|
|
) ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
a |
b |
b |
a |
a |
b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
|
= 0, если либо |
|
|
|
= 0 , либо |
|
= 0 , либо |
|
|
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
b |
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. |
|
|
|
|
|
|
= |
|
|
|
2 |
|
|
|
или |
|
|
2 = |
|
|
|
|
2 (скалярный квадрат вектора равен квадрату его |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
a |
a |
|
|
|
a |
|
a |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
длины, т.е. |
|
|
|
|
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
a |
a |
a |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пусть векторы |
|
( х1 , y1 , z1 ) и |
|
( х2 , y2 , z2 ) |
заданы своими координатами, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тогда скалярное произведение этих векторов находится по формуле |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= х1 х2 + y1 y2 + z1 z2 . |
(1.6) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||
4
