
NepDifPopovaSeljakova
.pdfВВЕДЕНИЕ
Математический анализ – одна из важнейших математических дисциплин. Хорошее знание математического анализа, глубокое понимание основных его идей и методов, умение решать задачи необходимы каждому математику.
Нужно также иметь в виду, что не зная анализа, нельзя овладеть большинством других математических курсов, изучаемых на математическом факультете. Понятия непрерывности и производной составляют наряду с понятием функции фундамент всего математического анализа.
Данные методические указания написаны для студентов первого курса специальности «Прикладная математика». Пособие содержит подробную программу по данной теме, теоретическую часть, проиллюстрированную примерами, вопросы для самоконтроля по сложности разного уровня. В пособии приведены образцы решения задач, индивидуальное задание и образец контрольной работы. Так как целесообразно исходить из одного лишь учебника и одного сборника задач, наши методические указания написаны применительно к книгам Кудрявцев Л. Д. Курс математического анализа Т. 1 и Кудрявцев Л. Д., Кутасов А. Д. Сборник задач по математическому анализу Т. 1. После изучения данной темы студенты должны уметь: исследовать функции на непрерывность, владеть техникой дифференцирования, применять производную для исследования функции на монотонность, нахождения локальных и глобальных экстремумов, интервалов выпуклости, асимптот, строить эскизы графиков функций, разлагать функции по формуле Тейлора и применять эту формулу при вычислении пределов и приближенных значений функций.
I. НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
1. Непрерывность функции в точке и на множестве ([1], 5.5; 5.12; 5.13)
1.1. Определение 1. Функция f x называется непрерывной в точке x0 ,
если она определена в этой точке и lim f x f x0 . |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение |
2. |
Если |
обозначить |
x x x0 , |
y f x f x0 , |
то |
|||||||||||||
определение непрерывной функции в точке |
x0 можно |
переформулировать, |
||||||||||||||||||
f x |
называется непрерывной в точке x0 |
, если lim f 0 . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
Определению 1 равносильно следующее (на языке « ”). |
|
|
|
||||||||||||||||
|
Определение |
3. |
f x |
называется |
непрерывной |
в точке |
x0 , если |
|||||||||||||
0 0 : x U x0, |
|
f x f x0 |
|
. |
|
|
f x |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
Определение |
4 (на языке последовательности). |
называется |
|||||||||||||||||
непрерывной в точке x0 , если xn x0 |
f xn f x0 . |
|
|
|
||||||||||||||||
|
Функцию |
f x , определенную на a, x0 , |
называют непрерывной слева в |
|||||||||||||||||
точке x0 , если |
lim |
f x f x0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функцию |
f x , определенную на x0 ;b , |
называют непрерывной справа |
|||||||||||||||||
в точке x0 , если |
lim |
f x f x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
Теорема 1 (Критерий непрерывности функции в точке). Для того чтобы |
|||||||||||||||||||
была непрерывной в точке x0 необходимо и достаточно чтобы она была |
||||||||||||||||||||
непрерывна и справа и слева. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Точки разрыва функции и их классификация |
|
|
|
|||||||||||||||
|
Определение 5. Пусть f x определена в окрестности точки x0 , кроме |
|||||||||||||||||||
быть может, самой точки x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Точку x0 называют точкой разрыва функции f |
в следующих случаях: |
|
|||||||||||||||||
|
1) |
f x не определена в этой точке; |
|
|
|
|
|
|
|
|
|
lim f x , |
|
|||||||
|
2) |
f x |
определена в |
точке x0 , |
но |
|
не |
существует |
но |
|||||||||||
lim f x f x0 . Если существует lim f x , |
|
|
|
|
|
|
|
|
x x0 |
|
|
|||||||||
но или |
f x не определена в точке |
|||||||||||||||||||
x x0 |
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
x0 , |
или |
lim |
f x |
lim f x f x0 , |
то |
точку |
x0 |
называют |
точкой |
|||||||||||
|
|
x x0 0 |
|
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
устранимого разрыва.
Если в точек x0 |
существуют lim f x и |
lim f x , но они не равны |
|
x x0 |
x x0 0 |
между собой, то точку |
x0 называют точкой разрыва 1-го рода, а разность |
|
f x0 0 f x0 0 называют скачком функции в точке x0 .
Если в точке x0 |
не существует хотябы один из пределов lim f x или |
|
x x0 0 |
lim f x , то называют точкой разрыва 2-го рода.
x x0 0
Примеры.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, если х рациональное, |
|||||
1) Рассмотрим функцию Дирихле D x |
|
|
|
|
Для |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
если х иррациональное. |
||||
x0 R не существует lim D x , поэтому точка x0 |
– точка разрыва 2-го рода. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
2) |
f x 2 |
|
, x 0 |
– |
точка разрыва |
2-го |
рода, так |
как |
lim 2 |
|
0 , |
||||||||
x |
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 0 |
||
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim 2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 0 0 |
|
|
|
|
|
|
1, x 0, |
|
|
|
|
|
|
|
|
||||
3) |
f x |
|
signx |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0, x 0, точка x 0 точка устранимого разрыва. |
||||||||||
|
|
|
f x x , x0 |
||||||||||||||||
4) |
1, lim |
f x 0; lim f x 1, точка x 0 |
– точка разрыва |
||||||||||||||||
1-го рода. |
x 1 0 |
x 1 0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1.2. Арифметические операции над непрерывными функциями |
||||||||||||||||||
Теорема 2. |
Если |
|
f x |
и g x |
непрерывны в |
точке x0 , то |
|||||||||||||
f x g x ; f x g x , c f x ; |
f x |
при |
g x |
0 также |
непрерывны в |
||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g x |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точке x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.3. Непрерывность элементарных функций |
|
|
|
|
|||||||||||||||
Определение. |
f x |
называется непрерывной на множестве Х, если f x |
|||||||||||||||||
непрерывна в каждой точке x X . |
|
|
ax , |
xa , loga x , |
|||||||||||||||
Основными элементарными функциями являются С, х, |
|||||||||||||||||||
sin x , cos x , arcsin x , |
arccos x . |
|
|
|
|
|
|
|
|
||||||||||
Элементарной функцией называют функцию, которая может быть задана с помощью конечного числа арифметических операций и суперпозиций из основных элементарных функций.
Теорема 3. все элементарные функции непрерывны в своей области определения.
2.Основные теоремы о непрерывных функциях
2.1.Локальные свойства непрерывной функции
Свойство |
|
1 (устойчивость). |
Если |
f x |
непрерывна |
в |
точке |
|
x0 |
и |
||||||||||||||||||||||||||||
f x0 0 , то существует окрестность точки x0 , |
в которой f x |
сохраняет знак |
||||||||||||||||||||||||||||||||||||
f x0 , т. е. |
sign |
f x sign f x0 . |
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Свойство 2 (ограниченность). |
Если |
|
непрерывна в точке |
|
x0 , |
то |
||||||||||||||||||||||||||||||||
существует окрестность точки x0 , в которой |
|
f x ограничена. |
|
|
|
|
x t |
|||||||||||||||||||||||||||||||
Свойство |
|
3 (непрерывность |
суперпозиции). Если функция |
|||||||||||||||||||||||||||||||||||
определена в окрестности точки t0 |
и непрерывна в |
t0 , t0 |
x0 , |
y f x |
||||||||||||||||||||||||||||||||||
определена в окрестности точки |
x0 |
и непрерывна в точке x0 , то существует |
||||||||||||||||||||||||||||||||||||
окрестность точки t0 , в которой определена суперпозиция f t |
непрерывная |
|||||||||||||||||||||||||||||||||||||
в точке t0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
Пример. Найти точки разрыва и определить их характер y |
|
|
|
|
, |
|||||||||||||||||||||||||||||||||
u2 u 2 |
||||||||||||||||||||||||||||||||||||||
где u |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x 1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
Функция |
u |
|
|
терпит |
|
разрыв в |
точке |
x 1. |
Функция |
||||||||||||||||||||||||||||
x 1 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y f u |
|
|
|
терпит разрыв в точках, |
где u2 u 2 0, т.е. |
u 2; u |
2 |
1 |
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
u2 u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
соответствующие значения x , решая |
|||||||||||||||||||||||||||
. По этим значениям и находим |
||||||||||||||||||||||||||||||||||||||
уравнения: 2 |
|
1 |
|
;1 |
|
1 |
; отсюда |
x |
1 |
|
и |
|
x 2 . Следовательно, сложная |
|||||||||||||||||||||||||
|
x 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
функция терпит разрыв в трех точках: |
x |
1 |
; x |
2 |
1; x |
2 . Выясним характер |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
разрывов в этих точках. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim y lim y 0 , поэтому x 1 – точка устранимого разрыва. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
x 0 |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
lim y lim y , lim y lim y , следовательно, точки |
x |
|
, x |
|
2 – |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
x |
1 |
|
|
|
u 2 |
|
|
|
|
x 2 |
u 1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точки разрыва 2-го рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2.2. Свойства функции непрерывной на отрезке |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Определение 6. Будем говорить, что |
|
f x |
непрерывна на отрезке a,b , |
|||||||||||||||||||||||||||||||||||
если она непрерывна на |
интервале a,b и непрерывна слева в точке b и |
|||||||||||||||||||||||||||||||||||||
непрерывна |
справа |
в |
точке |
a , |
|
т.е. |
|
x0 a,b |
lim f x f x0 |
и |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
lim f x f b ; lim f x f b .
x b 0 |
x b 0 |

Теорема 4 (Вейерштрасса 1. Об ограниченности). Если f x непрерывна на отрезке a,b , то она ограничена на a,b .
Теорема 5 (Вейерштрасса 2. О достижении функцией точной верхней и точной нижней грани). Если f x непрерывна на a,b , то она достигает на этом отрезке своей точной верхней и своей точной нижней грани, т.е. x a,b и x a,b такие, что f x sup f и f x inf f .
a,b |
a,b |
Теорема 6 (Больцано-Коши. Об обращении в нуль непрерывной |
|
функции). Если f x непрерывна на a,b и |
f a f b 0, то a,b такая, |
что f 0 .
Данная теорема используется для нахождения приближенного значения корня функциональногоуравнения f x 0 , а также позволяет обосновать метод интервалов при решении неравенств.
Теорема 7 (Больцано-Коши 2. О промежуточном значении непрерывной
функции). Если f x |
непрерывна на a,b и |
на концах отрезка принимает |
различные значения |
f a A ; f b B A B , то для любого С, лежащего |
|
между А и В, найдется точка a,b : f C . |
|
|
2.3. Существование и непрерывность обратной функции Определение 7. Пусть f взаимно однозначно отображает Х на Y , т.е.для
любых x1, x2 X из |
того, что x1 x2 , следует, что |
f x1 f x2 . Тогда |
для |
|||
каждого y Y найдется только одно значение x X такое, что f x y . |
|
|
||||
Отображение |
Y |
на Х называют обратной |
функцией для |
|
|
и |
|
|
|||||
обозначают , т.е. x f |
1 y , y Y . |
|
|
|
|
|
Теорема 8 (О существовании и непрерывности обратной функции). Пусть f x определена, строго возрастает (убывает) и непрерывна на a,b . Тогда она имеет обратную функцию, которая определена, строго возрастает (убывает) и непрерывна на f a , f b (соответственно f b , f a ).
Теорема |
9. Пусть f x |
определена, |
строго |
возрастает (убывает) и |
|
непрерывна на |
a,b , и пусть |
c lim |
f x , |
d lim |
f x . Тогда она имеет |
|
|
x a 0 |
|
x b 0 |
|
обратную функцию, которая определена, строго возрастает (убывает) и непрерывна на c, d (соответственно d,c ).
Вопросы для самоконтроля
1. Сформулировать на языке « » определение непрерывной 1) слева,
2) справа в точке x0 функции и записать его, используя символы , .
2.Сформулировать определение непрерывной в точке функции на языке последовательностей.

3. f x непрерывна в точке x0 , и в любой окрестности этой точки имеются как значения х, в которых функция положительна, так и значения х, в которых функция отрицательна. Найти f x0 .
4. Пусть f x определена в окрестности точки x0 . Сформулировать, используя символы , , утверждение, что функция не является непрерывной в
точке x0 .
5. Обязательно ли будет разрывна в точке x0 сумма двух функций f x g x , если:
а) f x непрерывна в точке x0 , а g x разрывна; б) обе функции f x и g x разрывны в точке x0 ? Привести соответствующие примеры.
6.Можно ли утверждать, что квадрат разрывной функции есть также разрывная функция?
7.Привести пример функции, непрерівной на каждом из промежутков X1 и X2 ,
но не являющейся непрерівной на множестве X1 X 2 .
8.Привести пример непрерівной на интервале функции: 1) неограниченной на єтом интервале; 2) ограниченной на єтом интервале, но не достигающей ни своей верхней, ни нижней грани.
9.Доказать, что если функция определена и непрерівна на отрезке, то множество ее значений – отрезок.
10.Привести пример разрівной функции, определенной на отрезке и имеющей
вкачестве множества значений отрезок.
11. |
Функция |
f x |
непрерівна на |
a; , и существует |
конечный |
lim f x . |
|
Доказать, что |
f ограничена на a; . |
|
x |
||
|
|
lim f x и |
||||
12. |
Функция |
f x |
непрерывна на |
a,b , и существуют конечные |
||
|
lim f x . Доказать, что f x ограничена на a,b . |
|
x a |
|||
|
|
|
||||
13. |
x b |
|
|
f x : 1) определена и |
монотонна на a,b ; |
|
Доказать, что если функция |
||||||
|
2) принимает все промежуточные значения между |
f a и f b , то она |
||||
|
непрерывна на a,b . |
|
|
|
||
Образец тестового задания по теме «Непрерывность функции»
Какие утверждения справедливы:
1)f x непрерывна в промежутке 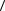 a,b
a,b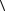 f x ограничена в
f x ограничена в 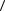 a,b
a,b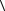 ;
;
2)f x не имеет нулей в 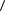 a,b
a,b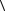 f x сохраняет знак в
f x сохраняет знак в 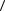 a,b
a,b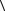 ;
;
3)f x непрерывна и не имеет нулей в промежутке 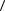 a,b
a,b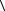 f x
f x
знакопостоянна в 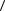 a,b
a,b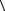 ;
;
4) |
f x непрерывна на a,b и x0 a,b , где |
f x0 0 x1 |
и x2 a,b , где |
|
f x1 f x2 0 . |
|
|
5) |
f x непрерывна на a,b Y f x c, d ; |
|
|

6)f x органичена на a,b f x непрерывна на a,b ?
II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
1.Три основных понятия дифференциального исчисления
1.1. Понятие производной. Геометрический и физический смысл
Определение |
8. Пусть |
функция |
y f x определена в некоторой |
окрестности точки |
x0 U x0 , |
и пусть |
x0 x U x0 , . Предел отношения |
приращения функции в точке к приращению аргумента при x 0 называется производной функции в точке.
f x0 |
lim |
y |
lim |
f x0 |
|
lim |
f x0 x f x0 |
. |
|
x |
|
||||||
|
x 0 x |
x 0 |
x 0 |
x |
||||
Другие обозначения производной df x0 ; dy . dx dx
Геометрический смысл |
приоизводной. Если функция y |
f x имеет |
|
производную в точке x0 , то |
угловой |
коэффициент касательной |
к графику |
функции в точке M x0 ; f x0 |
равен |
f x0 . Уравнение касательной в точке |
|
M x0 ; f x0 имеет вид y f x0 f x0 x x0 . |
y f x в |
||
Механический смысл производной. Производная функции |
|||
точке x0 есть скорость изменения функции.
1.2. Понятие дифференцируемости. Критерий дифференцируемости
Определение 9. |
Функция |
y f x , определенная |
в некоторой |
окрестности U x0 точки x0 , называется дифференцируемой при |
x x0 , если ее |
||
приращение в этой |
точке, т.е. |
f x0 f x0 x f x0 , |
x0 x U x0 , |
представим в виде f x0 A x o x A x x x , где А – постоянная,
x 0
lim x 0 .
x 0
Связь между дифференцируемостью функции в точке и существованием производной в этой же точке устанавливает следующая теорема.
Теорема 10. Для того чтобы функция f x была дифферецируемой в точке x0 , необходимо и достаточно. Чтобы она имела в этой точке производную, при этом f x0 A из определения 9.
Таким образом, дифференцируемость функции в точке равносильна существованию в этой точке конечной производной.
Выясним связь между дифференцируемостью и непрерывностью в точке.

Теорема 11. Если функция f x дифференцируема в точке, то она и непрерывна в этой точке.
Замечание. Обратная теорема неверна, из непрерывности f x в точке не следует ее дифференцируемость или, что равносильно, существование производной в этой точке.
1.3. Понятие дифференциала. Геометрический и физический смысл
Определение |
10. |
Пусть f x |
дифференцируема в точке x0 , |
||
дифференциалом функции |
f в точке x0 |
называется главная линейная часть |
|||
A x приращения функции в этой точке, обозначается df x0 или dy |
|
x x0 . |
|||
|
|||||
|
|||||
Таким образом, df x0 A x. |
в точке функции A f x0 , то |
||||
Так как для |
дифференцируемой |
||||
df x0 f x0 dx , dx x .
Геометрический смысл дифференциала. Поскольку уравнение касательной y f x0 f x0 x x0 и дифференциала dy f x0 x имеют одинаковую правую часть, то геометрический смысл дифференциала – приращение ординаты касательной y y f x0 .
|
1.4. Односторонние и бесконечные производные |
|
|
||||||||||||
|
Определение |
|
|
11. Если функция |
|
|
f x |
определена в некоторой |
|||||||
правосторонней (левосоронней) окрестности точки |
x0 |
и существует |
предел |
||||||||||||
|
f x |
0 |
x f x |
0 |
|
|
f x x f x |
0 |
|
|
|
|
|
||
lim |
|
|
|
|
lim |
0 |
|
, |
то |
он |
называется |
правой |
|||
|
|
x |
|
|
|
x |
|
|
|||||||
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|||
(левой) производной f x в точке x0 и обозначается |
|
|
f x0 |
f x0 . |
|
Правая и левая производные называются односторонними производными. |
||
Теорема 12. Для того чтобы функция y f x , определенная в некоторой |
||
окрестности точки x0 имела производную f x0 , |
необходимо и достаточно, |
|
чтобы существовали односторонние производные в точке x0 и они были равны f x0 f x0 .
|
Определение |
12. |
Если |
для |
некоторого |
значения |
x0 |
|
lim |
f x0 |
x f x0 |
, то |
говорят, |
что |
функция f x |
в точке x0 |
имеет |
|
x |
|||||||
x 0 |
|
|
|
|
|
|
||
бесконечную производную.
Пример. f x 3  x, x0 0.
x, x0 0.
|
f x f 0 |
|
3 |
x |
|
|
1 |
. |
|
|
|
lim |
|
|
lim |
|
|
||
Решение. f 0 lim |
x |
x |
|
||||||
x 0 |
x 0 |
x 0 3 x2 |
|
||||||
2.Правила дифференцирования
2.1.Дифференцирование арифметических операций
|
|
|
Тероема 13. Если функции |
|
f x |
и g x дифференцируемы в точке x0 , то |
|||||||||||||||||
и их сумма f x g x , произведение |
|
|
f x g x , а если g x 0 , то и частное |
||||||||||||||||||||
|
f x |
дифференцируемы в точке x0 , причем |
|
|
|
|
|
|
|
||||||||||||||
|
g x |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
c |
|
f |
|
c const , |
|
|
||||||||||
|
|
|
|
c f |
|
, |
|
|
|||||||||||||||
|
|
|
|
|
f |
|
|
|
|
|
f g |
, |
|
|
|
|
|
||||||
|
|
|
|
|
g |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
f g f g , |
|
|
|||||||||||
|
|
|
|
f g |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
g f g |
|
|
|||||||||||||||
|
|
|
|
|
f |
|
|
f |
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
||||||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Следствие. При выполнении условий теоремы имеем: |
|
|||||||||||||||||||
|
|
|
|
d c f c df , |
|
c const , |
|
|
|||||||||||||||
|
|
|
|
d f g df dg , |
|
|
|||||||||||||||||
|
|
|
|
d f g g df f dg , |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
d |
f |
|
|
g df f dg |
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
2 |
|
|
|
|
|
|
||||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2.2. Дифференцирование сложной функции |
|
|
||||||||||||||||||
|
|
|
Теорема 14. |
Пусть x t дифференцируема |
в точке t0 , а |
y f x |
|||||||||||||||||
дифференцируема |
в точке |
|
x0 t0 , |
тогда |
суперпозиция |
f t |
|||||||||||||||||
дифференцируема в точке t0 , причем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
fx x0 t t0 |
fx x0 xt t0 . |
|
|||||||||||||||
|
|
|
|
f t t t0 |
|
|
|||||||||||||||||
Данная теорема распространяется на любое конечное число суперпозиций.
2.3. Дифференцирование обратной функции
Теорема 15. Пусть функция y f x непрерывна и строго монотонна в некоторой окрестности точки x0 , и пусть в этой точке существует производная
|
df x0 |
0 ; |
тогда обратная |
функция x f 1 y |
имеет производную в точке |
||||||||||
|
|
||||||||||||||
|
dx |
|
df 1 y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 f x0 , |
причем |
|
1 |
|
|
, т.е. производная обратной функции равна |
||||||||
|
|
df x0 |
|||||||||||||
|
|
|
|
dy |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
обратной величине производной данной функции. |
|
||||||||||||||
|
Пример. y arcsin x, |
x sin y; |
|
|
y |
|
; |
1 x 1. |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||

Решение. Выполнены все условия теоремы.
|
|
1 |
|
1 |
|
1 |
|
|
|
|
1 |
|
1 |
|
||
arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos arcsin x |
|
|
|
|
|
|
|
|||||||
cos y |
1 sin |
2 |
arcsin x |
1 x |
2 |
|||||||||||
|
|
sin y |
|
|
|
|
|
|
||||||||
x 1;1 .
2.4. Инвариантность формы первого дифференциала
Формула для дифференциала dy f x dx справедлива и в том случае,
когда х |
является не независимой переменной x x t , в этом случае |
dx x t dt |
dt t , а если х – независимая переменная, то dx x const . Это |
свойство называется свойством инвариантности формы дифференциала.
2.5. Дифференцируемость простейших элементарных функций
1)c 0, c const .
2)x x 1, x 0, R .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) ax ax ln a, x R, a 0, a 1. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
x R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4) ex ex , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) loga x |
|
|
|
|
|
|
|
|
|
|
, x 0, a 0, a 1. |
||||||||||||||||||||
|
x ln a |
||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6) ln x |
|
|
, |
|
x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos x, |
|
|
x R . |
|
|
||||||||||||||||||||||||||
7) sin x |
|
|
|
|
|||||||||||||||||||||||||||
|
sin x, x R . |
|
|
||||||||||||||||||||||||||||
8) cos x |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9) tgx |
|
|
|
|
, |
|
|
x |
|
|
2n 1 , |
n Z . |
|||||||||||||||||||
cos2 x |
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10) ctgx |
|
|
|
|
|
|
|
|
|
|
, |
x n, n Z . |
|||||||||||||||||||
|
|
sin2 |
x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11) arcsin x |
|
|
|
|
|
|
|
|
|
, |
|
|
x |
|
|
1. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
12) arccos x |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
x |
|
1. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
1 x2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
13) arctgx |
|
|
|
, |
x R . |
|
|
||||||||||||||||||||||||
1 x2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14) arcctgx |
|
|
, |
|
|
x R . |
|
|
|||||||||||||||||||||||
1 x2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
e x |
|
15) shx |
chx, x |
R; |
shx |
|
|
гиперболический синус . |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
2
