
Metodichka_lab_Ekonometria
.pdf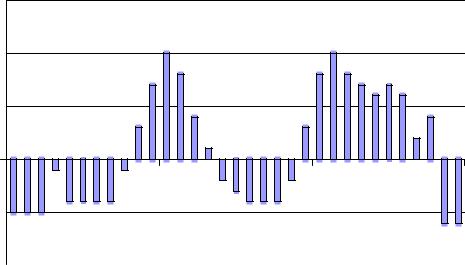
|
1,5 |
Коррелограмма |
|
автокорреляции |
|
|
|
1 |
|
|
|
0,5 |
|
|
|
|
|
|
|
Коэффициент |
0 |
|
|
1 |
12 |
23 |
|
-0,5 |
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
Лаг |
|
|
|
Рис. 9.9 – Коррелограмма |
|
Из графика коррелограммы видно, что в данных имеется годовая сезонная составляющая.
Рассмотрим аддитивную и мультипликативную модели, сравним их качество.
Предположим наличие аддитивной взаимосвязи между компонентами ряда, т. е.
Y =Q + S +ε. |
(9.18) |
1. Сглаживаем исходный временной ряд методом центрированной скользящей средней, используя формулу для месячных данных
yt = |
1 |
|
yt−6 |
+ yt −5 + yt−4 |
+ yt −3 + yt −2 + yt−1 + yt + |
|||||||
|
|
|
||||||||||
% |
|
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.19) |
|||
|
|
|
|
|
|
|
|
|
|
|
yt +6 |
|
+y |
+ y |
|
+ y |
|
+ y |
+ y |
|
+ |
(t = 7,8, ..., n −7). |
|||
|
|
|
|
|||||||||
t +1 |
|
t+2 |
t+3 |
t +4 |
t +5 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Результаты вычислений |
yij |
вносим в табл. 9.6. Сглаженные данные |
||||||||||
|
|
|
|
|
|
|
|
% |
|
|
|
|
находятся в пятом столбце этой таблицы. |
||||||||||||
В таблице i −номер года; |
|
|
j −номер месяца в году (каждой паре |
|||||||||
номеров i, j соответствует один номер t ).
2. Находим оценки сезонной вариации. Для этого из уровней исходного временного ряда вычитаем сглаженные значения
eij = yij − yij |
(9.20) |
%
и записываем их в шестом столбце табл. 9.6. Заполняем табл. 9.6.
129
Таблица 9.6
Расчёты аддитивной модели
Наблюдения |
годаНомер |
годувмесяцаНомер |
Потребляемая электроэнергия |
Сглаженные yзначения |
сезоннойОценка сезонная(вариациии случайная )компонента |
Сезонная составляяющая |
–Десезона исходныелизованные данные |
значенияТрендовые |
случайЗначения– ной компоненты |
–Относитель ошибканая |
|||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
||
t |
i |
j |
yij |
y%ij |
eij = yij − y%ij |
S j |
qij = yij − S j |
qˆij |
εij |
ε |
ij |
|
/ y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
1 |
1 |
153 |
|
|
–13,3 |
166,3 |
171,8 |
–5,4 |
0,036 |
|||
2 |
1 |
2 |
136 |
|
|
–37,5 |
173,5 |
173,0 |
0,5 |
0,004 |
|||
3 |
1 |
3 |
153 |
|
|
–24,2 |
177,2 |
174,2 |
3,0 |
0,020 |
|||
4 |
1 |
4 |
158 |
|
|
–19,1 |
177,1 |
175,3 |
1,7 |
0,011 |
|||
5 |
1 |
5 |
151 |
|
|
–30,9 |
181,9 |
176,5 |
5,4 |
0,036 |
|||
6 |
1 |
6 |
178 |
|
|
–5,5 |
183,5 |
177,7 |
5,8 |
0,032 |
|||
7 |
1 |
7 |
174 |
180,96 |
–6,96 |
–11,0 |
185,0 |
178,9 |
6,2 |
0,035 |
|||
8 |
1 |
8 |
178 |
182,54 |
–4,54 |
–6,0 |
184,0 |
180,1 |
3,9 |
0,022 |
|||
9 |
1 |
9 |
211 |
183,88 |
27,13 |
27,8 |
183,2 |
181,2 |
2,0 |
0,009 |
|||
10 |
1 |
10 |
233 |
185,00 |
48,00 |
52,0 |
181,0 |
182,4 |
–1,4 |
0,006 |
|||
11 |
1 |
11 |
234 |
185,83 |
48,17 |
55,1 |
178,9 |
183,6 |
–4,7 |
0,020 |
|||
12 |
1 |
12 |
202 |
186,29 |
15,71 |
12,7 |
189,3 |
184,8 |
4,5 |
0,022 |
|||
13 |
1 |
1 |
174 |
186,42 |
–12,42 |
–13,3 |
187,3 |
186,0 |
1,4 |
0,008 |
|||
14 |
1 |
2 |
153 |
186,58 |
–33,58 |
–37,5 |
190,5 |
187,2 |
3,4 |
0,022 |
|||
15 |
1 |
3 |
168 |
187,04 |
–19,04 |
–24,2 |
192,2 |
188,3 |
3,9 |
0,023 |
|||
16 |
1 |
4 |
170 |
187,88 |
–17,88 |
–19,1 |
189,1 |
189,5 |
–0,4 |
0,003 |
|||
17 |
1 |
5 |
159 |
189,21 |
–30,21 |
–30,9 |
189,9 |
190,7 |
–0,8 |
0,005 |
|||
18 |
1 |
6 |
181 |
190,00 |
–9,00 |
–5,5 |
186,5 |
191,9 |
–5,4 |
0,030 |
|||
19 |
1 |
7 |
174 |
190,25 |
–16,25 |
–11,0 |
185,0 |
193,1 |
–8,0 |
0,046 |
|||
20 |
1 |
8 |
182 |
190,58 |
–8,58 |
–6,0 |
188,0 |
194,2 |
–6,2 |
0,034 |
|||
21 |
1 |
9 |
218 |
190,71 |
27,29 |
27,8 |
190,2 |
195,4 |
–5,2 |
0,024 |
|||
22 |
1 |
10 |
246 |
191,17 |
54,83 |
52,0 |
194,0 |
196,6 |
–2,6 |
0,011 |
|||
23 |
1 |
11 |
253 |
192,08 |
60,92 |
55,1 |
197,9 |
197,8 |
0,1 |
0,000 |
|||
24 |
1 |
12 |
202 |
193,50 |
8,50 |
12,7 |
189,3 |
199,0 |
–9,6 |
0,048 |
|||
25 |
1 |
1 |
180 |
195,42 |
–15,42 |
–13,3 |
193,3 |
200,2 |
–6,8 |
0,038 |
|||
26 |
1 |
2 |
155 |
197,58 |
–42,58 |
–37,5 |
192,5 |
201,3 |
–8,8 |
0,057 |
|||
27 |
1 |
3 |
169 |
199,50 |
–30,50 |
–24,2 |
193,2 |
202,5 |
–9,3 |
0,055 |
|||
28 |
1 |
4 |
180 |
201,42 |
–21,42 |
–19,1 |
199,1 |
203,7 |
–4,6 |
0,026 |
|||
29 |
1 |
5 |
171 |
203,71 |
–32,71 |
–30,9 |
201,9 |
204,9 |
–3,0 |
0,017 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|
Продолжение таблицы 9.6
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
30 |
1 |
6 |
203 |
206,08 |
–3,08 |
–5,5 |
208,5 |
206,1 |
2,4 |
0,012 |
31 |
1 |
7 |
198 |
|
|
–11,0 |
209,0 |
207,2 |
1,8 |
0,009 |
32 |
1 |
8 |
210 |
|
|
–6,0 |
216,0 |
208,4 |
7,6 |
0,036 |
33 |
1 |
9 |
236 |
|
|
27,8 |
208,2 |
209,6 |
–1,4 |
0,006 |
34 |
1 |
10 |
274 |
|
|
52,0 |
222,0 |
210,8 |
11,2 |
0,041 |
35 |
1 |
11 |
280 |
|
|
55,1 |
224,9 |
212,0 |
12,9 |
0,046 |
36 |
1 |
12 |
232 |
|
|
12,7 |
219,3 |
213,1 |
6,2 |
0,027 |
|
|
|
|
|
|
|
|
|
Σ = |
0,877 |
Eотн. ошиб. = 0,877/36 100 %=2,436 % .
3. Определяем сезонные составляющие.
Сезонная вариация – это повторение данных через небольшой промежуток времени. Под «сезоном» можно понимать день, неделю, месяц, квартал, год. Если же промежуток времени сезонной волны будет длительным, то это будет циклическая вариация.
Заполняем вспомогательную табл. 9.7. Оценки сезонной вариации записываем под соответствующим номером месяца в году.
4. Усредняем полученные значения eij за все годы по каждому
месяцу: сумму чисел в столбце, например, выделенных жирным шрифтом, делим на количество чисел в столбце. Сумма чисел в строке еj равна –
6,81.
5. Корректируем средние значения еj , увеличивая или уменьшая их на
одно и то же число так, чтобы их сумма была равна нулю. В результате получим «выправленную» сезонную волну. В нашем примере из чисел в строке
еj |
под номерами кварталов вычитаем число − 0,57 = |
− 6,8 |
. В последней строке |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
S j для |
|
получены |
значения |
скорректированной |
сезонной |
вариации |
|||||||||||||||
соответствующегомесяцагода. |
|
|
|
|
|
|
|
|
Таблица 9.7 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Определение сезонной составляющей в аддитивной модели |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер месяца в году |
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
|
11 |
12 |
|
|
|
|
|
–12,4 |
|
–33,6 |
–19,0 |
–17,9 |
–30,2 |
–9,0 |
–7,0 |
–4,5 |
27,1 |
48,0 |
48,2 |
15,7 |
|
|
||
|
|
|
–15,4 |
|
–42,6 |
–30,5 |
–21,4 |
–32,7 |
–3,1 |
–16,3 |
–8,6 |
27,3 |
54,8 |
60,9 |
8,5 |
|
|
||
|
e |
j |
–13,9 |
|
–38,1 |
–24,8 |
–19,7 |
–31,5 |
–6,0 |
–11,6 |
–6,6 |
27,2 |
51,4 |
54,5 |
12,1 |
–6,8 |
–0,57 |
||
S j |
–13,4 |
|
–37,5 |
–24,2 |
–19,1 |
–30,9 |
–5,5 |
–11,0 |
–6,0 |
27,8 |
52,0 |
55,1 |
12,7 |
0,0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
131 |
|
6. Проведём десезонализацию исходных данных: вычтем соответствующие значения сезонной компоненты из фактических
значений уровней ряда за каждый месяц, т. е. |
|
qij = yij − S j . |
(9.21) |
Вычисленные таким образом значения ряда состоят из тренда и случайной компоненты, столбец 6.
7. По методу наименьших квадратов рассчитываем для полученного ряда кривую роста, аппроксимирующую ряд
ˆ |
(9.22) |
Q =170,61 +1,1816t . |
По кривой роста (9.22) вычисляем qˆij , подставляя в (9.22) t =1,2,3,...,
столбец 9 табл. 9.6.
8. Определяем значение случайной компоненты
εij = yij − qˆij − S j . |
(9.23) |
9. Вычисляем прогнозные значения потребления электроэнергии на четыре месяца следующего года, табл. 9.8.
Таблица 9.8
Определение прогноза по аддитивной модели
Месяц |
j |
Тренд, qˆ4 j |
S j |
Прогноз, yˆ4 j |
37 |
1 |
214,3 |
–13,3 |
201,0 |
38 |
2 |
215,5 |
–37,5 |
178,0 |
39 |
3 |
216,7 |
–24,2 |
192,5 |
40 |
4 |
217,9 |
–19,1 |
198,8 |
Прогнозные значения вычисляются следующим образом:
yˆ |
= yˆ |
( Прогноз) = yˆ |
4 j |
= yˆ |
2010 |
j |
= qˆ |
4 j |
+ S |
j |
( j =1,2,3) ; |
36+ j |
|
4 j |
|
|
|
|
yˆ37 = yˆ41 = yˆ01.01.12 = 170,61 +1,18 37 -13,3 =201,0 ;
yˆ38 = yˆ42 = yˆ01.02.12 = 170,61 +1,18 38-37,5=178,0;
yˆ39 = yˆ43 = yˆ01.03.12 = 170,61 +1,18 39 -24,2=192,5;
yˆ40 = yˆ44 = yˆ01.04.12 = 170,61 +1,18 39 -19,1=198,8 .
132
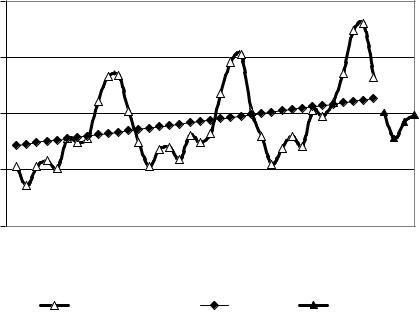
Строим графики исходного ряда, тренда и прогноза на следующие |
||||||
четыре месяца, рис. 9.10. |
|
|
|
|
||
электроэнергии |
300 |
|
|
|
|
|
250 |
|
|
|
|
||
200 |
|
|
|
|
||
|
|
|
|
|
||
Потребление |
150 |
|
|
|
|
|
100 |
|
|
|
|
||
0 |
10 |
20 |
30 |
40 |
||
|
||||||
|
|
|
Месяцы |
|
|
|
|
|
Исходный ряд |
Тренд |
|
Прогноз |
|
Рис. 9.10 – Прогноз при наличии сезонной составляющей в аддитивной модели
Предположим наличие мультипликативной взаимосвязи между компонентами ряда, т. е.
Y = Q S ε. |
(9.24) |
1.Сглаживаем исходный временной ряд методом центрированной скользящей средней, используя формулу (9.19) для месячных данных
Результаты вычислений вносим в табл. 9.9. Сглаженные данные находятся в пятом столбце этой таблицы.
2.Проводим оценку сезонной вариации. Делим значения исходного временного ряда на соответствующие сглаженные значения ряда
eij = yij / yij . |
(9.25) |
% |
|
Результаты записываем в шестом столбце табл. 9.9.
133

Таблица 9.9
Расчёты мультипликативной модели
Наблюдения, t годаНоме, i месяцаНомев году, j Потребление электроэнергии, y |
Сглаженные значенияy |
сезоннойОценка вариации(сезонная и случайная компонента) Сезонная составляющая |
Десезонализованные исходныеданные |
Трендовыезначения |
Значенияслучайной компоненты |
Относительная ошибка |
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
t |
i |
j |
yij |
% |
eij |
= |
% |
S j |
qij |
= |
yij / S j |
ˆ |
ε |
ij |
|
εij |
|
/ yij |
|
|
|||||||||||||||||
yij |
|
yij / yij |
|
qij |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
1 |
1 |
153 |
|
|
|
|
0,93 |
|
164,8 |
171,6 |
–6,4 |
0,042 |
|||||
2 |
1 |
2 |
136 |
|
|
|
|
0,80 |
|
169,3 |
172,8 |
–2,8 |
0,021 |
|||||
3 |
1 |
3 |
153 |
|
|
|
|
0,87 |
|
175,1 |
173,9 |
1,0 |
0,007 |
|||||
4 |
1 |
4 |
158 |
|
|
|
|
0,90 |
|
175,5 |
175,1 |
0,3 |
0,002 |
|||||
5 |
1 |
5 |
151 |
|
|
|
|
0,84 |
|
179,5 |
176,3 |
2,8 |
0,018 |
|||||
6 |
1 |
6 |
178 |
|
|
|
|
0,97 |
|
183,5 |
177,4 |
5,9 |
0,033 |
|||||
7 |
1 |
7 |
174 |
180,96 |
|
0,96 |
0,94 |
|
185,2 |
178,6 |
6,3 |
0,036 |
||||||
8 |
1 |
8 |
178 |
182,54 |
|
0,98 |
0,97 |
|
184,2 |
179,7 |
4,3 |
0,024 |
||||||
9 |
1 |
9 |
211 |
183,88 |
|
1,15 |
1,15 |
|
184,0 |
180,9 |
3,5 |
0,017 |
||||||
10 |
1 |
10 |
233 |
185,00 |
|
1,26 |
1,27 |
|
182,8 |
182,0 |
0,9 |
0,004 |
||||||
11 |
1 |
11 |
234 |
185,83 |
|
1,26 |
1,29 |
|
181,4 |
183,2 |
–2,3 |
0,010 |
||||||
12 |
2 |
12 |
202 |
186,29 |
|
1,08 |
1,07 |
|
189,6 |
184,4 |
5,6 |
0,027 |
||||||
13 |
2 |
1 |
174 |
186,42 |
|
0,93 |
0,93 |
|
187,4 |
185,5 |
1,7 |
0,010 |
||||||
14 |
2 |
2 |
153 |
186,58 |
|
0,82 |
0,80 |
|
190,5 |
186,7 |
3,0 |
0,020 |
||||||
15 |
2 |
3 |
168 |
187,04 |
|
0,90 |
0,87 |
|
192,3 |
187,8 |
3,9 |
0,023 |
||||||
16 |
2 |
4 |
170 |
187,88 |
|
0,90 |
0,90 |
|
188,8 |
189,0 |
–0,2 |
0,001 |
||||||
17 |
2 |
5 |
159 |
189,21 |
|
0,84 |
0,84 |
|
189,1 |
190,2 |
–0,9 |
0,006 |
||||||
18 |
2 |
6 |
181 |
190,00 |
|
0,95 |
0,97 |
|
186,6 |
191,3 |
–4,6 |
0,025 |
||||||
19 |
2 |
7 |
174 |
190,25 |
|
0,91 |
0,94 |
|
185,2 |
192,5 |
–6,8 |
0,039 |
||||||
20 |
2 |
8 |
182 |
190,58 |
|
0,95 |
0,97 |
|
188,3 |
193,6 |
–5,1 |
0,028 |
||||||
21 |
2 |
9 |
218 |
190,71 |
|
1,14 |
1,15 |
|
190,1 |
194,8 |
–5,4 |
0,025 |
||||||
22 |
2 |
10 |
246 |
191,17 |
|
1,29 |
1,27 |
|
193,0 |
195,9 |
–3,8 |
0,015 |
||||||
23 |
2 |
11 |
253 |
192,08 |
|
1,32 |
1,29 |
|
196,1 |
197,1 |
–1,2 |
0,005 |
||||||
24 |
2 |
12 |
202 |
193,50 |
|
1,04 |
1,07 |
|
189,6 |
198,3 |
–9,2 |
0,046 |
||||||
25 |
3 |
1 |
180 |
195,42 |
|
0,92 |
0,93 |
|
193,9 |
199,4 |
–5,2 |
0,029 |
||||||
26 |
3 |
2 |
155 |
197,58 |
|
0,78 |
0,80 |
|
193,0 |
200,6 |
–6,1 |
0,039 |
||||||
27 |
3 |
3 |
169 |
199,50 |
|
0,85 |
0,87 |
|
193,4 |
201,7 |
–7,3 |
0,043 |
||||||
28 |
3 |
4 |
180 |
201,42 |
|
0,89 |
0,90 |
|
199,9 |
202,9 |
–2,7 |
0,015 |
||||||
134

Продолжение таблицы 9.9
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
29 |
3 |
5 |
171 |
203,71 |
0,84 |
|
0,84 |
203,3 |
204,0 |
–0,6 |
0,004 |
30 |
3 |
6 |
203 |
206,08 |
0,99 |
|
0,97 |
209,3 |
205,2 |
3,9 |
0,019 |
31 |
3 |
7 |
198 |
|
|
|
0,94 |
210,8 |
206,4 |
4,2 |
0,021 |
32 |
3 |
8 |
210 |
|
|
|
0,97 |
217,3 |
207,5 |
9,5 |
0,045 |
33 |
3 |
9 |
236 |
|
|
|
1,15 |
205,8 |
208,7 |
–3,3 |
0,014 |
34 |
3 |
10 |
274 |
|
|
|
1,27 |
214,9 |
209,8 |
6,5 |
0,024 |
35 |
3 |
11 |
280 |
|
|
|
1,29 |
217,1 |
211,0 |
7,8 |
0,028 |
36 |
3 |
12 |
232 |
|
|
|
1,07 |
217,7 |
212,1 |
5,9 |
0,026 |
|
|
|
|
|
|
|
|
|
|
Σ =0,790 |
|
|
|
|
|
E |
|
= 0,790 100 %=2,2 % . |
|
|
|||
|
|
|
|
отн. ошиб. |
36 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
3. Определяем сезонные составляющие.
Заполняем табл. 9.10. Оценки сезонной вариации записываем в столбце соответственно номеру месяца в году.
Таблица 9.10
Определение сезонной составляющей в мультипликативной модели
|
|
|
|
|
|
|
Номер месяца в году |
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
2 |
3 |
4 |
|
5 |
6 |
|
7 |
8 |
|
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,93 |
0,82 |
0,90 |
0,90 |
0,84 |
0,95 |
0,96 |
0,98 |
1,15 |
1,26 |
1,26 |
1,08 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,92 |
0,78 |
0,85 |
0,89 |
0,84 |
0,99 |
0,91 |
0,95 |
1,14 |
1,29 |
1,32 |
1,04 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
j |
0,93 |
0,80 |
0,87 |
0,90 |
0,84 |
0,97 |
0,94 |
0,96 |
1,15 |
1,27 |
1,29 |
1,07 |
|
11,98 |
0,9987 |
|
|||
e |
|
||||||||||||||||||||
S j |
0,93 |
0,80 |
0,87 |
0,90 |
0,84 |
0,97 |
0,94 |
0,97 |
1,15 |
1,27 |
1,29 |
1,07 |
|
12,00 |
|
|
|||||
4. |
Усредняем |
полученные |
значения eij за |
все |
годы |
по каждому |
|||||||||||||||
месяцу: сумму чисел в каждом столбце, делим на количество чисел в этом столбце. Сумма чисел в строке ej равна 11,98 (см. табл. 9.10).
5. Корректируем средние значения ej . Значение сезонной вариации –
это доли при числе двенадцати месяцев, а поэтому необходимо, чтобы сумма средних была равна 12. Следовательно, итоговые коэффициенты
сезонности нужно поделить на число 0,998666 = 11,9812 . В последней строке
табл. 9.10 указаны окончательные коэффициенты сезонности – значения сезонной вариации для соответствующего месяца года.
135
6. Проведём десезонализацию исходных данных: исходные уровни временного ряда делим на соответствующие скорректированные значения сезонной компоненты, т. е. qij = yij / S j (восьмой столбец табл. 9.9).
Вычисленные таким образом значения ряда состоят из тренда и случайной компоненты.
7. Подбираем для полученного ряда кривую роста, аппроксимирующую ряд. Она будет иметь следующий вид:
ˆ |
=170,47+1,158 t |
(9.26) |
Q |
8. Определяем значение случайной компоненты (10–й столбец табл. 9.9) по формуле εij = yij − qˆij S j и относительную ошибку (11–й столбец
табл. 9.9)
|
1 |
3 4 |
|
εij |
|
1 |
|
Eотн. ошиб. = |
|
∑∑ |
|
|
100 % = |
|
0,790 100 % = 2,2 %. |
36 |
|
y |
36 |
||||
|
|
j=1 i=1 |
|
ij |
|
|
|
(9.27)
9. Вычисляем прогнозные значения на четыре месяца следующего года
yˆ |
+ j |
= yˆ |
(прогноз) = yˆ |
4 j |
= yˆ |
= qˆ |
S |
j |
( j =1,2,3.4) ; |
|||||||
36 |
|
4 j |
|
|
01.0j.12 |
4 j |
|
|
|
|
|
|
|
|||
ˆ |
= |
ˆ |
= |
ˆ |
= |
(170,47+1,1577 |
|
37) |
|
0,93=198,1; |
||||||
y37 |
|
y41 |
|
y01.01.12 |
|
|
|
|
||||||||
ˆ |
= |
ˆ |
= |
ˆ |
= |
(170,47+1,1577 |
|
38) |
|
0,80=172,3 |
; |
|||||
y38 |
|
y42 |
|
y01.02.12 |
|
|
|
|
||||||||
ˆ |
= |
ˆ |
= |
ˆ |
= |
(170,47+1,1577 |
|
39) |
|
0,87=188,4 |
; |
|||||
y39 |
|
y43 |
|
y01.03.12 |
|
|
|
|
||||||||
ˆ |
= |
ˆ |
= |
ˆ |
= |
(170,190+1,1577 |
|
40) |
|
0,90=195,2. |
||||||
y40 |
|
y44 |
|
y01.04.12 |
|
|
|
|
||||||||
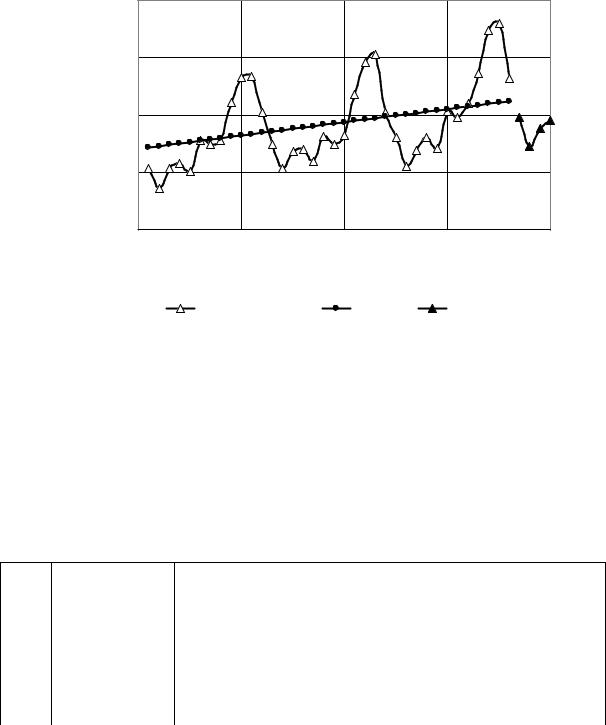
10. Строим графики исходного ряда, тренда и прогноза на следующие четыре месяца, рис. 9.11.
136
электроэнергии |
300 |
|
|
|
|
|
250 |
|
|
|
|
||
200 |
|
|
|
|
||
|
|
|
|
|
||
Потребление |
150 |
|
|
|
|
|
100 |
|
|
|
|
||
0 |
10 |
20 |
30 |
40 |
||
|
||||||
|
|
|
Месяцы |
|
|
|
|
|
Исходныйряд |
Тренд |
Порогноз |
|
Рис. 9.11 – Прогноз при наличии сезонной составляющей в мультипликативной модели
Мультипликативная модель лучше:
Eотн. ошиб. мульт. < Eотн. ошиб. аддит..
Таблица 9.11
Сопоставление прогнозных значений, найденных разными методами
Порядковый номер
Месяц
Прогноз с помощью скользящей средней |
Прогноз с помощью экспоненциальног о сглаживания |
Прогноз по кривой роста |
Прогноз по аддитивной модели |
Прогноз по мульти пликативной модели |
|
|
|
|
|
37 |
Январь 2012 |
196,722 |
239,97 |
228,313 |
201,0 |
198,1 |
38 |
Февраль 2012 |
|
|
230,250 |
178,0 |
172,3 |
39 |
Март 2012 |
|
|
232,187 |
192,5 |
188,4 |
40 |
Апрель 2012 |
|
|
234,124 |
198,8 |
195,2 |
Вывод. Для составления прогноза надо учитывать наличие сезонных колебаний.
137
9.5 Адаптивные модели временных рядов Задание 4
Спрос на джинсы в магазине «Спортмастер» (апрель 2009 – март 2012 г.), шт./мес. представлено в табл. 9.12.
Построить адаптивную модель Брауна с линейной тенденцией и сделать прогноз продаж в апреле, мае, июне 2012 года.
Таблица 9.12
Количество проданных джинсов: апрель 2009 – март 2012 г
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
yt |
149 |
136 |
153 |
158 |
151 |
178 |
174 |
180 |
201 |
222 |
220 |
220 |
t |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
yt |
220 |
215 |
216 |
230 |
231 |
235 |
251 |
252 |
254 |
280 |
253 |
256 |
t |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
yt |
260 |
263 |
268 |
270 |
278 |
280 |
282 |
260 |
262 |
274 |
279,5 |
281 |
Решение. 1. По первым пяти точкам временного ряда оцениваем с помощью МНК значения a0(0) и a1(0) параметров линейной модели
|
|
|
|
ˆ |
(t ) |
= |
ˆ |
+ ˆ |
(9.28) |
|
|
ˆ |
(t ) |
= |
y0 |
|
a0(0) |
a1(0)t . |
|||
Получим |
|
+ |
2,5t . |
|
|
|||||
y0 |
|
141,6 |
|
|
|
|||||
2.Находим прогноз на первый шаг при t =1 yˆ1 = aˆ0(0) + aˆ1(0) 1 =141,6 + 2,5 1 =144,1.
3.Находим величину отклонения e1 = y1 − yˆ1 =149 −144,1 = 4,9 .
Дальнейшие расчёты оформляем в табл. 9.13. Средняя относительная ошибка прогноза Еотн. = 4,0 .
Среднее et2 =11,5.
4. Корректируем параметры модели aˆ0(1) и aˆ1(1) по формулам
aˆ0(t) = aˆ0(t −1) + aˆ1(t−1) +(1− β2 )e(t ),
aˆ1(t) = aˆ1(t) +(1− β)2 e(t ).
Вычисления проводим при α = 0,1, β =1−α = 0,9.
aˆ0(1) = aˆ0(0) + aˆ1(0) +(1− β2 )e(1) =141,6+2,5+(1−0,72 ) 4,9=146,6 , aˆ1(0) = aˆ1(0) +(1− β )2 e(1) = 2,5+(1−0,7)2 4,9=2,9 .
(9.29)
(9.30)
Получим
yˆ1 (τ ) =146,6 + 2,9τ .
138
