Metodichka_lab_Ekonometria

Этот коэффициент также необходимо проверить на значимость с помощью F -критерия Фишера

сравнивается с табличным Fтабл. (α,ν1,ν2 )= Fтабл. (0,05;m;n − m −1). Если Fрасч. > Fтабл. , то проверяемый множественный коэффициент корреляции

значим.

Расчет по формуле (4.7), скорректированных множественных коэффициентов корреляции и их проверка по F-критерию Фишера, позволяет последовательно отбирать факторы, оказывающие существенное влияние на результативный признак. При этом первым в уравнение включается фактор, наиболее тесно коррелирующий с Y , вторым – тот фактор, который в пареспервымизотобранныхдаетмаксимальноезначение R ит. д.

На каждом шаге получают новое значение множественного коэффициента корреляции Ryx j , бóльшее чем на предыдущем. Тем самым

определяется вклад каждого отобранного фактора в объясненную дисперсию Y .

Второй метод пошаговой регрессии основан на последовательном исключении факторов с помощью t-критерия Стьюдента. Она заключается в том, что после построения уравнения регрессии и оценки значимости всех коэффициентов регрессии из модели исключается тот фактор, коэффициент при котором незначим и имеет наименьшее значение t-критерия. После этого получают новое уравнение множественной регрессии и снова производят оценку значимости всех оставшихся коэффициентов. Если среди них окажутся незначимые, то опять исключают фактор с наименьшим значением t-критерия. Процесс исключения факторов останавливается на том шаге, когда все регрессионные коэффициенты становятся значимыми.

Расчётный t-критерий Стьюдента определяют по формуле

где

49

Замечание. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов в 6–7 раз меньше объема совокупности, по которой строится регрессия.

После отбора факторов по одной из указанных схем и построения множественной регрессионной модели осуществляется статистическая проверка этой модели по методике, аналогичной рассмотренной для статистического анализа однофакторной регрессионной модели.

Проверку качества уравнения регрессии осуществляют с помощью коэффициента детерминации, множественной корреляции и средней относительной ошибки аппроксимации.

Коэффициент детерминации можно рассчитать по формуле

Статистическая значимость коэффициента детерминации проверяется аналогично – путём сравнения Fфакт. и Fтабл. , где

Fфакт. > Fтабл. , то принимается гипотеза о том, что R2 статистически значим.

Для проверки значимости коэффициента множественной корреляции вычисляют t-критерий Стьюдента

50

критерия Стьюдента с n − m −1 степенями свободы и уровнем значимости

α .

Если tрасч. > tтабл. = tα; n-m-1, то коэффициент множественной

корреляции между регрессантом и регрессорами значим.

Для определения стандартных ошибок и нахождения доверительных интервалов оценок параметров aˆ j используется дисперсионно-

(4.15)

Значимость коэффициентов уравнения регрессии проверяется с помощью сравнения фактических и табличных значений t-критерия Стьюдента:

статистически значимым. Доверительные интервалы для параметров модели имеют вид

Средняя относительная ошибка аппроксимации находится по формуле

4.1.2 Организация данных и расчетов на листе MS Excel

Рассмотрим пример выполнения лабораторной работы 4 (задание 4.1). Для выполнения задания 1 нужно создать новую рабочую книгу MS Excel, в ячейки которой ввести исходные данные задачи (рис. 4.1):

51

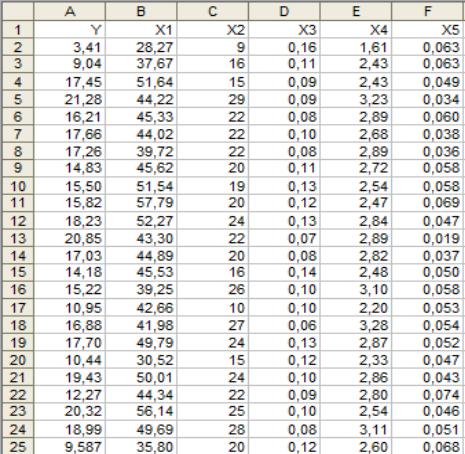
значения показателей производительности труда – Y (млн грн/г.), фондоемкости X1 (тыс. грн), стажа работы X 2 (года), текучести кадров

X3 (в долях), средней заработной платы X 4 (тыс. грн) и потерь рабочего времени X5 (в долях).

Для построения модели применим алгоритм пошаговой регрессии. На первом шаге построим пятифакторную линейную модель

5

yˆ = aˆ0 + ∑aˆ j x j . Для этого во вкладке «Сервис» выберем пункт «Анализ

j =1

данных», в котором в свою очередь выберем функцию «Регрессия». После этого появится диалоговое окно (рис. 4.2), в котором нужно ввести ссылки на входные интервалы, выделяя их последовательно курсором. Следует отметить, что ссылка на значения факторов-аргументов должна быть неразрывной. Также нужно установить другие необходимые параметры задачи (например, «Вывод остатков») и нажать «ОК». После этого появится отчет, как представлено на рис. 4.3.

Рис. 4.1 – Исходные данные лабораторной работы 4

52

Из полученного отчета (рис. 4.3) выпишем уравнение регрессии

Rн2 = 0,981).

Значимость уравнения множественной регрессии в целом определяется с помощью статистического F-критерия Фишера (4.8). В отчете функции «Регрессия» (раздел «Дисперсионный анализ») в ячейке L13 хранится значение Fфакт., которое можно использовать для

проведения F-теста. Можно использовать второй подход и проверить выполнение неравенства P(F < Fфакт.) ≤α (где α = 0,05 заданный уровень

(9,10 10−16 < 0,05), то пятифакторное уравнение регрессии значимо с надёжностью не менее 95 %.

Проверку значимости коэффициентов полученного уравнения можно выполнить двумя способами. Первый – по критерию Стьюдента (формулы 2.9 – 2.12). Второй – проверить выполнение неравенства P(t < t j,факт.) ≤α ,

«Регрессия» (ячейки L19 : L23). Заметим, что свободный член a0 обычно

не проверяется на статистическую значимость. В столбце «P-значение» (рис. 4.3) только одно значение (ячейка L21) для переменной X3 больше

заданного уровня значимости α = 0,05. Следовательно оценка

выпишем уравнение регрессии yˆ = −1,07 +0,3x1 +0,17x2 +2,93x4 −157,89x5

( R2 = 0,984 , Rн2 = 0,980 ). Анализируя значения P(t <t j,факт. ) в столбце «P- значение» отчета функции «Регрессия» (ячейки K 47 : K50, рис. 4.4) делаем вывод, что все они удовлетворяют условию P(t <t j,факт. ) ≤α , j =1,2,4,5 . Следовательно все коэффициенты модели статистически значимы.

Используя данные отчета функции «Регрессия» (раздел «Вывод остатков») рассчитаем среднюю относительную ошибку аппроксимации четырехфакторной модели. Для этого в ячейки J 57 : J80 (рис. 4.5) скопируем значения результативного признака Y , в ячейки K57 : K81 введем формулы как указано в табл. 4.2.

54

выполняется условие 2,68 % < 7 % , то качество модели хорошее. По

значению коэффициента детерминации R2 = 0,984 делаем вывод, что полученное уравнение регрессии объясняет колебания результативного признака Y на 98,4 % , остальные 1,6 % приходятся на факторы,

неучтенные в модели. Следовательно, построенную модель можно использовать для дальнейшего экономического анализа и прогноза.

При увеличении фондоемкости на 1 тыс. грн (при условии неизменности остальных факторов) производительность труда увеличивается в среднем на 0,3 млн грн/г. При увеличении стажа работы на 1 год (при условии неизменности остальных факторов) производительность труда увеличивается в среднем на 0,17 млн грн/г. При увеличении средней заработной платы на 1 тыс. грн (при условии неизменности остальных факторов) производительность труда увеличивается в среднем на 2,93 млн грн/г. При увеличении потерь рабочего времени на 1 % (при условии, неизменности остальных факторов) производительность труда уменьшается в среднем на 1,57 млн грн/г.

Для того, чтобы сделать окончательный вывод о возможности использования модели в экономическом анализе необходимо проверить для построенной модели выполнение условий Гаусса–Маркова (наличие мультиколлинеарности между факторами-аргументами, гетероскедастичности и автокорреляции возмущений).

4.2 Проверка предпосылки отсутствия мультиколлинеарности между факторами-аргументами. Методы устранения мультиколлинеарности (задание 4.2)

4.2.1 Теоретические замечания

Одним из условий МНК при оценке параметров регрессионной модели является предположение о линейной независимости объясняющих

56

переменных. Для экономических показателей это условие выполняется не всегда. Тогда говорят о наличии мультиколлинеарности между факторамиаргументами модели. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.

Основными последствиями мультиколлинеарности являются:

−снижение точности оцениваемых параметров;

−оценки параметров модели не являются состоятельными (небольшое увеличение количества наблюдений приводит к значительным изменениям в оценках параметров);

−экономическая интерпретация параметров уравнения регрессии затруднена, так как некоторые из его коэффициентов могут иметь неправильные, с точки зрения экономической теории, знаки и неоправданно большиезначения.

Признаки мультиколлинеарности:

−наличие высоких значений парных коэффициентов корреляции rxi x j ≥ 0,8 ;

− определитель матрицы X ′X близок к нулю;

−существенноеприближениекоэффициентамножественнойкорреляции

кединице;

−наличие малых значений оценок параметров модели при высоком

уровнекоэффициентадетерминации R2 иF-критерияФишера;

−существенное изменение оценок параметров модели при дополнительном введении в нее новой объясняющей переменной;

−резкое изменение значений параметров при увеличении числа наблюдений.

Алгоритм Фаррара–Глобера позволяет статистически подтверждать или опровергать гипотезу о наличии тесной корреляционной связи между аргументами Xi модели. Основу алгоритма составляют три

статистических критерия (данные критерии детально описаны в лабораторной работе 2), с помощью которых проверяется мультиколлинеарность.

На первом шаге с помощью критерия χ2 Пирсона определяют наличие мультиколлинеарности во всем массиве данных X1, X 2 ,..., X m .

На втором шаге с помощью F-критерия Фишера определяют для каждого аргумента k =1,m существует, или нет мультиколлинеарность

между ним и другими факторами.

На третьем шаге с помощью t-критерия Стьюдента определяют наибольшую связь между выделенным Xk на втором шаге и всеми

остальными факторами поочередно.

При выявлении мультиколлинеарности нужно предпринять меры для ее устранения. Для этого можно использовать следующие методы.

57

Исключить из модели одну из переменных мультиколлинеарной пары. Но такой метод часто противоречит действительности экономических связей между факторами и к нему надо относиться осторожно.

Можно преобразовать объясняющие переменные и вместо их абсолютных значений взять их отклонения от среднего значения (xij − xj ).

стандартизировать объясняющие переменные.

Если вышеуказанные приёмы не помогают исключить мультиколлинеарность, то надо поменять спецификацию модели (взять не линейную, а другой вид модели).

Если и эти действия не привели к достижению цели, то есть мы не избавились от мультиколлинеарности, то оценки параметров следует рассчитывать с помощью другого метода, например, метода главных компонент.

4.2.2 Организация данных и расчетов на листе MS Excel

Рассмотрим пример выполнения лабораторной работы 4 (задание 4.2).

Проверим наличие мультиколлинеарности между четырьмя факторами-аргументами, влияние, которых на результативный фактор изучалось в работе первой части лабораторной работы 4.

Для проверки мультиколлинеарности в массиве данных выполним расчеты на листе MS Excel (рис. 4.6) по формулам (2.1), (2.3), (2.4), (2.6), (2.7) лабораторной работы 1, а также найдем табличные значения соответствующих критериев (в табл. 2.1 описаны функции MS Excel для выполнения расчетов).

4.2.3 Выводы по результатам проверки наличия мультиколлинеарности между факторами-аргументами

На основании проведенных расчетов сделаем следующие выводы.

1.Так как χфакт2 . > χтабл2 . (44,126 >18,307) то в массиве переменных X1, X 2 , X 4 , X5 существует мультиколлинеарность.

2.Так как условие Fфакт. > Fтабл. ( Fтабл. = 2,895 ) выполняется для статистик F2 и F4 то делаем вывод (с достоверностью 95 %) о

статистической значимости коэффициентов множественной корреляции показателей X 2 , X 4 и тесной линейной зависимости каждого из факторов с

остальными.

58