Metodichka_lab_Ekonometria

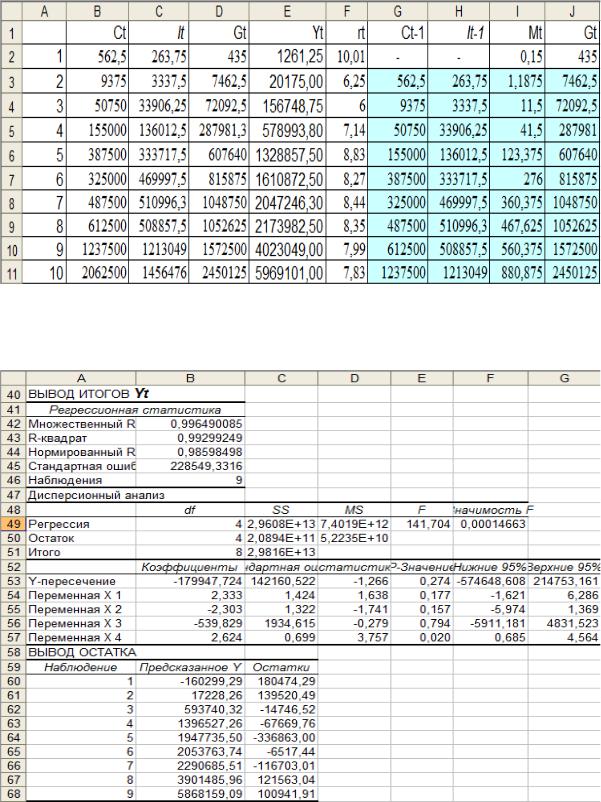
Рис. 8.1 – Организация данных для оценки параметров структурной формы модели лабораторной работы 8

Рис. 8.2 – Результаты оценки параметров третьего уравнения структурной формы модели (8.9)

109

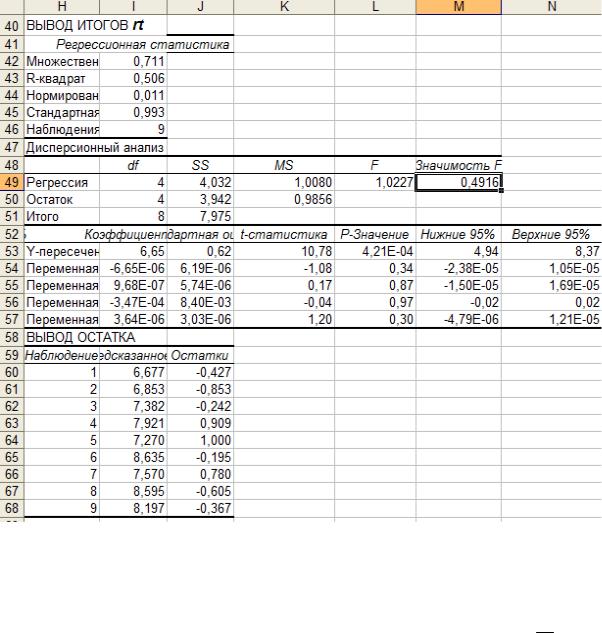
Рис. 8.3 – Результаты оценки параметров четвертого уравнения структурной формы модели (8.9)

Применяя к каждому из полученных уравнений в отдельности 1– МНК определим оценки структурных параметров aˆi , bi1, bi2 , ,i =1,3 (рис.

8.4– 8.5).

8.4Результаты оценивания параметров уравнений двухшаговым

МНК

В результате получим структурную форму модели

Yt = Ct + It + Gt .

110

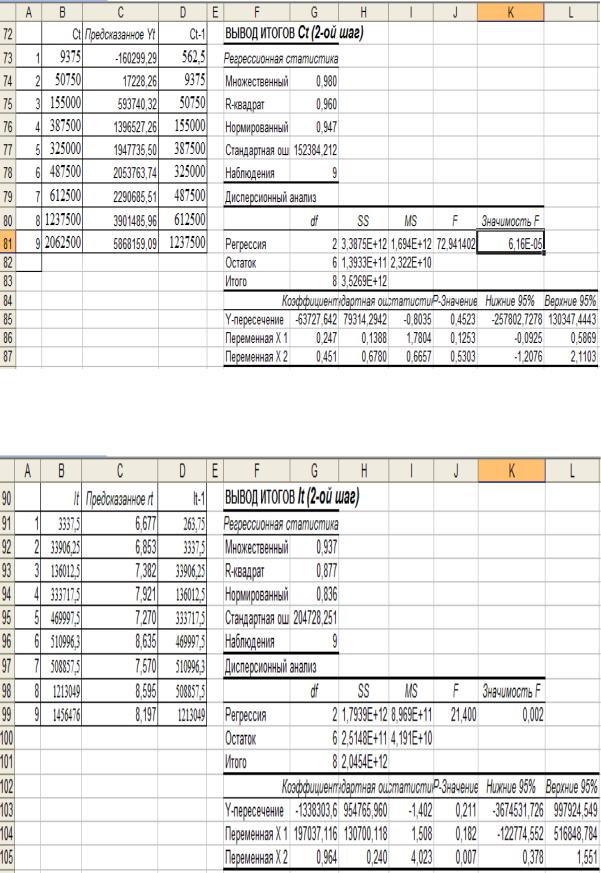
Рис. 8.3 – Результаты оценки параметров первого уравнения приведенной формы модели (8.10)

Рис. 8.4 – Результаты оценки параметров второго уравнения приведенной формы модели (8.10)

111

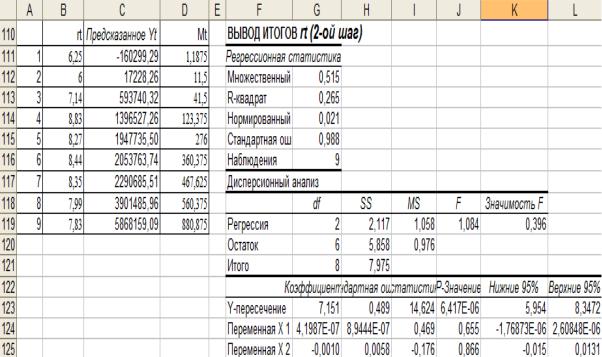
Рис. 8.5 – Результаты оценки параметров третьего уравнения приведенной формы модели (8.10)

Анализируя данные отчетов о значимости коэффициентов и уравнений модели (8.11) в целом (рис. 8.3 – 8.5) делаем вывод, что первое

ивторое уравнения моделей значимы (при заданном уровне значимости

α= 0,05) в целом, но среди коэффициентов значимый только коэффициент

b22 = 0,964 во втором уравнении при переменной It −1 . В первом уравнении

причиной данного факта скорее всего является мультиколлинеарность между объясняющими факторами, так как коэффициент парной корреляции между ними близок к единице: r(Yt ,Ct −1) = 0,98 . Третье

уравнение модели в целом и его коэффициенты незначимы (при заданном уровне значимости α = 0,05). Поэтому использовать данную модель для дальнейшего экономического анализа и прогноза нежелательно. Следует дать рекомендации исследователю увеличить количество данных наблюдений или поменять спецификацию модели.

2. Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на единицу (из модели будет исключена переменная Gt ). Число эндогенных переменных модели

также снизится на единицу – переменная Yt станет экзогенной. В правых

частях функций потребления и денежного рынка (первое и третье уравнения структурной формы модели (8.8)) будут только предопределенные переменные. Второе уравнение структурной формы модели (8.8) – функция инвестиций определяет зависимость эндогенной переменной It от эндогенной переменной rt (которая зависит только от

112

предопределенных переменных) и предопределенной переменной It −1 . Таким образом, получим рекурсивную систему

Параметры системы (8.12) можно оценивать 1–МНК и нет необходимости исследования системы на идентификацию.

8.5 Вопросы для самоподготовки к лабораторной работе 8

1.Система независимых регрессионных уравнений. Ее формальная запись. Метод ее решения.

2.Система рекурсивных регрессионных уравнений. Ее формальная запись. Метод ее решения.

3.Система одновременных уравнений. Ее формальная запись.

4.Вид структурной формы модели одновременных регрессионных уравнений. Эндогенные и экзогенные переменные.

5.Приведенная форма модели одновременных регрессионных уравнений. Причины, вызывающие необходимость построения приведенной формы модели.

6.Примеры практической постановки задач систем одновременных уравнений: первая модель спроса и предложения; вторая модель – кейнсианская модель спроса и предложения. Эндогенные лаговые переменные.

7.Идентификация переменных. Предопределенные переменные системы одновременных уравнений.

8.Классы структурной модели относительно идентифицируемости регрессионных уравнений.

9.Необходимое и достаточное условие идентифицируемости уравнений структурной формы модели. Показать на примере.

10.Алгоритм косвенного метода решения систем одновременных уравнений.

11.Алгоритм двухшагового метода наименьших квадратов для решения систем одновременных регрессионных уравнений.

113

Раздел 9 Эконометрические модели динамики

9.1 Теоретические замечания Определение. Временной ряд – это набор чисел, привязанных к

последовательным, обычно равноотстоящим моментам времени. Временной ряд – это совокупность значений какого–либо показателя за несколько последовательных моментов или периодов.

Числа, составляющие временной ряд и полученные в результате наблюдения за ходом какого–либо процесса, называются уровнями (или

элементами) ряда.

Длиной временного ряда называют количество входящих в него уровней.

Временной ряд обычно обозначают Y (t ) или yt , где t =1,n .

В моделях временного ряда выделяют две основные составляющие:

−детерминированную (систематическую);

−случайную.

Определение. Детерминированной составляющей временного ряда y1, y2,..., yn называют числовую последовательность, элементы которой

вычисляются по определённому правилу как функция времени t . Исключив детерминированную составляющую из данных, получим

колеблющийся вокруг нуля ряд, который может представлять собой случайные скачки или плавное колебательное движение, так называемую

остаточную компоненту.

Детерминированная составляющая может содержать следующие структурные компоненты: тренд; сезонную; циклическую.

В общем случае каждый уровень временного ряда можно представить как функцию четырёх компонент: Q(t ), S (t ), Z (t), ε (t ),

отражающих закономерность и случайность развития,

где Q(t ) – тренд (долговременная тенденция) развития; S (t ) – сезонная компонента;

Z (t) – циклическая компонента; ε (t ) – остаточная компонента.

Определение. Тренд, или тенденция Q(t ), представляет собой

устойчивую закономерность, наблюдаемую в течение длительного периода времени. Он описывается с помощью некоторой неслучайной функции Q(t ),

где t – время.

Определение. Сезонная компонента S (t )описывает регулярные

колебания, которые носят заранее известный периодический или близкий к нему характер и заканчиваются в течение периода наблюдения (года, квартала, месяца).

114

Определение. Циклическая компонента Z (t ) – неслучайная

функция, описывающая длительные периоды (более одного года) относительного подъема и спада, состоящая из циклов переменной длительности и амплитуды (вековые циклы, экономические циклы Кондратьева и так далее).

Определение. Случайная компонента ε (t ) – это составная часть

временного ряда, оставшаяся после выделения систематических компонент. Она отражает воздействие многочисленных факторов случайного характера.

В зависимости от вида связи между перечисленными компонентами

Не всегда предполагается участие всех четырёх компонент, но случайная составляющая рассматривается всегда.

Основной целью исследования временных рядов является составление прогноза.

Предварительный анализ временных рядов и экономических показателей заключается в выявлении аномальных значений уровней ряда, которые не соответствуют реальным возможностям рассматриваемой экономической системы, а также определению наличия тренда.

Наиболее распространённым приемом для устранения аномальных значений показателя является сглаживание временного ряда. При этом производится замена фактических уровней временного ряда расчётными, что способствует более чёткому проявлению тенденции.

Существующие методы сглаживания делятся на две группы. Аналитические методы. Для сглаживания используется кривая,

проведенная относительно фактических значений ряда так, чтобы она отражала тенденцию, присущую ряду и одновременно освобождала его от мелких незначительных колебаний. Такие кривые называются кривыми роста и применяются, главным образом, для прогнозирования экономических показателей.

Методы механического сглаживания. Сглаживается каждый отдельный уровень ряда с использованием фактических значений соседних с ним уровней.

Для сглаживания временных рядов используются разные методы.

115

Метод простой скользящей средней состоит в следующем.

Определяется количество наблюдений m , входящих в интервал сглаживания. При этом, если необходимо сгладить мелкие беспорядочные колебания, интервал сглаживания берут по возможности большим. Если нужно сохранить более мелкие волны, но освободиться от периодических, повторяющихся колебаний, то интервал сглаживания уменьшают. Если m нечётное число, то сглаживание производится по формуле

сглаживаемого.

При применении этой формулы несглаженными остаются первые и последние p уровней ряда. Чтобы сгладить последние уровни ряда

используют следующую формулу скользящей средней

Наиболее часто выбирают α = 0,3. α −параметр сглаживания, β =1−α имеет название коэффициента дисконтирования или фактора затухания.

При использовании экспоненциального сглаживания возникает проблема выбора F0 и α . Формула также может изменятся. В

компьютерной программе Excel, экспоненциальное сглаживание

используется

При использовании компьютерных программ необходимо просматривать формулы, которые в них используются.

Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры

116

к изменению условий. При оценке параметров адаптивных моделей наблюдениям присваиваются различные веса в зависимости от того, насколько сильным признаётся их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность. К адаптивным моделям относится метод Брауна. Метод Брауна представляет процесс развития как линейную тенденцию с постоянно изменяющимися параметрами. Метод Брауна применяется при прогнозировании макро– и микроэкономических параметров экономических систем, в том числе торговых. Он позволяет получить хороший прогноз тренда для коротких рядов с постоянным трендом, достаточно часто используется для прогноза продаж различных пищевых продуктов.

Под сезонными колебаниями понимают регулярные, периодические внутригодовые, внутриквартальные, внутримесячные подъёмы и спады производства, деловой активности, грузооборота, товарооборота и прочего, в основном связанного со сменой времён года.

Определение. Временной ряд, в котором наблюдаются тренд и сезонные колебания, называется тренд-сезонным временным рядом.

Сезонность отрицательно влияет на экономические процессы, поэтому её необходимо уметь измерять, анализировать и учитывать в строящихся моделях.

Для исследования и прогнозирования тренд-сезонных экономических процессов независимо от причин, порождающих сезонные колебания, необходимо решать следующие задачи:

−определять наличие во временном ряде тренда;

−выявлять присутствие во временном ряде сезонных колебаний;

−осуществлять фильтрацию временного ряда, то есть разделять ряд на составляющие его компоненты: тренд, сезонную и случайную компоненты;

−анализировать динамку сезонной волны, то есть выявлять изменяется ли со временем ее амплитуда, и происходит ли перемещение точек экстремума сезонной волны;

−составлять прогноз тренд-сезонного экономического процесса. Порядок решения перечисленных задач, их состав, может изменяться

взависимости от цели исследования, методов решения, используемых пакетов прикладных программ и других факторов.

Решение задачи определения наличия во временном ряде тренда можно осуществить или визуально, путём нанесения на график соответствующего исходноговременногоряда, илианалитическимиметодами.

При использовании визуального метода необходимо последовательно нанести на график все уровни тренд-сезонного временного ряда либо для каждого года строить отдельную кривую, причём кривые, соответствующие каждому году, будут располагаться друг над другом.

117