
Лекция 19 и 20
.pdf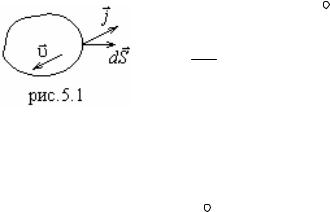
Глава 5. Постоянный электрический ток.
§ 5.1 Вектор плотности тока. Закон Ома.
Движение заряженных частиц в проводниках под действием приложенного электрического поля назвали электрическим током.
Подвижными заряженными частицами в металлах являются электроны. Носители тока в полупроводниках - также электроны; в электролитах – ионы, в плазме – ионы и электроны.
Основной характеристикой тока является плотность тока j:
j n e , (5.1)
где - средняя скорость электрона. Видно, что вектор j направлен вдоль скорости движения положительных зарядов.
Через площадку dS за единицу времени протекает количество электронов (количество электричества):
dI j dS . |
|
|
|
|
(5.2) |
||
Тогда I j dS - сила тока, проходящего через площадку |
S . Единицей |
||||||
S |
|
|
|
|
|
||
измерения плотности тока j является |
Кл |
|
А |
, силы тока I - А (ампер). |
|||
|
м2 |
||||||
|
м2 с |
|
|
|
|
||
Рассмотрим произвольную замкнутую |
поверхность |
S (рис.5.1) и |
|||||
найдем поток вектора j сквозь эту поверхность: |
|
|
|
|
|||
|
|
|
|
|
dQ |
|
|
|
I j dS |
|
|
, |
(5.3) |
||
|
|
||||||
|
S |
|
|
dt |
|
||
|
|
|
|
|
|
||
где dQ - изменение заряда в единицу времени. dt
Q dV .
V
Знак “-” показывает, что если число положительных зарядов в объеме
уменьшается, то поток j направлен из объема V наружу. |
|
|||||
|
|
d |
|
|
|
|
j dS |
dV ; |
|
||||
|
|
|
||||
S |
V |
dt |
|
|
|
|
|
d |
|
||||
|
|
|
|
|||
|
div j |
|
. |
(5.4) |
||
|
|
|||||
dt
Уравнение (5.4) представляет собой уравнение непрерывности, выражающее закон сохранения заряда в объеме.
Сравним его с теоремой Гаусса в дифференциальной форме:
|
ρ |
|
divE |
|
; |
|
||
|
0 |
|
Смысл уравнения в том, что источниками E являются заряды . Значит, из уравнения непрерывности следует, что источником тока является

временное изменение заряда, токовые силовые линии начинаются там, где
d 0. dt
Для постоянного тока j f t , |
f t , то есть |
d |
0, |
div j 0: |
|
||||
|
|
dt |
|
|
токовые линии всегда замкнуты для постоянного тока.
Выясним условия, при которых может существовать постоянный ток. Для этого нужны сторонние источники, создающие направленное
движение зарядов ( 0). Связь j с E (напряженность стороннего поля)
предполагается линейной: |
|
|
j σ E |
- |
(5.5) |
Здесь - коэффициент электропроводности; |
См сименс . Эта |
|
формула верна в точке проводника, где j и E постоянны, то есть имеет локальный характер, и носит название закона Ома в дифференциальной форме. Открыт Омом в 1827 г. Кавендиш установил экспериментально пропорциональность тока и напряжения еще в 1770 г., но никому об этом не сообщил.
Исследуем выражение (5.5) и найдем следствия из него. С учетом
(5.1) имеем:
|
|
|
|
|
|
j |
E |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оценим величину . |
|
n e |
n e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
||||||
|
29 |
|
3 |
|
I 1 А, |
S 1мм |
2 |
10 |
6 |
м |
2 |
; то 10 |
4 |
||||||||
Для Cu: n 10 |
|
м |
|
, и если |
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
с |
||
Скорость теплового движения при T 300 K : T |
10 |
5 |
|
; тогда T . |
|||||||||||||||||
|
|
с |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как E const, то const , т.е. движение электронов является равномерным, а должно быть равноускоренным, потому что происходит под действием силы. Чтобы объяснить это противоречие, запишем уравнение движения электронов:
|
|
|
|
|
(5.6) |
m e E , |
||
где второе слагаемое учитывает столкновение электронов с решеткой в виде “эффективной силы трения“. Решение уравнения (5.6) имеет вид:
|
|
|
|
t |
|
|
|||||
Ae |
|
m |
B; |
||
B найдем подстановкой решения в уравнение; A - из начальных условий: t 0, 0:
|
eE |
|
eE |
||
B |
|
, |
A |
|
. |
|
|
||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
||||
Таким образом: |
eE |
1 e τ |
|
, |
(5.7) |
|||
|
|
|
|
|||||
|
||||||||
|
|
|
|
|
|
|
|
|

где параметр m называется временем релаксации.
При t скорость электронов становится постоянной: |
|
||||||||||
|
|
eE |
|
|
|
|
|
||||
|
|
|
|
|
|
|
E. |
|
|
||
|
|
|
|
|
|
||||||
Тогда: |
|
n e |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
n e2 |
|
n e2 |
|
|
|
|||||
|
|
|
|
|
|
|
. |
- |
(5.8) |
||
|
|
m |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
Эта зависимость электропроводности от плотности электронов называется
формулой Друде.
Оценим время релаксации.
|
|
|
|
eE |
|
|
eE 10 |
19 10 |
1 |
16 |
кг |
||||||
Для Ag: T 300 |
|
K; |
|
|
; |
|
|
|
|
|
|
|
10 |
|
|
; |
|
|
|
|
|
|
10 4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
с |
||||||
|
|
|
|
|
|
m |
|
10 30 |
10 14 с. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
10 16 |
|
|
|
|
|
|
||||
Ясно, что установление постоянного значения после включения E происходит очень быстро.
Куда уходит энергия, получаемая электронами в процессе разгона? На преодоление сил ”трения”, то есть на столкновения электронов с
решеткой, что приводит к ее нагреванию. При движении |
заряда |
||||
|
|
|
|
||
совершается работа eE dt. В единице объема выделится энергия: |
|||||
|
|
|
|
(5.9) |
|
dW eE dt n j E dt |
|||||
Значит, за единицу времени в единице объема выделится энергия: |
|
||||
P j E. |
|
|
(5.10) |
||
Данная величина носит название тепловой мощности. Иначе: |
|
||||
P |
dA |
|
dW |
. |
(5.11) |
|
|
||||
|
dt |
dt |
|
||
Закон Джоуля (1841г.), Ленца (1842 г.) в дифференциальной форме, записанный выше, верен в локальной точке проводника.
Интегральный вид этого закона можно вывести, зная количество тепла, выделившегося в проводнике объема dV за время t. Введем величину удельного сопротивления:
|
1 |
. |
(5.12) |
|
|
||
|
σ |
|
|
Тогда, используя (5.9), запишем: |
|
||
dW j E t dV j2 t dV . |
(5.13) |
||
Для линейного проводника dV S dl, где S - площадь сечения, dl - элемент длины, I j S. С учетом этого выражение (5.13) примет следующий вид:
dW I2 t S dl;
S2

W t |
I |
2 |
S dl t I 2 |
|
dl |
I2R t; |
||
|
||||||||
S |
2 |
|
||||||
|
|
|
W I2R t, |
|
S |
|||
|
dl |
|
|
(5.14) |
||||
где величина R |
|
|
характеризует |
сопротивление проводника. |
||||
S |
|
|||||||
|
|
|
|
|
|
|||
Подставляя выражение (5.14) в (5.11), получаем окончательно выражение для тепловой мощности:
P I2R. |
(5.11’) |
Единицей измерения мощности является ватт 1 Вт 1 А2 1 Ом.
В основе всех приведенных выше формул лежит закон Ома. Область применимости этого закона связана с линейной зависимостью j~ E, т.е. E должно быть достаточно малым, чтобы ограничиться первым членом ряда:
E j j n e .
σ
Здесь единственная величина, которая может быть ограничена, это :
T .
|
|
|
|
|
|
T ~ |
kT |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тепловая скорость электронов. Тогда E n e T . |
|
|
|
|
|
|
||||||||||||
|
|
5 |
м |
|
|
|
|
7 |
В |
|
7 |
|
8 |
|
В |
|||
T |
10 |
|
|
, |
T 300 K, |
n e T ~10 |
|
|
, |
E (10 |
|
10 |
|
) |
|
. |
||
|
|
|
|
|
|
|
||||||||||||
|
|
|
с |
|
|
|
|
|
м |
|
|
|
|
|
м |
|||
Только начиная с таких полей могут проявляться нелинейные эффекты в законе Ома при прохождении тока в металлах. Технически допустимые значения E можно определить по максимальному значению допустимой плотности тока в металлических проводах. Так, для меди :
jmax ~10 |
3 А |
|
10 |
7 |
А |
; |
|
|
(5.15) |
|||
|
см2 |
|
|
м2 |
|
|
||||||
|
|
|
В |
|
|
В |
|
|||||
|
|
|
2 |
|
|
|
|
|
||||
Emax ~ (1 0,1) 10 |
|
|
|
~ (0,1 1) |
|
. |
(5.16) |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
см |
|
|
|
м |
|
||
Таким образом, технически используемые величины E в 109 108 раз меньше тех, которые ограничивают область применения в законе Ома.
В плазме закон Ома не соблюдается, так как при низких давлениях величина велика T (почти нет столкновений): {n ~ 1018 1021 м 3 при гораздо большем токе, чем в металлах}.
§ 5.2. Электродвижущая сила. Правила Кирхгофа.
Закон Ома для замкнутого проводника или для электрической цепи можно вывести, используя выражения (5.5), (5.12). Возьмем замкнутый проводник, элемент длины которого dl || j. Тогда:

 E dl
E dl  ρ jdl ;
ρ jdl ;
L |
L |
|
|
|
Используем то, что сила тока, или просто ток, |
I j S. Тогда: |
|
||
|
|
dl |
|
|
ρ jdl I |
. |
|
||
|
|
|||
L |
L |
S |
|
|
|
|
|
||
Таким образом: |
|
|
|
|
E dl IR ; |
(5.17) |
|||
L |
|
|
I R. |
|
E dl |
или |
|
|
|
L |
|
|
|
|
Это закон Ома для замкнутого проводника. Здесь R - полное сопротивление всей цепи. Так как для электростатического поля
 E dl 0 то для того, чтобы ЭДС было отлично от нуля 0, нужны
E dl 0 то для того, чтобы ЭДС было отлично от нуля 0, нужны
L
сторонние непотенциальные источники электрического поля.
Из (5.17) следует определение :
ЭДС – это работа сторонних сил по перемещению единичного положительного заряда вдоль замкнутого проводника.
Если участок цепи не содержит источника, то закон Ома принимает вид:
1 2 |
I R, |
(5.18) |
где 1 2 - разность потенциалов на этом участке цепи. |
||
Применим закон Ома для |
изучения |
последовательного и |
параллельного соединения проводников.
1. Случай последовательного соединения проводников (рис.5.2). Используя (5.18), запишем для каждого проводника:
|
R1 |
|
R2 |
I |
|
|
IR ; |
|
|
|
|
3 |
1 |
2 |
1 |
|
|
|
|
||||
1 |
|
|
2 |
2 3 IR2; |
|||
|
рис.5.2 |
|
3 1 |
IR1 IR2 IR . |
|||
Таким образом, для последовательного сопротивления проводников:
R Ri . (5.19)
2. Случай параллельного соединения проводников (рис.5.3). Для точки А
можно записать:
R1
I I1 |
I2 |
; |
|
A |
|
|
|
B |
|
||||||||
I |
|
|
|
|
||||
|
|
|
|
|
|
R2 |
|
|
Тогда по (5.19): |
|
|
|
|
|
рис.5.3 |
||
|
|
|
|
|
|
|
|
|
|
A |
|
B |
I |
1 |
R ; |
I1 I2 A B |
|
1 |
|
1 |
|
|
|
A |
|
B |
|
|||
|
|
|
1 |
; |
|
|
|
|
|
|
. |
||||||||||
|
|
|
I |
|
R |
|
|
R |
|
|
|
R |
|
||||||||
A |
B |
2 |
2 |
R |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
Значит, при параллельном соединения проводников: |
|
|
R 1 |
Ri 1 . |
(5.20) |
|
i |
|
Рассмотрим разветвленную цепь проводов, в отдельных участках которой включены источники тока. Для такой цепи могут быть выведены два правила Кирхгофа. Сформулируем их.
1.Это правило выражает закон сохранения заряда (5.4) для постоянного тока. Используем его в точках разветвления проводов (в узле).
div j 0 |
|
div |
j dV j dS I1 I2 |
I3 |
0. |
|
|
|
V |
|
S |
|
|
|
|
Ik |
0 |
- |
|
(5.21) |
|
|
k |
|
|
|
|
Правило читается так:
Алгебраическая сумма всех токов, текущех к узлу и вытекающих из него, равна нулю.
Токи, текущие от узла, имеют знак “+”, токи, направленные к узлу, знак
“-”.
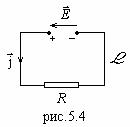
2. Выделим в цепи произвольный замкнутый контур. Применяя закон Ома (5.18) к каждому участку контура и суммируя, получим:
Ik Rk |
k |
- |
(5.22) |
k |
k |
|
|
Правило формулируется так:
Сумма падений напряжения на всех участках замкнутого контура равна сумме ЭДС, действующих в нем.
Знак перед любым слагаемым второго правила Кирхгофа, являющегося следствием закона Ома, определяется следующим образом: перед IR ставится “+”, если направление тока совпадает с направлением обхода контура; записывается с “+”, если направление вектора сторонней напряженности E совпадает с направлением обхода контура L
(рис.5.4.).
§ 5.3 Электропроводность металлов.
Рассмотрим электронную структуру изолированного атома, использовав модель Бора: ядро и вращающиеся вокруг него по соответствующим орбитам электроны. Каждая такая орбита характеризуется определенным значением энергии. Энергетическая структура атомов может быть представлена различными энергетическими уровнями, заселенными определенным количеством электронов (рис.5.5, а). Расстояние между уровнями убывает по мере роста номера

уровня (уровни не эквидистантны). Максимальное число электронов на уровне задано правилами квантования. На рис.5.5 это показано цифрами на уровнях Е1, Е2, и т.д.
Энергетическая структура всех изолированных атомов одного элемента одинакова. Если взять N атомов, то уровни Е1, Е2, Е3… будут N-кратно вырожденными, т.е. будут одинаково повторены N раз.
Сблизим N атомов так, чтобы они образовали кристалл. Расстояние между атомами в кристалле всегда несколько
меньше, чем размер внешних оболочек атома, т.е. валентные электронные оболочки перекрываются. Это означает, что на уровне Ei должно находиться большее, чем раньше, число электронов. Однако это запрещено правилами квантования. Поэтому уровень расщепляется на N невырожденных энергетических уровней (рис.5.5), расстояние между которыми настолько мало, что переход с одного на другой почти не требует затрат энергии. В этом смысле распределение электронов по энергиям можно считать непрерывным. Совокупность уровней, на которые расщепился N-кратный уровень, называется энергетической зоной. Такие зоны показаны на рис.5.5, б.
Соседние зоны, разделенные интервалами энергий, называются запрещенными, так как в них нет разрешенных уровней энергии.
Итак, внутри кристалла внешние электроны:
а) коллективизированы, так как из-за перекрытия орбит они могут переходить от атома к атому; б) могут занимать уровни внутри энергетической зоны;
в) число уровней внутри зоны определяется числом атомов в кристалле. Теперь возникает вопрос: как распределяются электроны по уровням
внутри зоны, какой статистике подчиняется это распределение.
Функция распределения частиц по энергиям согласно статистике Больцмана
-
f e kT
показана на рис.5.6.
При T 0, согласно этой функции, должен быть занят лишь самый низкий уровень энергии (рис.5.7, а). Все N частиц должны быть на этом уровне. Но правила квантования запрещают это, потому что
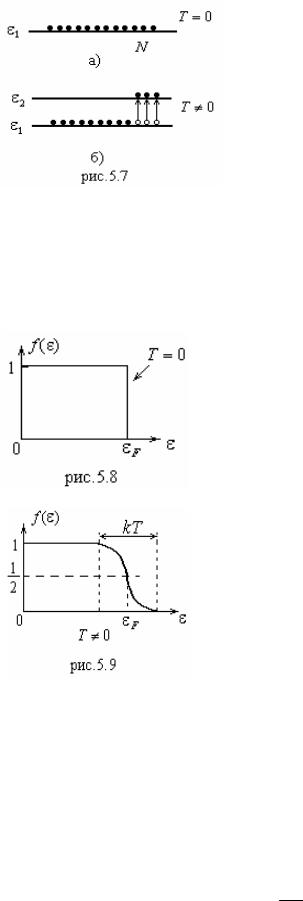
каждый уровень, согласно данным правилам, имеет лишь определенное количество мест. При повышении температуры часть частиц может занять и более высокие уровни энергии (рис.5.7, б). Из этого рассуждения ясно, что электроны не могут подчиняться статистике Больцмана.
Газ коллективизированных электронов – квантовый газ, подчиняющийся статистике ФермиДирака. Основные положения этой
статистики рассмотрим без вывода.
1. Распределение электронов по энергиям следует функции.
|
1 |
|
|
||
|
f ( ) |
|
|
, |
(5.23) |
|
|
F |
|||
где F |
1 e |
kT |
|
|
|
- энергия Ферми. Эта функция при T 0 показана на рис.5.8, так |
|||||
|
как: |
|
|
|
|
T 0 |
F ; |
f ( ) 1 |
||
|
|
; |
. |
|
|
|
F |
f ( ) 0 |
|
|
|
|
|
|
Энергия Ферми – самый высокий энергетический уровень, занятый электронами при T 0. Все уровни энергии выше F полностью свободны. Все уровни энергии ниже F полностью заняты. Если T 0, то функция (5.23) имеет вид, представленный на рис.5.9, так как:
F ;
T 0 F ;
;
F
f ( ) 1 f ( ) 1/2 f ( ) 0
Ясно, что зона “размытия” распределения существует, поскольку энергии kT достаточно, чтобы перебросить электроны на свободные энергетические уровни, т.е. по ширине она
kT .
2.Величина энергии Ферми может быть рассчитана.
Введем фазовое пространство электрона – шестимерное пространство с координатными осями, на которых откладываются пространственные координаты x, y,z и соответствующие проекции импульса электрона px , py , pz . Кинетическая энергия электрона:
p2 .
2m
Импульс электрона:
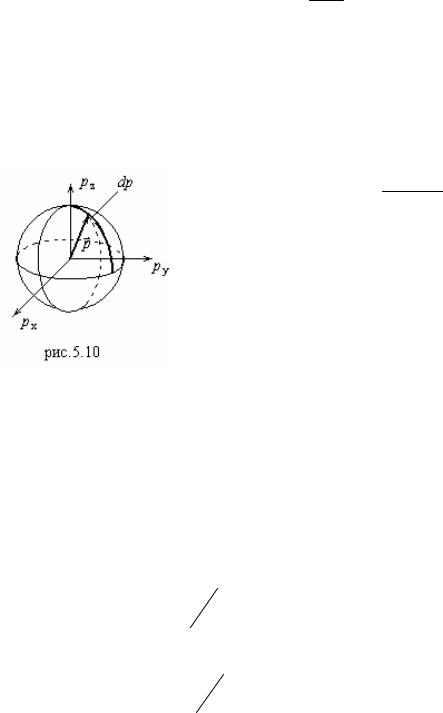
p 
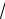 2m . (5.24)
2m . (5.24)
В фазовом пространстве точки, отвечающие значениям const должны
помещаться на |
сфере радиуса (5.24) (рис.5.10). В интервале энергий |
0 F должны |
при T 0 разместиться все N электронов. Рассчитаем |
число мест для электронов в фазовом пространстве в интервале импульсов p p dp. Это объем сферического слоя ширины dp, деленный на объем
одной элементарной ячейки в фазовом пространстве и умноженный на 2.
dN 2 4 p2dp. h3 /V
Здесь учтено, что в одной фазовой ячейке объема h3 /V располагаются 2 электрона. Тогда общее число мест, занятых электронами:
N |
|
8 |
pF |
|
n |
p2dp, |
|||
V |
h3 |
|||
|
0 |
где n - концентрация электронов в единице
объема. Отсюда:
3 |
|
3h |
3n |
|
|
pF |
|
|
|
. |
(5.25) |
|
|
||||
|
|
8 |
|
||
Таким образом, величина энергии Ферми равна:
|
|
|
|
|
|
|
|
pF2 |
|
h2 |
3n |
2 |
|
|
|
|
||||
|
|
|
|
|
EF |
|
|
3 |
. |
|
|
(5.26) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2m |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
8m |
|
|
|
|
|
|
|||||
Для того чтобы оценить величину |
EF , |
рассчитаем так |
называемую |
|||||||||||||||||
температуру Ферми: |
EF kTF и приведем ее значения в таблице для |
|||||||||||||||||||
ряда металлов. Здесь |
Ne |
- число электронов на атом, |
E |
|
- энергия |
|||||||||||||||
|
|
|
|
Na |
|
|
|
|
|
|
|
|
|
|
|
F |
|
|||
Ферми, TF - температура Ферми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вещество |
|
|
Ne |
|
|
|
EF , эВ |
|
|
|
|
TF 10 3 K |
|
|
|
||||
|
|
|
|
Na |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Li |
|
|
1 |
|
|
|
4.7 |
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Na |
|
|
1 |
|
|
|
3.1 |
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cu |
|
|
1 |
|
|
|
7.0 |
|
|
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ag |
|
|
1 |
|
|
|
5.5 |
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Au |
|
|
1 |
|
|
|
5.5 |
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Расчет проведен для следующих значений: |
|
|
|
|
|
|||||||||||||||
n 1029 м 3; |
h 10 34 |
Дж с; |
m 10 30 |
кг; |
|
1эВ 10 19 Дж. |
||||||||||||||
Видно, что T TF , |
поэтому зона |
“размытия” |
распределения Ферми |
|||||||||||||||||
(рис.5.9) kT kTF |
EF . |
Практически |
все электроны |
в |
металлах |
|||||||||||||||
находятся на полностью занятых уровнях энергии. Из графика рис.5.9 видно, что лишь в зоне “размытия” и выше по энергиям есть свободные уровни, остальные электроны не могут изменить своей энергии, т.е. не могут участвовать в процессах теплопереноса. Число термически активированных электронов NT :
NT |
|
kT |
|
|
kT |
10 |
3 |
|
|
|
|
|
|
; |
NT |
N |
|
|
N |
(5.27). |
|
N |
|
F |
|
|||||||
|
F |
|
|
|
|
|
|
|||
Ранее была выведена формула Друде (5.8) для электропроводности, которая теперь может быть записана в ином виде:
n e2 , m
где время релаксации заменено выражением / ; здесь - длина свободного пробега; - скорость. В силу вышесказанного F ; так как средняя кинетическая энергия
электрона |
m 2F |
F . На рис.5.11 |
|
||
2 |
|
|
представлена зависимость функции распределения f ( ) по скоростям от скорости x. Из рис. видно, что возможны два знака при одном и
том же значении энергии. При этом число электронов n n .
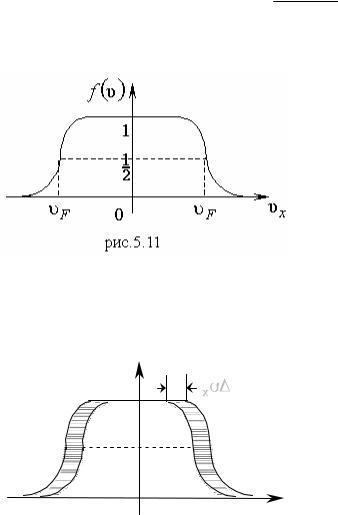
3. Рассмотрим, как изменится это распределение, если кристалл внести во внешнее электрическое поле E Ex . Электрон приобретает добавочную
скорость:
f ( x ) |
m x |
eEx ; |
1 |
|
|
|
|
|
|
|
|
x |
eEx |
F . |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
m |
||||
|
2 |
|
|
|
x |
Оценка дает значение: |
||||
|
|
рис. 5.12 |
F ~106 -107 м/с; |
|||||||
|
|
|
|
|
|
|||||
x |
|
eE |
|
10 19 |
10 1 10 14 |
10 4 м/с при T 300 К. |
||||
|
|
|
|
10 30 |
||||||
|
|
m |
|
|
|
|||||
Распределение f ( x ) сместится в сторону x 0 на x (рис.5.12). Электроны в заштрихованной области при x 0, имея большую энергию, будут стремиться занять места с меньшей энергией в заштрихованной области с x 0. Появится ток, при этом электроны будут двигаться в направлении, противоположном приложенному полю.
