Линейная модель парной регрессии и корреляции

.

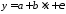Построение линейной регрессии сводится к оценке ее параметров – и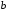. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметрови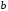, при которых сумма квадратов отклонений фактических значений результативного признака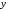от теоретическихминимальна:

.

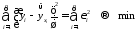свойства оценок, полученных с помощью МНК:

1. Линейность оценок – оценки параметров 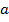ипредставляют собой линейные комбинации наблюдаемых значений объясняемой переменной.

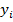2. Несмещённость оценок:

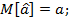
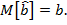
3. Состоятельность оценок:

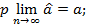
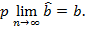
4. Эффективность – данное свойство означает, что оценка имеет минимальную дисперсию в заданном классе оценок:

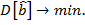
Теорема Гаусса-Маркова: если выполнены условия Гаусса-Маркова, тогда оценки , полученные с помощью метода наименьших квадратов, являются линейными, несмещёнными, эффективными и состоятельными оценками.

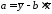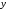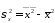,, где ковариация признакови,– дисперсия признакаи

Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.

Параметр 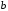называетсякоэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально – значение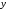при.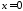

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейныйкоэффициент корреляции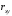, который можно рассчитать по следующим формулам:

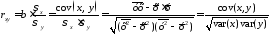. (1.6)

Для оценки качества подбора линейной функциирассчитывается квадрат линейного коэффициента корреляции, называемыйкоэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии результативного признака.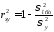

Чтобы иметь общее суждение о качестве моделииз относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации. не должна превышать 8–10%.

После того как найдено уравнение линейной регрессии, проводится оценка значимостикак уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. на основе-критерия Фишера, которому предшествует дисперсионный анализ.

13.Сравнение истинных и оцененных зависимостей

14.Множественная линейная регрессия

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии

,

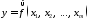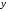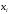где – зависимая переменная (результативный признак),– независимые, или объясняющие, переменные (признаки-факторы).