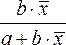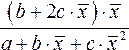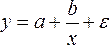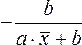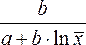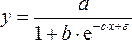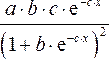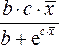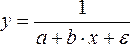17.Частные уравнения регрессии. Частные коэффициенты эластичности

На основе уравнения (2.1) могут быть найдены частные уравнения регрессии:

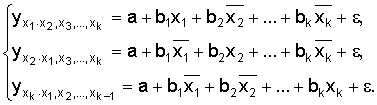. (2.4)

Частные уравнения регрессии характеризуют изолированное влияние фактора, при условии, что остальные закреплены на неизменном уровне.

Если в (2.4) подставить , то система (2.4) будет иметь вид:

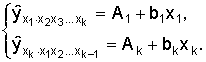
коэффициентов эластичности для различных типов уравнений регрессии.

В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы для наиболее часто используемых типов уравнений регрессии приведены в таблице:

Вид функции,	Первая производная,	Средний коэффициент эластичности,

Только для степенных функций коэффициент эластичности представляет собой постоянную независящую отх величину, равную в данном случае параметру b.

Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Например, на сколько процентов изменится заработная плата с ростом стажа работы на 1%? В такой ситуации степенная функция, даже если она оказывается наилучшей, не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита у (в процентах годовых) и срока его предоставления х (в днях), было получено уравнение регрессии с очень высоким показателем корреляции (0,98). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает (в процентах) изменение ставок кредита с увеличением срока его предоставления на один день.

В линейной модели множественной регрессии если факторные признаки различны по своей сущности или имеют различные единицы измерения, коэффициенты регрессии b_j являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям относятся частные коэффициенты эластичности.

Частные коэффициенты эластичности рассчитываются по формуле:

,

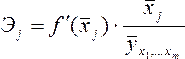где - среднее значение фактора;

- среднее значение результата у.

Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется результат у с увеличением фактора на 1% от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости коэффициенты эластичности рассчитываются по формуле:

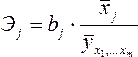
где – коэффициент регрессии для факторав уравнении множественной регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:

,

которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

18.Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками, обобщённый метод наименьших квадратов 1.Задачи эконометрики в области социально-экономических исследований. 2.Эконометрика и её связь с экономической теорией. Эконометрический анализ в макроэкономике. 3.Этапы развития эконометрики. Показать полностью.. 4.Экономические данные: перекрёстные данные и временные ряды. Цели и методы сбора статистических данных. 5.Подготовка статистических данных и использование их в модели. 6.Различные способы представления экономических данных. 7.Введение случайного компонента в экономическую модель. Эконометрическая модель. Адекватность, точность, область применения. 8.Классификация переменных в эконометрических моделях. 9.Понятия спецификации и идентифицируемости модели. 10.Корреляционная зависимость. Модельное и выборочное уравнение регрессии. 11.Парная линейная регрессия. Метод наименьших квадратов (МНК). Свойства оценок МНК. 12.Парная линейная регрессия. МНК. Предпосылки МНК. 13.Сравнение истинных и оцененных зависимостей. 14.Множественная линейная регрессия. 15.Показатели качества регрессии. 16.Частные уравнения регрессии. Частные коэффициенты корреляции. 17.Частные уравнения регрессии. Частные коэффициенты эластичности. 18.Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками, обобщённый метод наименьших квадратов. 19.Проверка общего качества уравнения парной линейной регрессии. 20.Проверка общего качества уравнения нелинейной регрессии. 21.Проверка общего качества уравнения множественной регрессии. 22.Проверка качества параметров парной регрессии. 23.Проверка качества параметров множественной регрессии. 24.Целесообразность применения множественной регрессии. Отбор факторов в модель. 25.Уравнение регрессии в стандартизованном масштабе переменных. 26.Автокорреляция остатков. Статистика Дарбина-Уотсона. 27.Обобщенный, взвешенный метод наименьших квадратов. 28.Проверка наличия гетероскедастичности остатков, метод Гольдфельда-Квандта. 29.Системы одновременных уравнений. 30.Структурная и приведенная форма модели. 31.Нелинейные модели регрессии и их линеаризация. 32.Идентифицируемость систем одновременных уравнений. 33.Косвенный, двухшаговый и трёхшаговый метод наименьших квадратов. 34.Классификация временных рядов. Характеристики временных рядов. 35.Тренды и сезонные изменения. 36.Аддитивная и мультипликативная модель временного ряда. 37.Сглаживание временных рядов. 38.Определение параметров тренда временного ряда. 39.Модели авторегрессии и их идентификация1.Задачи эконометрики в области социально-экономических исследований. 2.Эконометрика и её связь с экономической теорией. Эконометрический анализ в макроэкономике. 3.Этапы развития эконометрики. Показать полностью.. 4.Экономические данные: перекрёстные данные и временные ряды. Цели и методы сбора статистических данных. 5.Подготовка статистических данных и использование их в модели. 6.Различные способы представления экономических данных. 7.Введение случайного компонента в экономическую модель. Эконометрическая модель. Адекватность, точность, область применения. 8.Классификация переменных в эконометрических моделях. 9.Понятия спецификации и идентифицируемости модели. 10.Корреляционная зависимость. Модельное и выборочное уравнение регрессии. 11.Парная линейная регрессия. Метод наименьших квадратов (МНК). Свойства оценок МНК. 12.Парная линейная регрессия. МНК. Предпосылки МНК. 13.Сравнение истинных и оцененных зависимостей. 14.Множественная линейная регрессия. 15.Показатели качества регрессии. 16.Частные уравнения регрессии. Частные коэффициенты корреляции. 17.Частные уравнения регрессии. Частные коэффициенты эластичности. 18.Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками, обобщённый метод наименьших квадратов. 19.Проверка общего качества уравнения парной линейной регрессии. 20.Проверка общего качества уравнения нелинейной регрессии. 21.Проверка общего качества уравнения множественной регрессии. 22.Проверка качества параметров парной регрессии. 23.Проверка качества параметров множественной регрессии. 24.Целесообразность применения множественной регрессии. Отбор факторов в модель. 25.Уравнение регрессии в стандартизованном масштабе переменных. 26.Автокорреляция остатков. Статистика Дарбина-Уотсона. 27.Обобщенный, взвешенный метод наименьших квадратов. 28.Проверка наличия гетероскедастичности остатков, метод Гольдфельда-Квандта. 29.Системы одновременных уравнений. 30.Структурная и приведенная форма модели. 31.Нелинейные модели регрессии и их линеаризация. 32.Идентифицируемость систем одновременных уравнений. 33.Косвенный, двухшаговый и трёхшаговый метод наименьших квадратов. 34.Классификация временных рядов. Характеристики временных рядов. 35.Тренды и сезонные изменения. 36.Аддитивная и мультипликативная модель временного ряда. 37.Сглаживание временных рядов. 38.Определение параметров тренда временного ряда. 39.Модели авторегрессии и их идентификация1.Задачи эконометрики в области социально-экономических исследований.Задачи эконометрики в области социально-экономических исследованийЗадачи эконометрики в области социально-экономических исследований