гл1

12

1. Способы задания логических функций

Функция , зависящая от n переменных , называется логической или переключательной, если функция и любой из ее аргументов принимают значения только из множества {0,1}. Аргументы логической функции также называются логическими.

Рассмотрим три способа задания логической функции: матричный (табличный), геометрический и аналитический. При матричном способе логическая функция n переменных задается таблицей истинности, в левой части которой перечислены все наборов значений переменных, а в правой части – значение функции на этих наборах. Например, табл. 1.1 задает функцию трех переменных .

Д

Таблица 1.1

Номер набора
0	0	0	0	0
1	0	0	1	1
2	0	1	0	1
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	0
7	1	1	1	0

воичный набор можно рассматривать как целое число N: , называемое номером набора . Поэтому иногда в таблице истинности логической функции наборы представляются их номерами. Часто для сокращения записи логическую функцию задают вектором , в котором координата представляет собой значение функции на наборе (на наборе с номером i), т.е. логической функции взаимно однозначно соответствует двоичный вектор длины , следовательно, существует различных логических функций от n переменных. Вектор также иногда задают в виде его десятичного эквивалента. Таким образом, при задании логической функции (см. табл. 1.1) можно использовать запись(01110100) или 116.

Логические функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Поэтому, для задания функций многих переменных удобно использовать модификацию таблицы истинности. Для этого множество из n переменных функции разбивается на два подмножества и . В этом случае, n-мерное пространство¹⁾ с образующими , представляется в виде декартова произведения двух пространств  с образующими и соответственно.

Т

Таблица 1.2

	00	01	10	11
0	0	1	1	1
1	0	1	0	0

огда логическую функцию можно задать в виде двумерной таблицы: каждому значению переменных , ,..., взаимно однозначно соответствует строка таблицы, столбцу – значения переменных , ,..., и на пересечении i-й строки и j-го столбца, взаимно однозначно соответствующем точке n-мерного пространства с образующими , записывается значение функции в этой точке. Например, функция, представленная табл.1.1, может быть задана табл.1.2, где множество разбито на два подмножества и .

При геометрическом способе логическая функция задается с помощью гиперкуба ( n-мерного куба ).

Гиперкубом называется граф, каждая вершина которого взаимно однозначно соответствует точке пространства - двоичному вектору (набору), и две вершины соединены ребром, если соответствующие им двоичные векторы отличаются в одном и только одном разряде.

Отмечая вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, логическая функция, заданная табл.1.1, геометрически представляется 3-мерным кубом на рис.1.1.

Если на некоторых наборах значений переменных логическая функция не определена (т.е., на данном наборе значение функции может быть как 0, так и 1), то она называется частичной. Доопределением частичной функции f называется всякая (всюду определенная) логическая функция, совпадающая с f там, где значения f заданы. В табл. 1.3 приведена частичная функция f и все возможные ее доопределения , , , .

При задании частичной функции обычно перечисляют наборы из области ее определения и указывают значения функции на каждом из них (табл. 1.4). Часто используется задание в виде двух таблиц, в одной из которых перечисляются наборы, где функция равна 1, а в другой – наборы с нулевым значением функции.

Рис. 1.1

Таблица 1.3

	f
0 0	1	1	1	1	1
0 1	*	0	0	1	1
1 0	0	0	0	0	0
1 1	*	0	1	0	1

Таблица 1.4

	f
0 0	1
1 0	0

Прежде чем рассматривать аналитический способ задания логических функций, рассмотрим наиболее употребляемые логические функции одной и двух переменных (элементарные функции). Функции одной переменной представлены в табл.1.5, функции двух переменных – в табл.1.6. Приведем обозначения и названия этих функций.

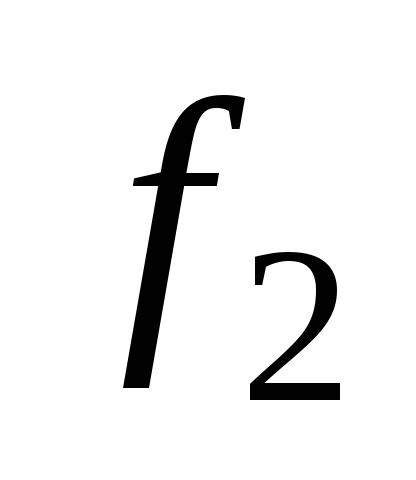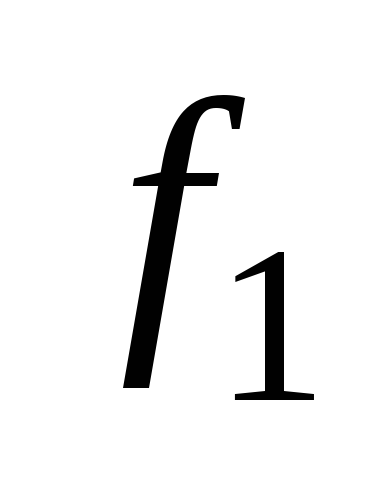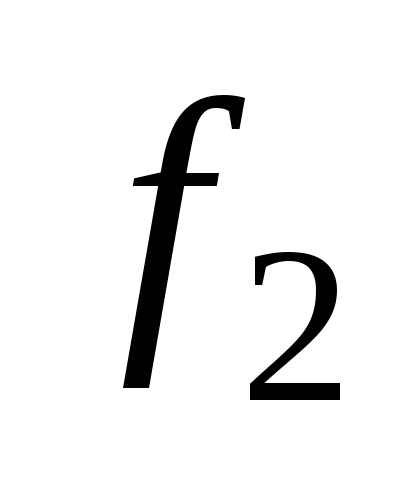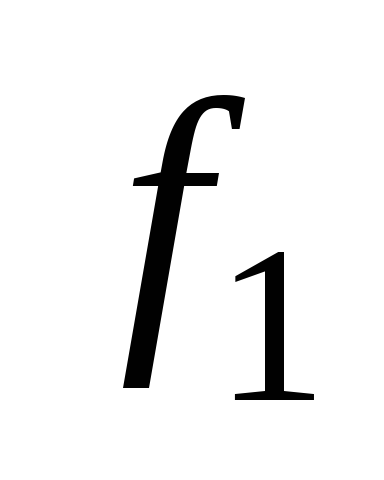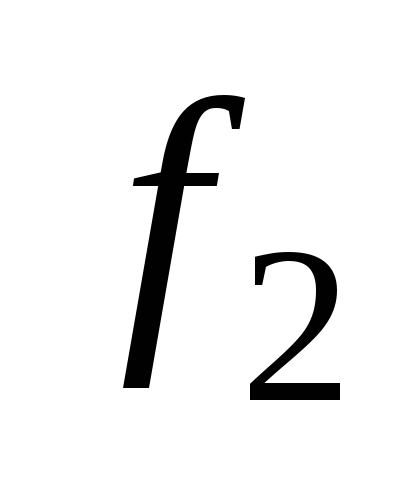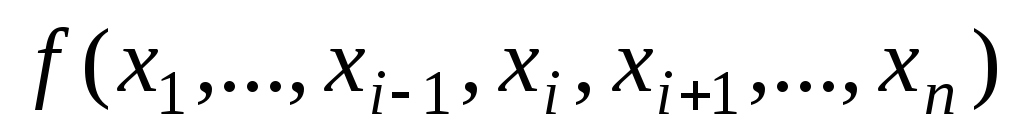1. Функции (x)=0 и (x)=1 называются соответственно тождественным нулем и тождественной единицей. Заметим, что и не зависят от переменной x, поэтому их иногда рассматривают как функции, зависящие от пустого множества переменных. Функцию еще называют константой 0, а – константой 1. Переменная x в данном случае является фиктивной. В общем случае переменная в функции называется фиктивной (несущественной), если

=

при любых значениях остальных переменных.

Таблица 1.6

0 0	0	0	0	1	1	1	1
0 1	0	1	1	0	1	1	0
1 0	0	1	1	0	0	1	0
1 1	1	1	0	1	1	0	0

Таблица 1.5

0	0	1	0	1
1	0	1	1	0

2. Функция (x) называется тождественной функцией и обозначается через x.

3. Функция (x) называется отрицанием x, обозначается ,  x, x’ и часто читается "не x".

4. Функция называется конъюнкцией, обозначается &, , , , или min(,) и часто читается «и».

5. Функция называется дизъюнкцией, обозначается , + или max(,) и часто читается «или».

6. Функция называется суммой по модулю 2, обозначается ,  и часто читается " плюс "¹⁾. Так как данная функция равна 1, когда ее аргументы различны, и равна 0, когда они равны, то ее иногда называют неравнозначностью.

7. Функция называется эквивалентностью или равнозначностью. Ее обозначения: ,  или , читается " эквивалентно ".

8. Функция называется импликацией. Обозначения , ; читается "если , то " или " имплицирует ".

9. Функция называется штрихом Шеффера, обозначается  и часто читается "не и ".

10. Функция называется стрелкой Пирса (функция Вебба), обозначается , читается "не или ".

Теперь рассмотрим аналитический способ задания логической функции, при котором логическая функция f задается суперпозицией других функций (формулой).

Суперпозицией функций называется функция f, полученная с помощью подстановок этих функций друг в друга и переименования переменных, а формулой называется выражение, описывающее эту суперпозицию. Понятие суперпозиции очень важно в алгебре логики, поэтому рассмотрим его более подробно.

Пусть дано множество (конечное или бесконечное) исходных функций . Символы переменных будем считать формулами глубины 0. Формула F имеет глубину , если F имеет вид , где , t - число аргументов , а – формулы, максимальная из глубин которых равна k. называется подформулами F; называется внешней или главной операцией формулы F. Все подформулы формул также называются подформулами F. Например, (x), и – это формулы глубины 1, а – формула глубины 3, содержащая одну подформулу глубины 2 и две подформулы глубины 1.

В дальнейшем конкретные формулы, как правило, будут иметь более привычный вид, при котором знаки функций стоят между аргументами. Такую запись называют инфиксной, то есть формулу вида f (x,y) записывают либо как (x f y), либо как x f y, а формулу f (x) - как (f x) или f x. При этом символы f называют связками. Обычно в качестве связок употребляются символы из множества G={,&,,,,,,}, то есть символы, обозначающие рассмотренные выше элементарные функции.

Например, если обозначает отрицание ( ), – дизъюнкцию (), – конъюнкцию (&), а – импликацию (), то приведенная ранее формула примет вид

((x)(z(x&y))). (1.1)

Для сокращения записи формул над множеством связок G принято следующее соглашение:

а) внешние скобки у формул опускаются;

б) формула (F) записывается в виде ;

в) формула (&) записывается в виде  или ;

г) считается, что связка  сильнее любой двухместной связки из G;

д) связка & считается сильнее, чем любая из связок , , , , , .

Эти соглашения позволяют, например, формулу (1.1) записать в виде

(1.2)

Употребляется и смешанная запись формул, например, xf(y,z) или .

Всякая формула, выражающая функцию f как суперпозицию других функций, задает способ ее вычисления (при условии, что известно, как вычислить исходные функции). Вычислим, например, формулу (1.2) на наборе x=0, y=1, z=1. Получим (используя табл. 1.5 и 1.6): xy=0; zxy=z0=1; =1; (zxy)=11=1.

Таким образом, формула каждому набору значений аргументов ставит в соответствие значение функции и, следовательно, может служить наряду с таблицей способом задания и вычисления функции. В частности, по формуле, вычисляя ее на всех наборах, можно восстановить таблицу функции.

О формуле, задающей функцию, также говорят, что она реализует или представляет эту функцию. Если функция f частична, то считается, что формула реализует f, если она реализует какое-либо ее доопределение.

В отличие от табличного и геометрического задания представление данной функции формулой не единственно. Например, если в качестве исходного множества связок зафиксировать множество {,&,}, то функцию штрих Шеффера ( в табл. 1.6) можно представить формулами:  и , а функцию стрелка Пирса () - формулами и .