2. Если строить автомат, реализующий данную ограниченно-детерминированную функцию, через информационное дерево, то получится автомат, все состояния которого отличимы.
Логично задаться вопросом: сколько и
каких последовательностей достаточно
подавать на вход автомата, чтобы
установить отличимость двух его
состояний? Ответ на этот вопрос дает
теорема Мура, которую мы приводим ниже
без доказательства.
Рассмотрим автомат
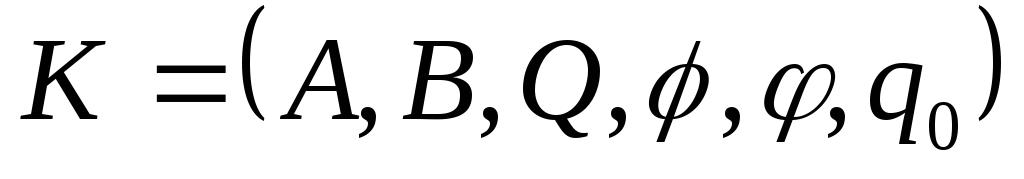
Определение. Пусть
 .
Говорят, что состояния
.
Говорят, что состояния
 и
и
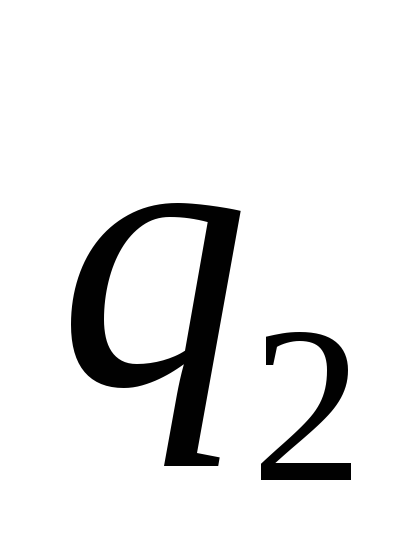 автомата
автомата
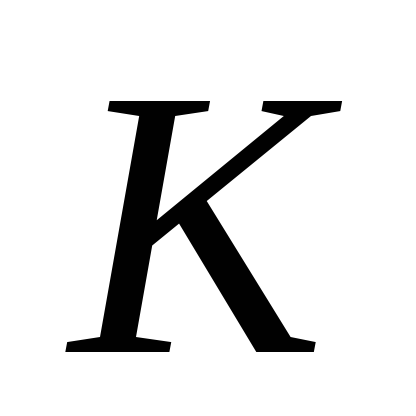 отличимы множеством
отличимы множеством
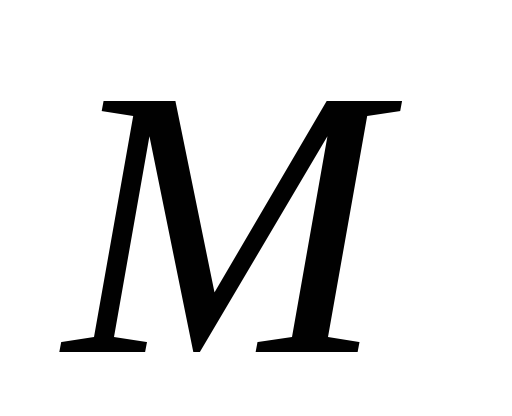 ,
если
,
если
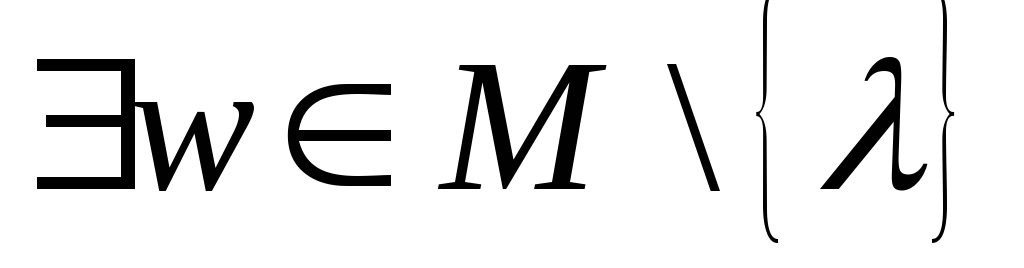 такое, что
такое, что
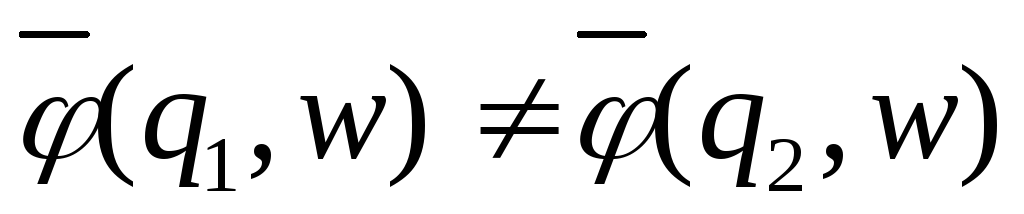 .
В противном случае говорят, что состояния
.
В противном случае говорят, что состояния
 и
и
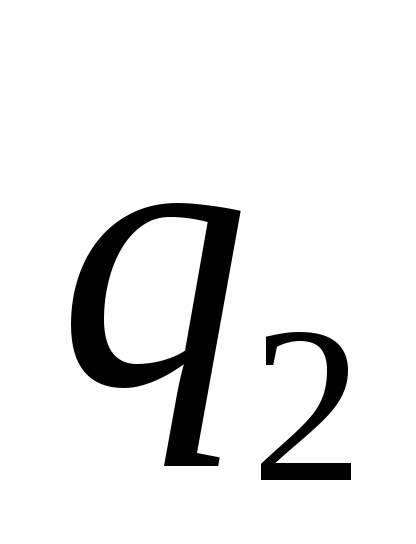 неотличимы множеством
неотличимы множеством
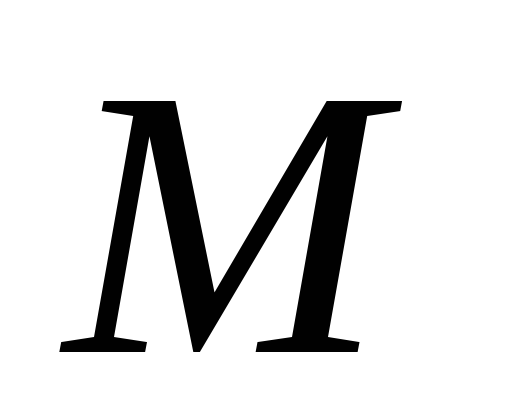 .
.
Заметим, что
обычная отличимость – это отличимость
с помощью множества
 .
.
Теорема (Мура). Если состояния
 и
и
 автомата
автомата
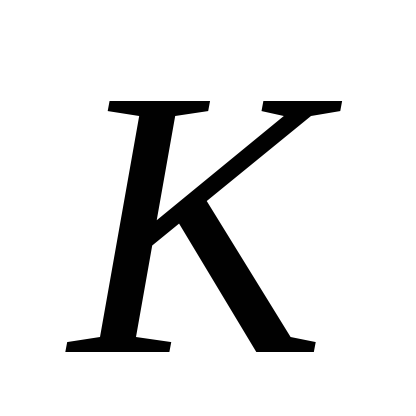 отличимы, то они отличимы и множеством
отличимы, то они отличимы и множеством
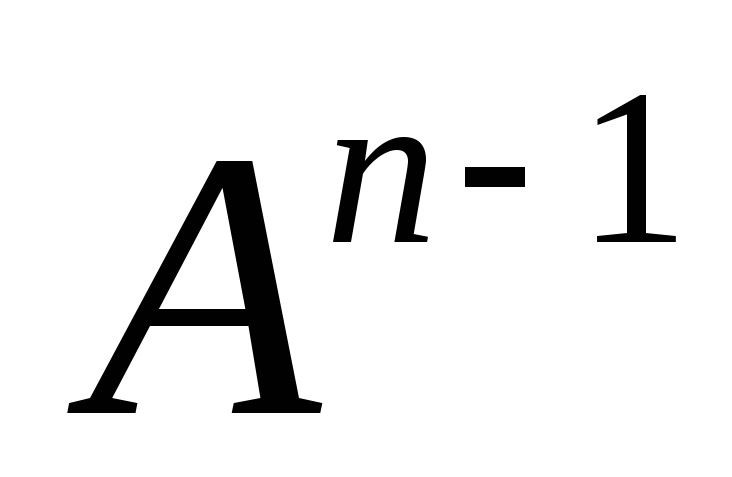 ,
где
,
где
 .
.
Пример 3.
Рассмотрим автомат, заданный таблицей
1. Согласно теореме Мура, чтобы выявить
отличимые состояния этого автомата
достаточно посмотреть отличимость
состояний автомата словами длины 1.
Состояние
 отличимо от состояний
отличимо от состояний
 ,
,
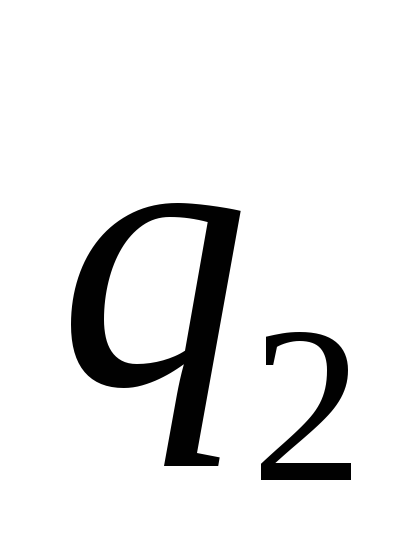 ,
,
 ,
,
 словом 0. Состояния
словом 0. Состояния
 ,
,
 отличимы от состояний
отличимы от состояний
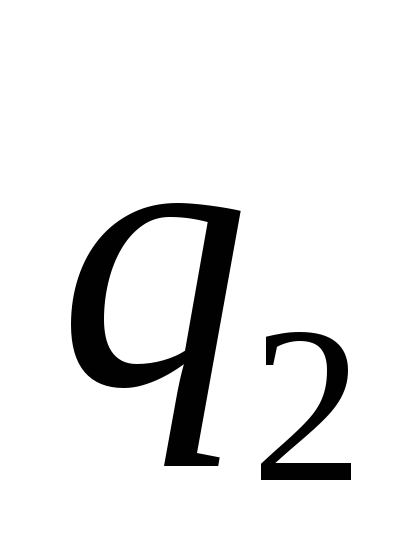 ,
,
 словом 1. Следовательно, имеем три
различные классы эквивалентности
автомата по отношению отличимости:
словом 1. Следовательно, имеем три
различные классы эквивалентности
автомата по отношению отличимости:
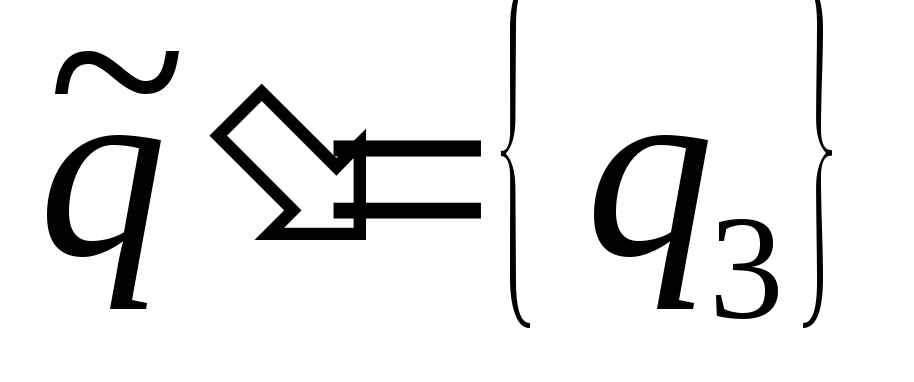 ,
,
 ,
,
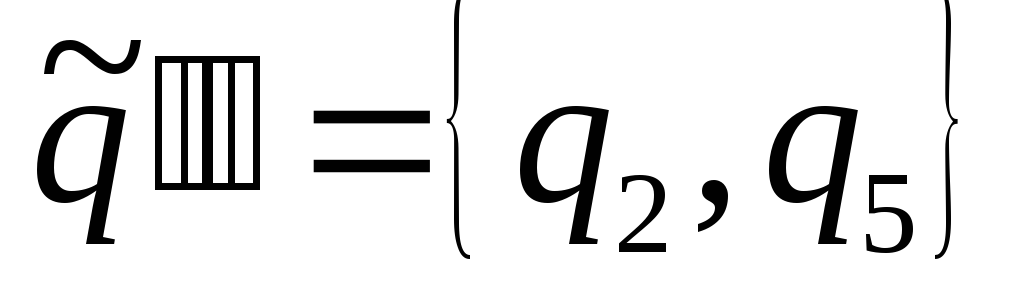 .
Таким образом, множество состояний
приведенного автомата, соответствующего
данному, имеет три элемента
.
Таким образом, множество состояний
приведенного автомата, соответствующего
данному, имеет три элемента
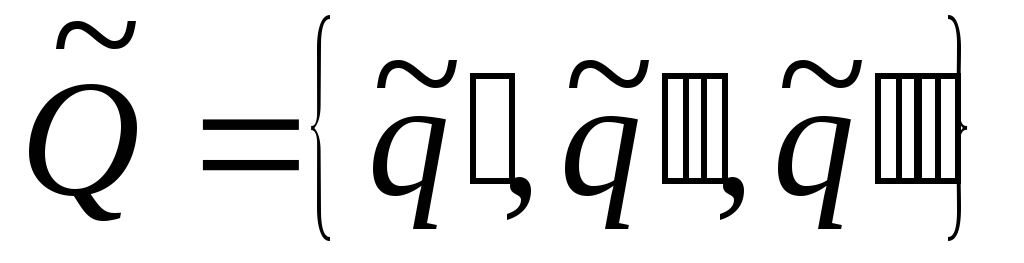 ,
а его работа описывается таблицей 2.
,
а его работа описывается таблицей 2.
Таблица 1
Таблица 2
74


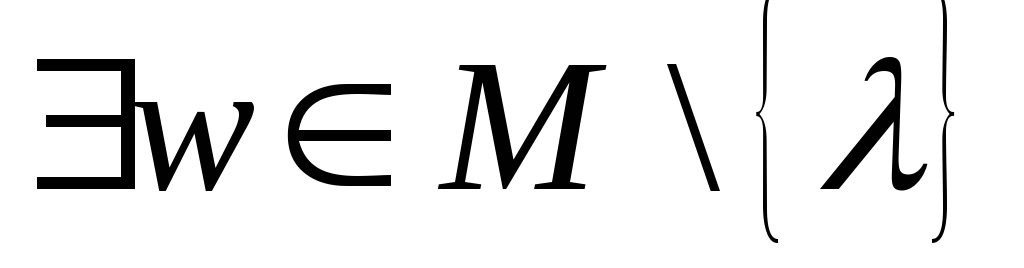 такое, что
такое, что