4.2. Реализация ограниченно-детерминированных функций конечными автоматами

Рассмотрим произвольную ограниченно-детермиированную функцию . Функция может быть интерпретирована как функция, описывающая работу дискретного преобразователя информации. На входы этого преобразователя в моменты времени подаются члены последовательности . В эти же моменты времени на выходе возникают члены последовательности , где . Такой дискретный преобразователь называют конечным автоматом, реализующим функцию . При формальном определении математической модели автомата будем исходить из задания ограниченно-детерминированной функции совокупностью функций и .

Определение. Конечным автоматом Мили называется шестерка объектов , где

- конечное непустое множество (входной алфавит);

- конечное непустое множество (выходной алфавит);

- конечное непустое множество (множество состояний);

- отображение, называемое функцией переходов;

- отображение, называемое функцией выходов;

- начальное состояние.

При этом последовательность называют входной последовательностью, последовательность - выходной последовательностью; буквы и называют сигналами, поступившими в момент времени соответственно на вход и на выход рассматриваемого автомата.

Способы задания автоматов те же, что и способы задания ограниченно-детермиированных функций.

1. Поскольку функции и определены на конечных множествах, их удобно задавать с помощью таблицы. Пусть , , тогда таблица автомата имеет вид:

			…
			…
			…
…	…	…	…	…
			…

Чтобы полностью определить автомат, нужно также указать его начальное состояние.

2. Задают автоматы и с помощью диаграммы Мура, т.е. геометрического графа, определенного следующим образом: каждому состоянию автомата сопоставляется вершина графа; если для двух состояний , существует входной сигнал , такой что , то из вершины в вершину проводится дуга, помечаемая двойной меткой , где .

Чтобы полностью определить автомат, нужно также указать на графе вершину, соответствующую его начальному состоянию.

3. Задать автомат можно и системой канонических уравнений:

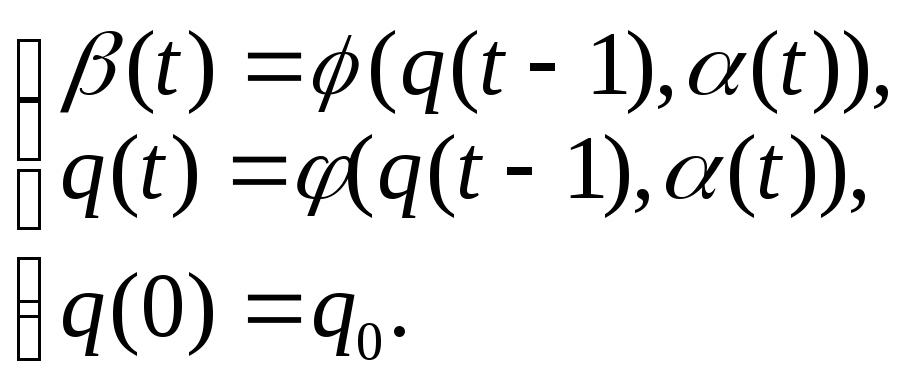
Рассмотрим некоторые виды конечных автоматов.

1. Автомат без памяти – автомат, в котором множество состояний включает ровно один элемент, т.е. . Тогда функция переходов всегда принимает одно и то же значение , и ее можно не рассматривать. Функция выходов зависит фактически только от входного сигнала. Работу автомата можно описать только одним каноническим уравнением: . Так, в частности, работает автомат, который осуществляет перекодировку символов из одного алфавита в другой.

2. Элемент задержки – автомат, у которого входной и выходной алфавиты совпадают, причем , для любого момента времени , . Несложно построить канонические уравнения такого автомата, задав их, например, так:

Если же мы хотим описать такой автомат, исходя из определения, то будем иметь: ; , .

Пример 1. Рассмотрим частный случай элемента задержки .

Таблица автомата: Диаграмма Мура автомата:

	0	1
0	0 0	1 0
1	0 1	1 1

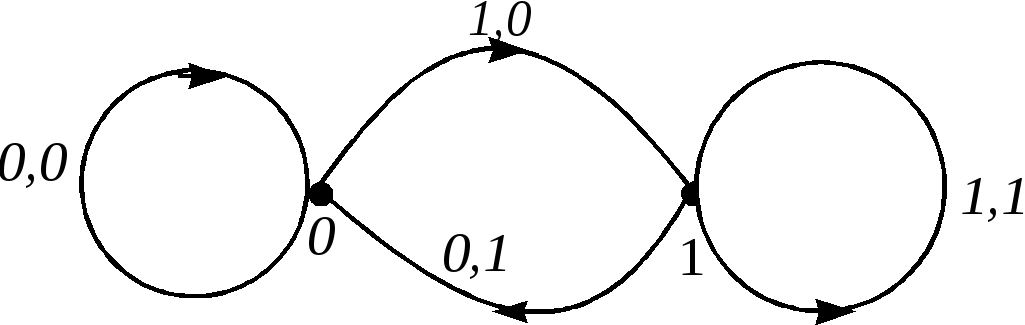
В качестве начального состояния элемента задержки можно взять любое из его состояний. Пусть начальное состояние автомата 0 и на его вход подается последовательность 1010101010…, тогда на выходе автомата наблюдается 0101010101…

Замечание. Конечный автомат Мили определен таким образом, что каждый автомат реализует конкретную ограниченно-детермированную функцию, однако одна и та же ограниченно-детерминированная функция может быть реализована различными автоматами. Остановимся на этом вопросе подробнее.