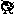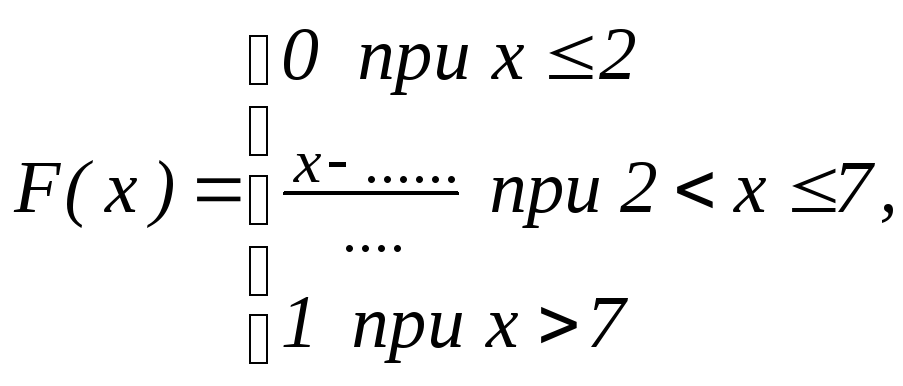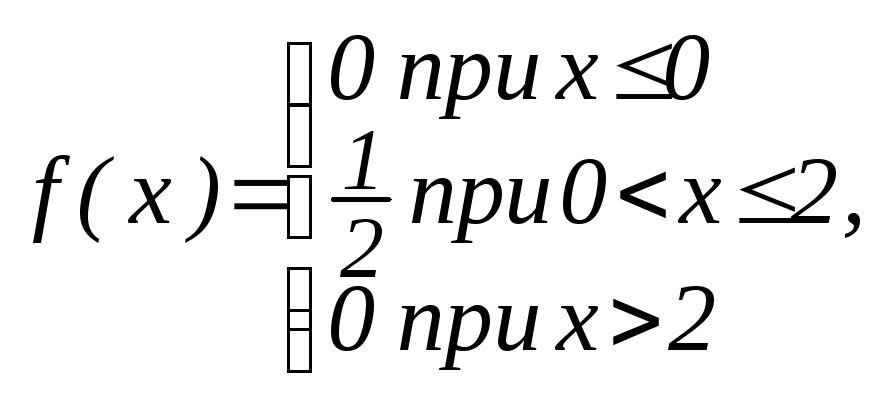Глава девятая Нормальное распределение

§1. Равномерное распределение

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Пусть случайная величина Х принимает значения из интервала (а,b), на котором плотность равномерного распределения f(x) = c. Найдем с. Т.к. все возможные значения Х принадлежат (а,b), то или, откуда. Итак,(*)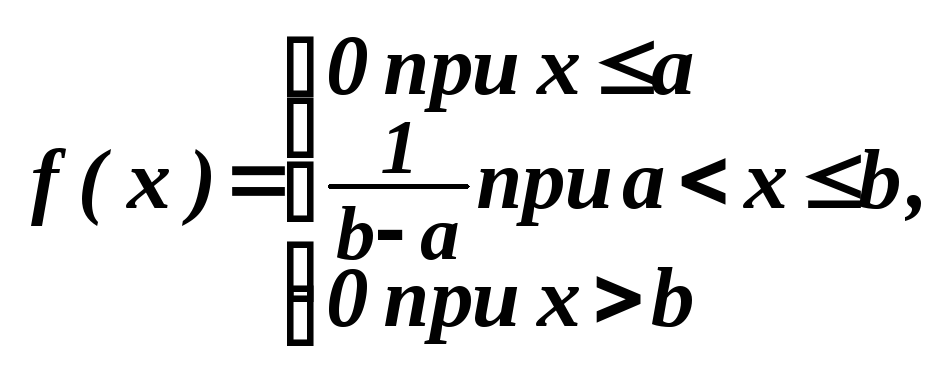

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания.

В главе 7 п.3. для f(x), заданной (*), найдена F(x), а именно:

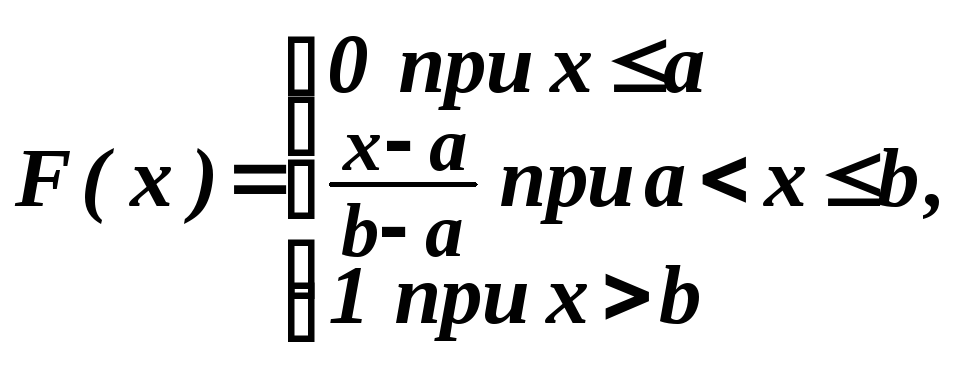
График функции распределения	График плотности распределения

Случайная величина равномерно распределена на отрезке [a,b]. Найдите функцию F(x) и запишите плотность распределения f(x) этой случайной величины.

№	а	в	в - а	F(x)	f(x)
1	2	7	…
2	2	3

Можно вычислить математическое ожидание и дисперсию случайной величины, имеющей равномерный закон распределения, а именно: (Гл.8, §3)

Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше 0,5 минуты? Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х – времени ожидания поезда.

а	в	в - а	f(x)		M(X)	D(X)
0	2	…		=……	= =… 1(мин)		0,58 мин

§2. Нормальное распределение

Непрерывная случайная величина Х имеет нормальный закон распределения, если ее плотность вероятности имеет вид: , гдеа – математическое ожидание, - среднее квадратическое отклонение.

Кривую нормального распределения называют нормальной кривой или кривой Гаусса.

Свойства функции.

1. D(f) = R

2. При всех значениях аргумента функция принимает положительные значения.

3. , т.е. ось Ох является горизонтальной асимптотой графика.

4. График симметричен относительно прямой х = а ( разность х - а содержится в четной степени).

5. Исследование на экстремум.

Найдем первую производную: . Отсюда:при

х = а ( х = а – критическая точка).

х = а –точка максимума.

6. График.

Изменение параметра а не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает (Рис.1).

С возрастанием максимальная ордината кривой убывает, а сама кривая становится более пологой. При убываниимаксимальная ордината кривой увеличивается, а сама кривая становится более "островершинной" (Рис.2) .