2.7. Переход к нехудшему опорному плану.

Пусть решается ЗЛП с системой ограничений в предпочтительном виде:

(i=)

Начальный опорный план для такой задачи: . Значение целевой функции:Z=.

Пусть исходная задача решается на максимум (для ЗЛП на минимум все рассуждения аналогичны). Если все оценки () неотрицательны, то план оптимален и задача решена. Предположим, что среди оценок свободных членов есть по крайней мере одна отрицательная. Обозначим ее. Назовем соответственный вектор столбец- разрешающим, а соответственную переменную- перспективной.

Попытаемся заменить некоторую базисную переменную на . При этом все остальные свободные переменные не должны измениться.

Рассмотрим систему ограничений ЗЛП:

(i=)

Преобразуем ее следующим образом:

(i=)

Так как все свободные переменные кроме равны 0, получим:

(i=) (1).

Отсюда:

(i=).

По условию задачи линейного программирования все переменные, включая , должны быть неотрицательны. Следовательно:

(i=).

Отсюда:

(i=).

Так как базисных переменных не может быть больше m, то при внесении в базис какая-то из базисных переменных будет свободной. Пусть это переменная. Тогда:

→

По условию задачи все - неотрицательны. Тогда идолжно быть положительным.

Таким образом, базисный элемент и соответственную строкуk следует искать среди строк, которых положительны.

Не ограничивая общности, предположим, что первые s строк имеют >0. Найдем отношениедля всех этих строк. Получим последовательность чисел. Среди чисел этой последовательности выберем минимальное:

min==Θ.

Назовем это отношение наименьшим симплексным отношением. Соответствующий элемент – разрешающим и соответственную строкуk – разрешающей. Базисная переменная будет считаться неперспективной.

Вернемся к равенству (1).

(i=) (1).

Для i=k получим:

.

Отсюда:

= Θ

Тогда:

(i=).

Новый базис будет состоять из переменных ,, …, , , , …, . Соответствующий ему опорный план имеет вид:

Проверим, является ли полученный опорный план "нехудшим". Для этого найдем для нового опорного плана:

,

где – значение целевой функции первоначального опорного плана,- оценка, соответствующая столбцу. Так как<0, аΘ>0, то полученное значение целевой функции >

Алгоритм выбора разрешающего элемента для задач линейного программирования на максимум (минимум) представлен на Рис. 12.

2.8. Симплексные преобразования

Для того, чтобы перейти к новому базису необходимо выразить новую базисную переменную через свободные переменные.

Рассмотрим систему ограничений ЗЛП:

(i=)

Рис. 12. Алгоритм выбора разрешающего элемента для задач линейного программирования на максимум (минимум)

Преобразуем ее следующим образом:

(i=)

Выразим из системы базисную переменную :

.

Распишем подробнее:

Отсюда:

Тогда

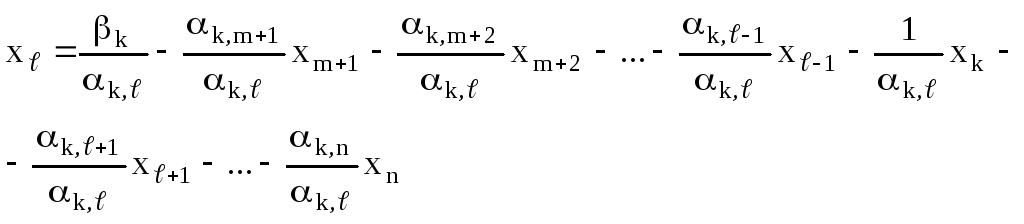
Подставим данное равенство в другие ограничения системы:

Для целевой функции формула представима в виде:

Вычисление по данным формулам получило название симплексных преобразований. Для того чтобы перейти с помощью симплексных преобразований к новому опорному плану можно действовать двумя способами.

Способ 1.

1. Найти разрешающий элемент.

2. С помощью представленных формул преобразовать все уравнения системы ограничений.

3. Посчитать значение целевой функции.

Способ 2.

Алгоритм действий представлен на Рис. 13.

Определение: Шаг симплексного метода, позволяющего перейти от одного опорного плана к другому, называется итерацией.

Пример: Решить симплексным методом ЗЛП:

при

Рис. 13. Алгоритм решения задач линейного программирования на максимум (минимум), используя симплексные преобразования

Решение.

Система ограничений имеет предпочтительный вид. Можно составлять симплексную таблицу:

БП	СБ	А						№ итерации
			14	-5	2	-1	8
	-5	5	1 \	1	0	0	-1	0
	2	41	5 \	0	1	1	3
	-1	15	-5	0	0	0	4
		42	-4	0	0	0	-1
	14	5	1	1	0	0	-1	1
	2	16	0	-5	1	0	8\
	-1	40	0	5	0	1	-1
		62	0	4	0	0	-5
	14	7	1			0	0	2
	8	2	0			0	1
	-1	42	0			1	0
		72	0			0	0

В индексной строке последней симплексной таблицы все оценки свободных переменных положительны. Следовательно, план оптимален.

Ответ: Z=72 в (7, 0, 0, 42, 2).