Планарность
Граф Gназываетсяпланарным, если его можно изобразить на плоскости без пересечения ребер.
П
Рис. 18
Рис. 19 
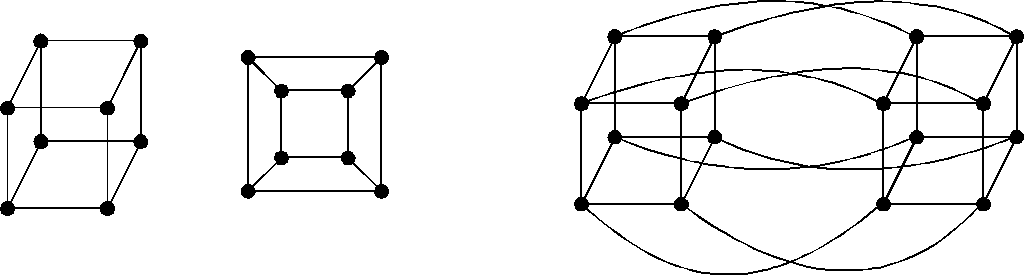
П
Рис. 20
Рис. 21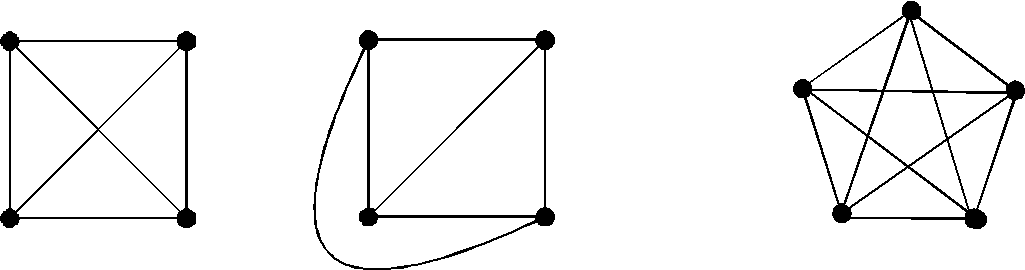
Т
Рис. 22 
![]() ,
где
,
где![]() –
количество вершин,
–
количество вершин,![]() –
граней,
–
граней,![]() –
ребер.
–
ребер.
Доказательство.
проведем индукцией по числу ребер.
При![]()
![]() ,
,![]() (океан),
и равенство
(океан),
и равенство![]() выполняется.
выполняется.
П
Рис. 23
![]() .
Возьмем произвольно реброе графаG, и удалим его, если оно висячее, то
вместе с соответствующей вершиной. Если
ребро было висячим, то для нового графаG' имеем
.
Возьмем произвольно реброе графаG, и удалим его, если оно висячее, то
вместе с соответствующей вершиной. Если
ребро было висячим, то для нового графаG' имеем ![]() ,
,![]() ,
,![]() (рис. 23а). Так как число ребер уG'
меньше, чем уG, то по индукционному
предположению
(рис. 23а). Так как число ребер уG'
меньше, чем уG, то по индукционному
предположению![]() и, следовательно,
и, следовательно,![]() .
.
Если
было удалено не висячее ребро (рис. 23б),
то
![]() ,
,![]() ,
,![]() .
Аналогично,
.
Аналогично,![]() и, следовательно,
и, следовательно,![]() .
Теорема доказана.
.
Теорема доказана.
Пусть G– планарный граф. Построим графG* следующим образом. Число вершин графаG* равно числу гранейG. Каждой граниG поставим в соответствие вершинуG*. Вершины вG* смежны тогда и только тогда, когда соответствующие им грани вGграничат по ребру, причем две вершиныG* соединяет столько ребер, сколько общих граничных ребер у соответствующих им граней. ГрафG* называетсядвойственным(сопряженным) графуG.
В
а)
б)
Рис. 24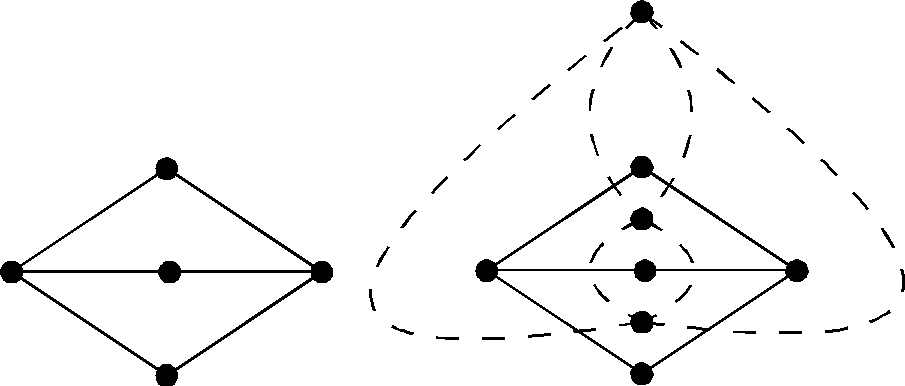
![]() ,
соединим ребрами
,
соединим ребрами![]() ,
пересекающими
,
пересекающими![]() .
Ребра
.
Ребра![]() графаGи
графаGи![]() графаG* ,
графаG* ,![]() ,
называютсяперпендикулярными(рис. 24б).
,
называютсяперпендикулярными(рис. 24б).
При
этом внутри каждой грани графа G*
лежит единственная вершина графаG.
Действительно, предположим, что внутри
некоторой грани![]() графаG* находятся несколько вершин
графаG* находятся несколько вершин![]() графаG. Так как из каждой вершины
выходит по крайней мере одно ребро, а
каждое ребро
графаG. Так как из каждой вершины
выходит по крайней мере одно ребро, а
каждое ребро![]() пересекает ровно одно ребро графаG,
то
пересекает ровно одно ребро графаG,
то![]() ,
гдеп– число ребер грани
,
гдеп– число ребер грани![]() .
Тогда, если какие-либо две из вершин
соединены ребром, то внутри грани
.
Тогда, если какие-либо две из вершин
соединены ребром, то внутри грани![]() найдется ребро
найдется ребро![]() ,
пересекающее это ребро, чего быть не
может, так как внутри грани ребер нет.
Пусть никакие две из вершин графаG,
находящиеся внутри
,
пересекающее это ребро, чего быть не
может, так как внутри грани ребер нет.
Пусть никакие две из вершин графаG,
находящиеся внутри![]() ,
не соединены ребром. Тогда все ребра,
выходящие из этих вершин, пересекают
ребра грани
,
не соединены ребром. Тогда все ребра,
выходящие из этих вершин, пересекают
ребра грани![]() .
Так как каждое ребро графа
.
Так как каждое ребро графа![]() пересекает ровно одно ребро графаG,
то
пересекает ровно одно ребро графаG,
то![]() ,
гдеп– количество ребер и,
соответственно, вершин грани
,
гдеп– количество ребер и,
соответственно, вершин грани![]() .
Проведение первого ребра из каждой
вершины не меняет число компонент
связности плоской области, ограниченной
гранью, проведение каждого следующего,
начиная со второго увеличивает число
компонент связности на 1. Таким образом,
в результате проведения всех ребер из
вершин
.
Проведение первого ребра из каждой
вершины не меняет число компонент
связности плоской области, ограниченной
гранью, проведение каждого следующего,
начиная со второго увеличивает число
компонент связности на 1. Таким образом,
в результате проведения всех ребер из
вершин![]() ,
число компонент связности области,
ограниченной гранью, не превышает
,
число компонент связности области,
ограниченной гранью, не превышает![]() .
Так как количество вершин грани
.
Так как количество вершин грани![]() равноп, то найдутся две вершины,
лежащие в одной компоненте связности.
Но тогда они принадлежат одной грани
графаG, что противоречит определению
сопряженного графа.
равноп, то найдутся две вершины,
лежащие в одной компоненте связности.
Но тогда они принадлежат одной грани
графаG, что противоречит определению
сопряженного графа.
Таким образом, существует взаимно-однозначное соответствие между гранями Gи вершинамиG*, вершинамиGи гранямиG*, ребрамиGиG*.
Рассмотрим теперь проблему планарности графов.
Теорема. Полный граф K5 не планарный.
Д
Рис. 25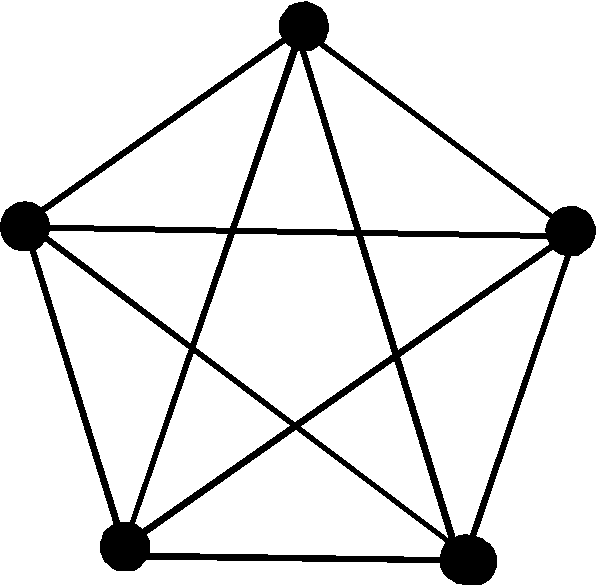
![]() .
Если бы он был планарный, то выполнялось
бы равенство
.
Если бы он был планарный, то выполнялось
бы равенство![]() ,
т.е.
,
т.е.![]() .
Двухугольные грани, очевидно, отсутствуют.
Имеем
.
Двухугольные грани, очевидно, отсутствуют.
Имеем![]() .
Кроме того,
.
Кроме того,![]() .
Умножим первое равенство на 3 и отнимем
из второго. Получим
.
Умножим первое равенство на 3 и отнимем
из второго. Получим![]() .
Получили противоречие, следовательно,
графK5 не планарный.
.
Получили противоречие, следовательно,
графK5 не планарный.
Теорема. Полный двудольный граф K3,3 не планарный.
Д
Рис. 26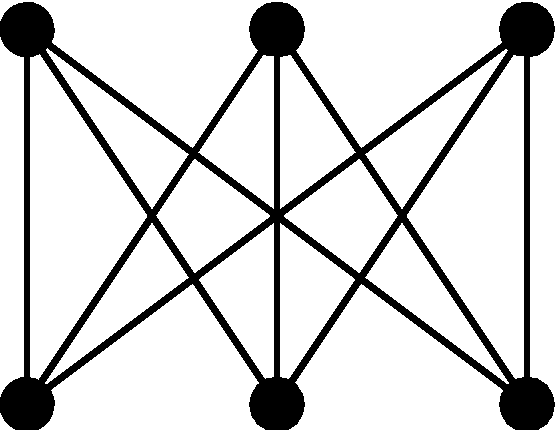
![]() .
Если бы он был планарный, то выполнялось
бы равенство
.
Если бы он был планарный, то выполнялось
бы равенство![]() ,
т.е.
,
т.е.![]() .
.
Имеем
![]() .
В силу того, что общее количество ребер
9, в графе не может быть граней с большим,
чем 9, числом ребер. Получаем
.
В силу того, что общее количество ребер
9, в графе не может быть граней с большим,
чем 9, числом ребер. Получаем![]() ,
,![]() .
Так как граф K3,3 двудольный,
то по критерию бихроматичности в нем
нет циклов нечетной длины, следовательно,
нет граней с нечетным числом ребер:
.
Так как граф K3,3 двудольный,
то по критерию бихроматичности в нем
нет циклов нечетной длины, следовательно,
нет граней с нечетным числом ребер:![]() .
Имеем
.
Имеем![]() ,
,![]() .
Умножив первое равенство на 4 и вычтя
его из второго, получим
.
Умножив первое равенство на 4 и вычтя
его из второго, получим![]() .
Противоречие, граф K3,3 не
планарный.
.
Противоречие, граф K3,3 не
планарный.
П
Рис. 27
Рис. 28
![]() и
и![]() (рис. 27).
(рис. 27).
Графы G1иG2называютсягомеоморфными, если существуют изоморфные графыG1' иG2', полученные из графовG1иG2 применением один или несколько раз операции разбиения ребер.
Пример. Графы на рис. 28 не изоморфны, но гомеоморфны.
Если граф содержит непланарный подграф, то он сам не планарен.
Теорема (Критерий планарности А.С. Понтрягина – К. Куратовского).ГрафGпланарный тогда и только тогда, когда у него нет подграфов, гомеоморфныхK5 илиK3,3.
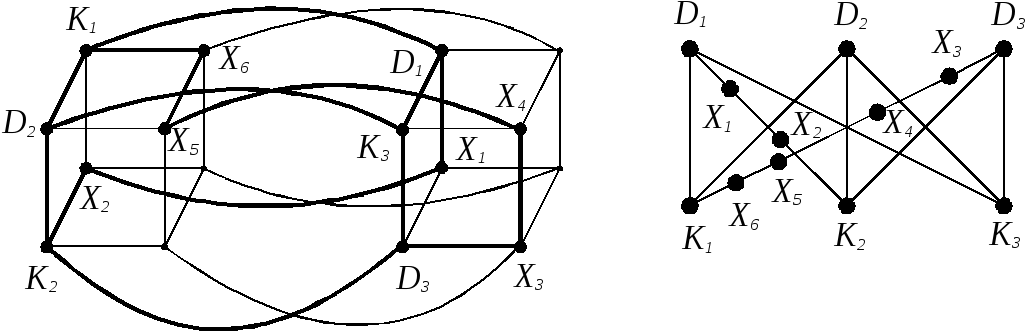
Пример. Доказать, что четырехмерный кубВ4не планарен.
Р
а)
б)
Рис. 29
X3
X4
X2