Степень вершины

Число ребер, инцидентных некоторой вершине v, называетсястепеньювершины и обозначается degv. В полном графеК_пстепень каждой вершины равна п– 1. максимальная и минимальная степени вершин графаGобозначаются символами(G) и(G) соответственно:

.

Вершина степени 0 называется изолированной, вершина степени 1 –концевой(висячей). Ребро, инцидентное концевой вершине, также называетсяконцевым. Вершина графа, смежная с каждой другой его вершиной, называетсядоминирующей.

Пример 2. В графеН₃ на рис 11 вершина 3 – висячая, вершина 2 – доминирующая,.

Пути в графах

Чередующаяся последовательность

(1)

вершин и ребер графа, такая что (i = 1, 2, …,l), называетсяпутем, соединяющим вершины и(или (, )-путем). Очевидно, что путь можно задать последовательностью

его вершин, а также последовательностью его ребер

.

Г

Рис. 14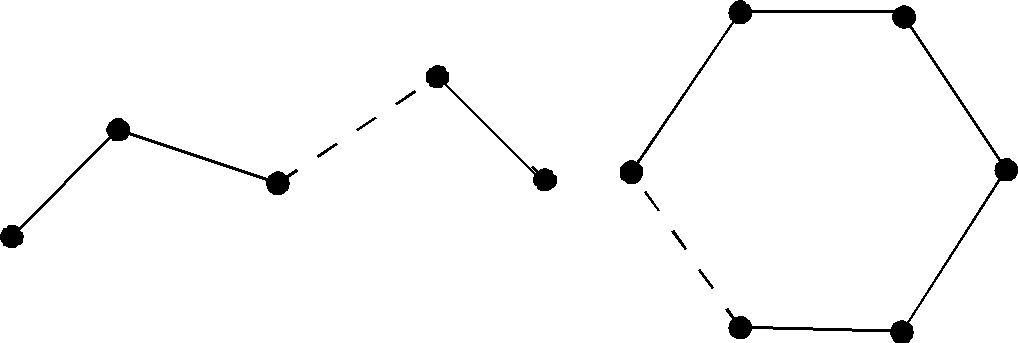

раф называетсясвязным, если любые две несовпадающие вершины в нем соединены маршрутом.

Путь называется простым, если все его вершины, кроме, может быть, крайних, различны. Путь называетсяцепью, если все его ребра различны, ипростой цепью, если все его вершины различны. Путь (2.1) называется циклическим, если. Циклическая цепь называетсяциклом, а циклическая простой путь –простым циклом. Простую цепь, имеющуюпвершин, будем обозначатьC_n, простой цикл –Z_n( рис.14).

Число lребер в пути (1) называется егодлиной.

Пример 3. В графеGна рис 11 (1, 4, 5, 2, 4) – цепь; (1, 4, 5, 2, 3) – простая цепь; (1, 4, 5, 2, 4, 1) – циклический путь, не являющийся циклом; (4, 3, 2, 4) – цикл.

Метрические характеристики графа

Пусть G– граф, аи иv– две его несовпадающие вершины. Длина кратчайшего (и,v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинамиииv и обозначается черезd(u,v). Положим ещеd(u,и) = 0. Очевидно, что введенное таким образом расстояние удовлетворяетаксиомам метрики:

1. d(u, v)  0,

2. d(u,v) = 0 тогда и только тогда, когдаu = v,

3. d(u, v) = d(v, u),

4. d(u,v) +d(v,w)d(u,w) (неравенство треугольника).

Для фиксированной вершины ивеличина

называется эксцентриситетом вершины и. Максимальный из всех эксцентриситетов вершин графа называетсядиаметром графаGи обозначается черезd(G). Тем самым,

.

В

2

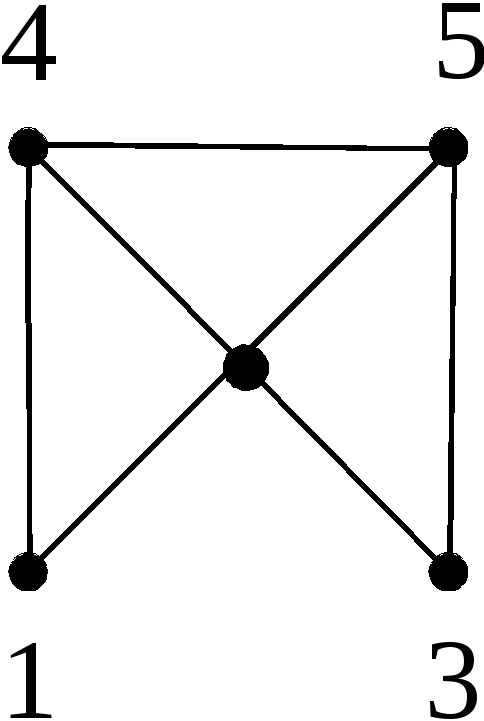
Рис. 15

ершинаvназываетсяпериферийной, если.

Простая цепь длины d(G), расстояние между концами которой равноd(G), называетсядиаметральной цепью.

Пример 4. В графе на рис. 15d(1,2) = 1,d(1, 3) = 2;е(1) = 2;d(G) = 2. Все вершины, кроме вершины 2 являются периферийными, (1, 2, 3) – диаметральная цепь.

Минимальный из эксцентриситетов вершин связного графа называется его радиусоми обозначаетсяr(G):.

Очевидно, что радиус графа не больше его диаметра.

Вершина называется центральной, если. Множество всех центральных вершин графа называется егоцентром. Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин.

Способы задания графов

Существует несколько способов задания графа:

1. графический;

2. с помощью перечисления ребер;

3. с помощью матрицы смежности;

4. с помощью матрицы инцидентности.

С графическим способом, при котором вершины графа изображаются точками на плоскости или в пространстве, а ребра – непрерывными кривыми, соединяющими соответствующие точки, мы уже фактически познакомились. При этом один и тот же граф можно представлять по-разному, с пересечением ребер или без (рис. 5).

Теорема. Вможно изобразить любой конечный граф так, чтобы не было пересечений ребер во внутренних точках.

Д

Рис. 16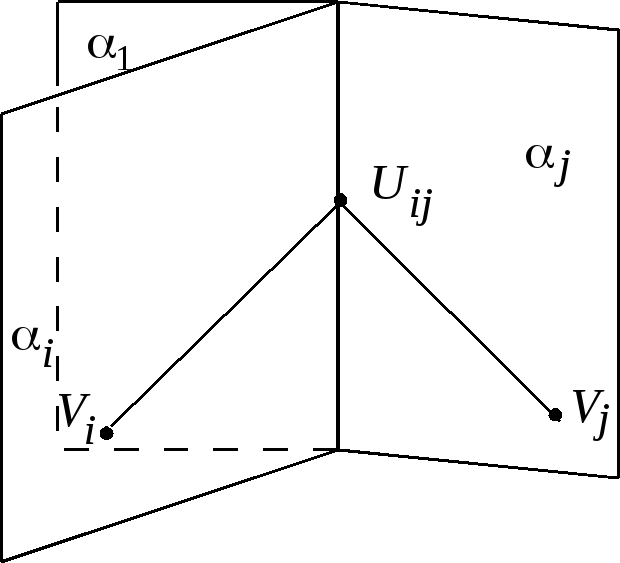

оказательство. ПустьG– произвольный граф с множеством вершинV(G) и множеством реберE(G). Занумеруем множество вершин:V(G) = {v₁,v₂, …,v_n}. Тогда каждому ребруесоответствует пара инцидентных ему вершин (v_i,v_j), гдеi < jn. Проведем в пространстве произвольную прямуюlип различных полуплоскостей₁,₂, …,_п, границей которых является прямаяl(рис. 16). На каждой плоскости_iвозьмем произвольно точкуV_i, не принадлежащую прямойl, а на прямойl – произвольные различные точкиU_ij, соответствующие ребрам (v_i,v_j). Изображением вершиныv_iграфаG будет служить точкаV_i, изображением ребра (v_i,v_j) – ломанаяV_i U_ij V_j. Очевидно, при этом ломаные, соответствующие разным ребрам, могут пересекаться только в точках, соответствующих вершинам. Теорема доказана.

В памяти ЭВМ граф часто задается перечислением ребер. Например, для графа, изображенного на рис. 17: (1, 2), (2, 3), (2, 4).

Р

Рис. 17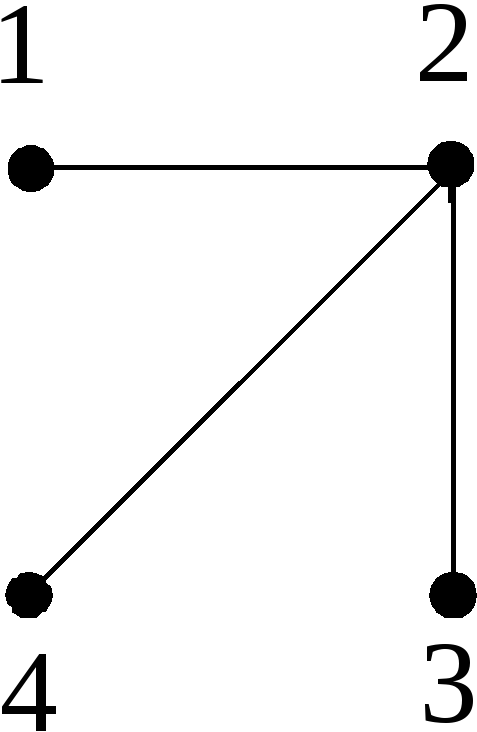

ассмотримспособы задания графов с помощью матриц..ПустьG– граф порядкап. Занумеруем его вершины:. Определим матрицуА = А(G) размерапп следующим образом:

А(G) называетсяматрицейсмежностиграфаG.

Если граф Gбез петель, тоа_ii 0. Если в графеG допускаются кратные ребра, тоа_ijравно количеству ребер, соединяющих вершиныа_i иа_j . Для неориентированного графа матрицаА(G) является симметрической, для ориентированного – нет.

Абстрактный граф приводит к различным матрицам смежности в зависимости от нумерации вершин. Посмотрим, как связаны между собой эти матрицы. Пусть GиН – помеченные графы порядкапи . Это означает, чтоGиНразличаются только нумерацией вершин, т.е. существует подстановкаsна множестве вершин, сохраняющая смежность: вершиныииvтогда и только тогда смежны вG, когда их образы s(и) иs(v) смежны вН. ПоложивА(G) =А,В(G) =В, получаем:

Следовательно, графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов. Из этого вытекает, что ранги матриц изоморфных графов равны, что позволяет ввести для абстрактного графа следующее определение ранга: рангом графаназывается ранг его матрицы смежности. Как и в случае матриц, ранг графаG будем обозначать через rankG.

Теорема. Для каждого связного графаGверно неравенство.

Доказательство.Пусть. Рассмотрим матрицу смежностиА(G), причем выберем нумерацию вершин так, чтобы вершины одной из диаметральных цепей имели номера 1, 2, …,d+1:– диаметральная цепь. Очевидно, чтоявляется клеточной матрицей, в левом верхнем углу которой расположена матрица смежностиАпорожденного подграфаЭтот подграф является

простой цепью, следовательно,

– симметрическая матрица порядка d+ 1, все элементы которой, за исключением двух ближайших к диагонали полос единиц, равны нулю. минор порядкаd матрицыА, остающийся после вычеркивания первого столбца и последней строки, равен 1. Следовательно,. Теорема доказана.

Выведем необходимое условие изоморфности графов. Пусть s– произвольная подстановка, действующая на множестве {1, 2, …,n}. Определим матрицуS размерностиn n, положив

Очевидно, что в каждой строке и в каждом столбце матрицы Sсодержится ровно по одной единице и. С помощью прямых вычислений проверяется, что

Таким образом, . Из этого следует, что матрицы смежности изоморфных графов подобны. Поэтому равны характеристические многочлены этих матриц. Следовательно, корректно определениехарактеристического многочлена графа, как характеристического многочлена его матрицы смежности. Спектр матрицы смежности, т.е. совокупность корней характеристического многочлена с учетом их кратности, называетсяспектром графа. Следует заметить, что из совпадения характеристических многочленов графов не следует их изоморфизма.

Определим матрицу инцидентности графа. Пусть -граф,. Определим матрицуI=I(G) размерап т,положив

Матрица I называетсяматрицей инцидентностиграфаG. В каждом ее столбце ровно две единицы, одинаковых столбцов нет.

Для ориентированных графов определение матрицы инцидентности Iвидоизменяется:

Теорема. Графы (ориентированные графы) изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга перестановками строк и столбцов.