Изоморфизм графов

Легко подсчитать число графов с фиксированным множеством вершин V. Эти графы различаются своими ребрами, и поэтому их число равно количеству подмножеств множестваVV, т.е., гдеп= | V |. Однако эти графы на всегда следует различать. Как в применении теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа) и связи между объектами (ребра графа). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать. Такие графы называютсяизоморфными.

Пусть GиН– графы, а– биекция. Если для любых вершинииvграфаG их образыисмежны вН тогда и только тогда, когдаииvсмежны вG, то эта биекция называетсяизоморфизмом графа G на граф Н. Если такой изоморфизм существует, то мы пишем и говорим, что графыGиН изоморфны.

П

Рис. 9

Рис. 8

ример 1.Графы, представленные на рис. 8 изоморфны, указана соответствующая изоморфизмам нумерация вершин. Графы на рис. 9 неизоморфны (например, вследствие того, что в первом графе есть циклы из трех ребер, а во втором их нет).

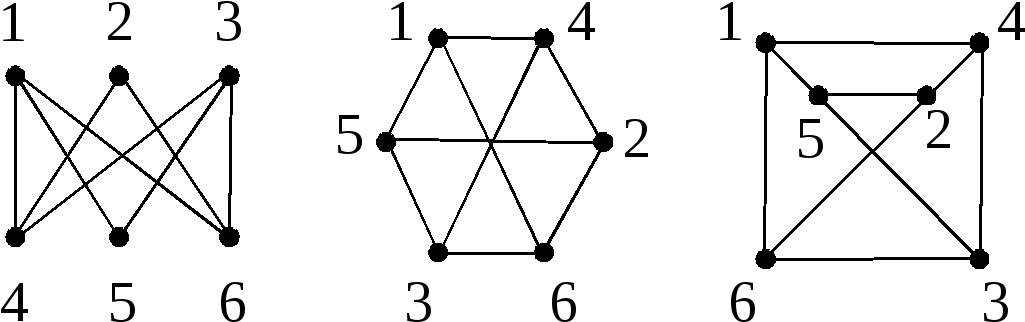
Очевидно, что отношение изоморфизма графов является эквивалентностью, т.е. оно симметрично, рефлексивно и транзитивно. Следовательно, все графы разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игнорируется при введении понятия графа. Класс изоморфных графов принято называть абстрактным графом.

В

Рис. 10.

некоторых случаях приходится различать изоморфные графы. Граф порядкапназываетсяпомеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2, …,п. Отождествив каждую из вершин графа с ее номером (а, следовательно, множество вершин – с множеством чисел {1, 2, …,п}), определим равенство графовGиНодного и того же порядка:G=Нтогда, когдаЕG=ЕН. На рис. 10 изображены три разных помеченных графа.

Число g_nпомеченных графов порядкапопределяется сложно. Известнаформула Пойа

,

дающая асимптотику числа g_n. Эта формула означает, что две функцииg(п)=g_n иf(n)=асимптотически равны, т.е..

Операции над графами

Граф Нназываетсяподграфом(иличастью) графаG, еслиVHVG,ЕHЕG. ПодграфНназываетсяостовным подграфом, еслиVH=VG. Если множество вершин подграфаНестьU, а множество его ребер совпадает с множеством всех ребер графаG, оба конца которых принадлежатU, тоНназываетсяподграфом, порожденным множеством U. На рис.11 изображены графGи три его подграфаН₁,Н₂иН₃ , среди которыхН₃ является остовным, аН₂– порожденным.

Г

Рис. 11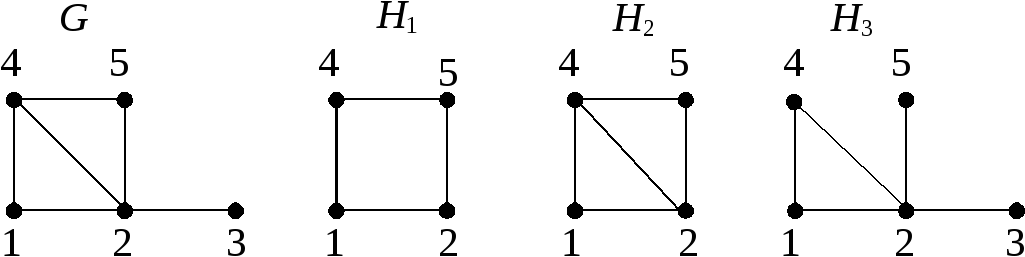

рафНназываетсяобъединениемграфовFиG, еслиV(H) =V(G) V(F) иE(H)=E(G) E(F). В этой ситуации пишутН=FG. ОбъединениеFG называетсядизъюнктным, еслиV(G) V(F) =.

В

Рис. 12

ведем операцию произведения графов. Пусть задано два графаG₁ = (V₁,E₁),G₂ = (V₂,E₂).Произведением графовназывается граф, для которого– декартово произведение множеств вершин исходных графов, аE(G) определяется следующим образом: вершины (и₁,и₂) и (v₁,v₂) в графеGсмежны тогда и только тогда, когда илии₁=v₁, аи₂ иv₂ смежны вG₂, илии₂=v₂, аи₂ иv₂ смежны вG₁(рис. 12).

Очевидно, что ,

.

С помощью операции произведения можно определить п-мерный кубрекуррентно:.

Покажем, что это определение совпадает с данным ранее. Действительно, . Вершины графаможно представить векторами длиныпиз 0 и 1 таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются в одной координате.

Д

Рис. 13

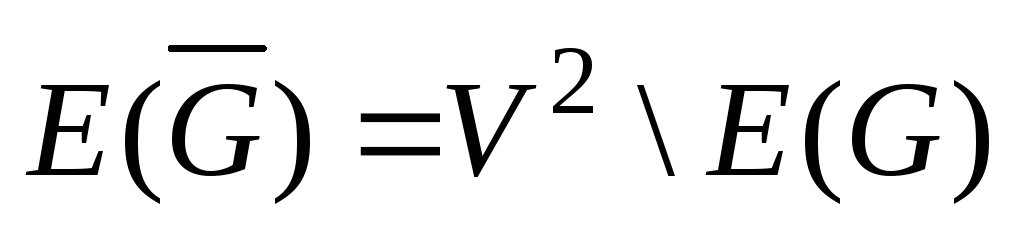ля произвольного графаG следующим образом определяетсядополнительный граф (илидополнение):, и две несовпадающие вершины смежны втогда и только тогда, когда они не смежны вG:(рис. 13).

Граф, изоморфный своему дополнению, называется самодополнительным.