Явление Гиббса.

Перейдем к рассмотрению одного из наиболее важных с практической точки зрения результатов теории рядов Фурье, который называется явлением Гиббса. Известно, что, в точках непрерывности ряд Фурье сходится к значению функции, а в точке разрыва к среднему двух граничных значений. Каждый член ряда представляет собой непрерывную функцию и, следовательно, теорема о том, что равномерно сходящийся ряд из непрерывных функций сходится к непрерывной функции, указывает теперь на то, что в точке разрыва сходимость ряда Фурье носит особый характер.

Для практических целей всегда приходится ограничивать любой формируемый ряд Фурье. Это усечение приводит к явлению, которое называется явлением Гиббса. Наиболее наглядно этот эффект можно продемонстрировать на примере прямоугольной волны.

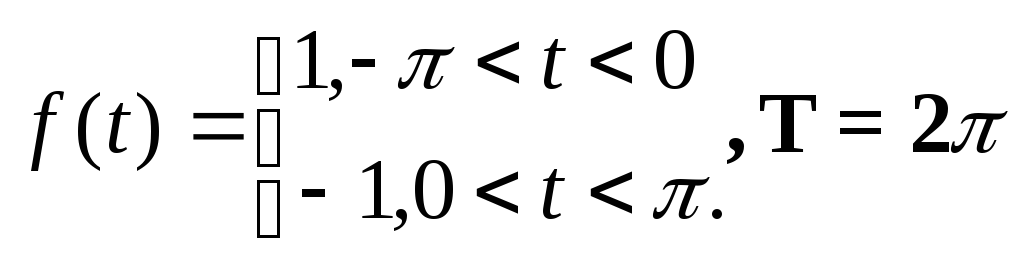
Решение:

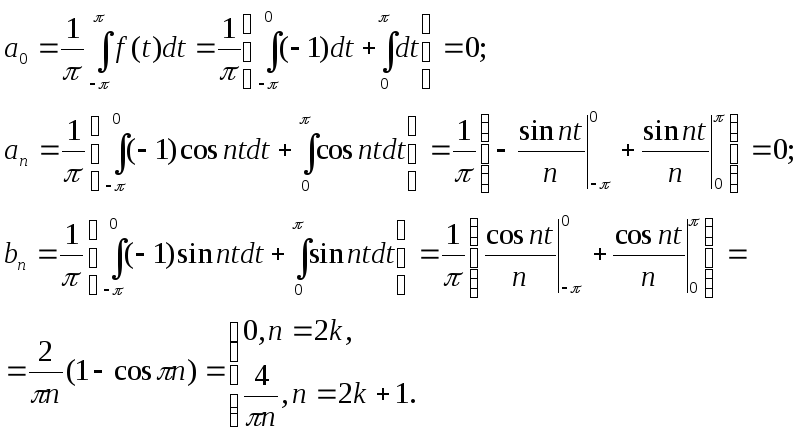
Получаем искомое разложение

В силу симметрии волны можно рассмотреть только сходимость различных сумм, на участке [0,] к значению f(t)=1. Если построить графики частичных сумм, то можно видеть, что они имеют колебательный характер относительно прямой f(t)=1. Наибольшую амплитуду при этом имеет первый максимум после точки разрыва x=0 и последний максимум перед точкой разрыва x=(кривая частичной суммы симметрична относительно x=/2).Если выделить точки разрыва 0 ималыми- окрестностями, то в оставшемся промежутке [,-] ряд сходится равномерно. Иными словами на этом промежутке с ростом n амплитуды осцилляций уменьшается и при достаточно больших n графики частичных сумм сколь угодно тесно примыкают к прямой y=1. Вблизи же точек разрыва x=0,, где функция скачком переходит от значения 1 к значению 0, равномерность приближения нарушается. Однако, прежде чем устремиться к значению 0, графики частичных сумм продолжают колебаться около прямой y=1 с возрастающей с увеличением n частотой. При этом, амплитуда этих колебаний вовсе не имеет тенденции бесконечно уменьшаться при n, а остается практически постоянной. Этот дефект сходимости и носит название явления Гиббса.

Чтобы увидеть пути устранения этого эффекта рассмотрим математически, к чему ведет усечение ряда Фурье.

Пусть функция f(t) задана в виде комплексного ряда Фурье

Процесс усечения этого ряда до конечной суммы

есть то же самое, что умножение коэффициентов разложения с на числа …0,0,0,1,1,1,1,……0,0,0,……(2N+1) значение равно единице, остальные значения равны нулю. Сформируем из этих чисел последовательность d:

Функцию, имеющую коэффициенты Фурье d_nможно получить, просуммировав соответствующий ряд Фурье.

Таким образом, с помощью коэффициентов d_nусеченный ряд Фурье для функции f(t) можно представить в виде бесконечного ряда, но для функции, коэффициенты Фурье которой есть с_nd_n. такой функцией является свертка функций f(t) и h(t),т.е.

Таким образом, усеченный ряд Фурье для f(t) эквивалентен ее свертыванию с

При этом функцию h(t) называют свертывающим окном. Т.к. при больших N h(t) быстроколеблющаяся функция с максимальным значением (2N+1) в нуле и резко спадающая в обе стороны от нуля, то при свертке с прямоугольным импульсом возникают осцилляции, составляющие явление Гиббса. Эта неравномерная сходимость (явление Гиббса) может быть уменьшена путем использования менее резкого усечения рядов Фурье с помощьюокон данных различной модификации. Например:

Окно Бартлета: (N,n)=1-n/N, 0<n<N

Окно Ханнинга: (N,n)=1/2[1-cos((n-N)/N)], 0<n<N

Окно Хамминга: (N,n)= 0.54- 0.46cos((n-N)/N), o<n<N

И т. д.

Приближенное выражение для искомой функции будет даваться частичной суммой ряда:

Список литературы:

1. Я.С. Бугров, С.М. Никольский ”Дифференциальные уравнения. Кратные интегралы. Ряды.”

2. В.А. Ильин, Э.Г. Позняк “Основы мат анализа ч2”

3. П.И. Романовский “Ряды Фурье” М. Наука 1980 г.

4. Г.П. Толсктов “Ряды Фурье” М. Наука 1980 г.

5. Р.В. Хемминг “Цифровые фильтры” М. Советское радио 10980 г.