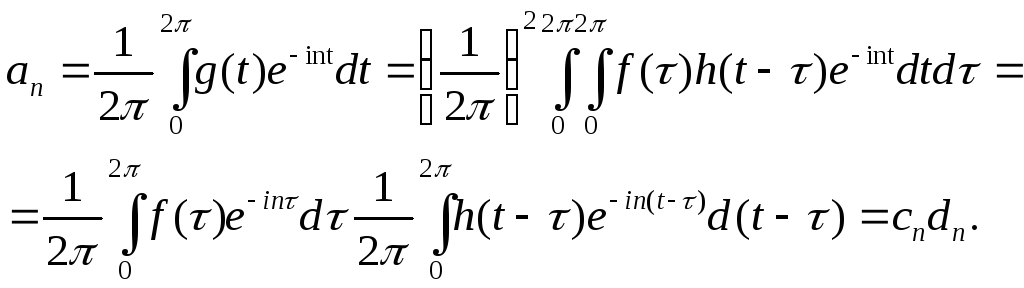Коэффициенты Фурье

Допустим, что функция f(x) периода 2разложена в тригонометрический ряд

(1) и оказалось, что этот ряд равномерно сходится к ней.

Каждый член ряда (1) есть непрерывная функция, и ,так как ряд (1) по условию равномерно сходится, то его сумма f(x) есть непрерывная функция.

Помножим левую и правую части (1) на cos mx, где m- натуральное число. Так как функция cos mx непрерывна и ограничена, то полученный ряд снова будет состоять из непрерывных функций и снова будет равномерно сходиться, теперь уже к непрерывной функции f(x)cos mx. Но равномерно сходящиеся ряды непрерывных функций законно интегрировать почленно на конечном отрезке. Проинтегрируем полученный ряд почленно на периоде, т.е. на отрезке [-,]:

Второе равенство следует из ортогональности тригонометрических функций и формул (2) п.4

Аналогично получим

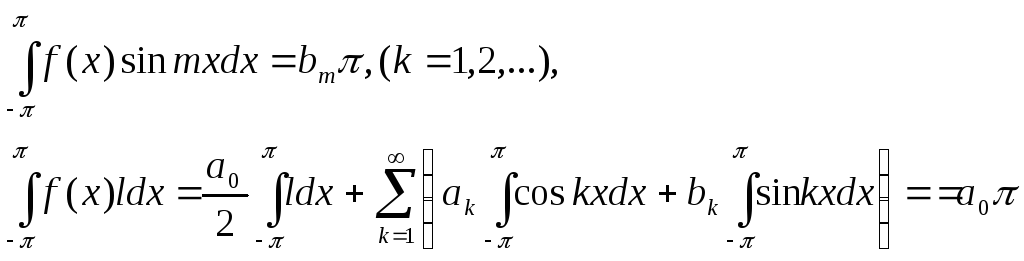
В силу последних трех формул (2) п.4. (Орт. Св-ва)

Итак, мы доказали что если функция f представима в виде суммы тригонометрического ряда (1), равномерно сходящегося ( для всех x!), то числа а_k , b_k необходимо являются коэффициентами Фурье функции f.

Таким образом, всякий равномерно сходящийся тригонометрический ряд является рядом Фурье своей суммы.

Комплексная форма ряда Фурье.

Пусть a_kи b_k –коэффициенты Фурье функции f(x). На основании формул Эйлера

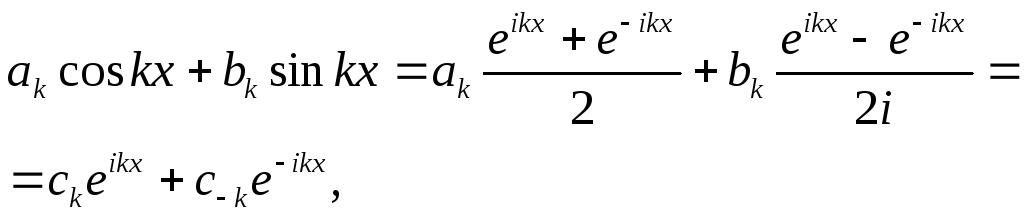
где (будем считать b₀=0)

(1) Отсюда

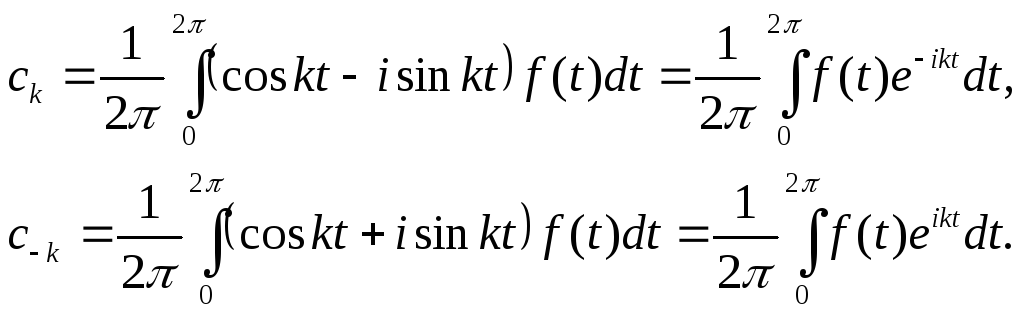
Эти два равенства можно записать в виде единой формулы

(2) Важно заметить, что если f(x)– действительная функция, то а_kи b_k действительны, а числа с_kи с_-k, хотя вообще и комплексны, но взаимно сопряжены:

(3) Очевидно, n-я сумма ряда Фурье функции f может быть записана в виде

(4) А сам ряд Фурье функции f- в виде ряда

(5) Мы будем говорить, что ряд (5) сходится для данного значения x , если существует предел

Таким образом определенная сходимость называется сходимостью в смысле главного значения.

Ведь можно было бы считать его сходящимся, если существует предел

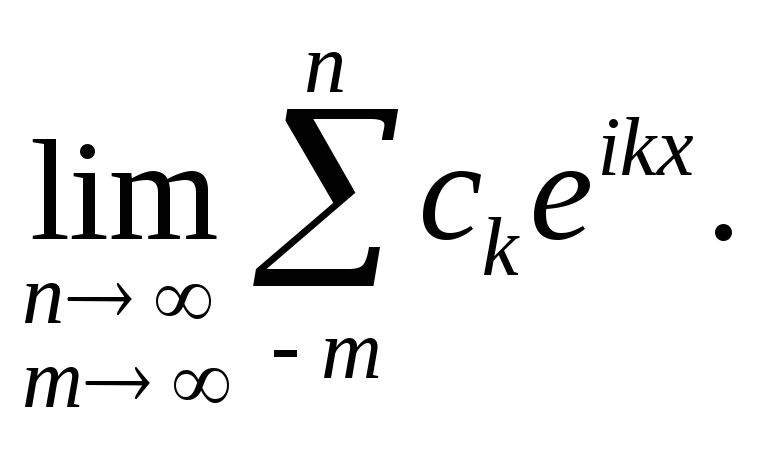
,когда и n неограниченно возрастают независимо друг от друга.

Комплексные функции образуют ортогональную систему на отрезке [0,2],так как при kl

Далее

Рассмотрим вопрос сложения и умножения функций, представленных в виде ряда Фурье.

Пусть

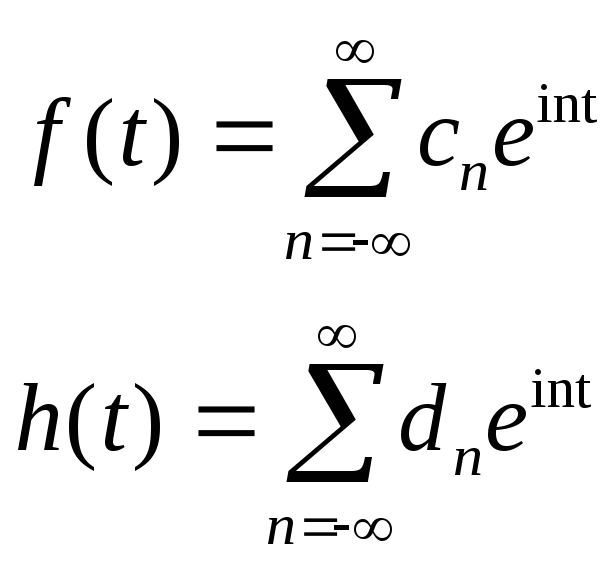
Очевидно, разложение в ряд Фурье линейной комбинации функций сводится к нахождению линейной комбинации соответствующих коэффициентов Фурье.

Найдем разложение в ряд Фурье произведения функций f(t) и h(t).

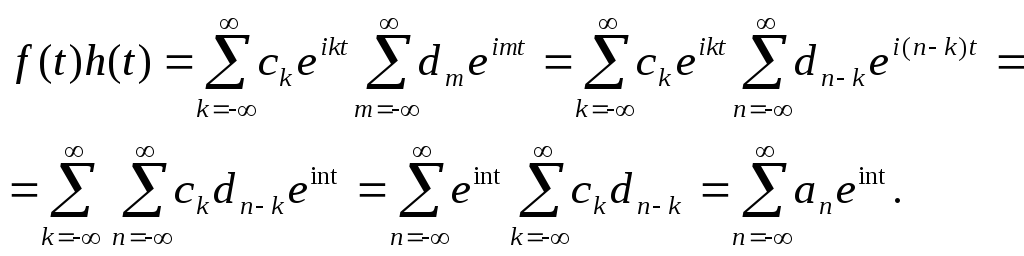
При этом мы ввели замену n=k+m и переставили местами суммирования по индексам n и k. Таким образом, n-й коэффициент разложения произведения двух функций будет иметь вид

Это выражение называется сверткой последовательностей {c_k} и {d_k}.

Таким образом, чтобы получить коэффициенты разложения произведения, нужно вычислить свертки коэффициентов.

Решим теперь обратную задачу. Найдем функцию, коэффициенты Фурье которой равны произведению соответствующих коэффициентов из двух разложений, т.е. функцию, которой соответствует ряд Фурье

Покажем, что эта функция есть свертка периодических функций f(t) и h(t) , определяемая следующим образом:

Вычислим коэффициенты Фурье свертки.