МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ
Технический университет
Курсовая работа
по теме: «Исследование эффекта Гиббса при разложении
функций в ряд Фурье»
Выполнил: студент ЭКТ-32 Иванов А.С.
Преподаватель: Богданова Н.А.
Москва 2002
Теоретическая часть
1![]() .
Тригонометрические ряды.
.
Тригонометрические ряды.
Функция f(x) называется периодической (периода а), если она определена на всей действительной оси и для нее выполняется равенство f(x+a) =f(x) для всех x.
Например, тригонометрические функции
1,cosx,sinx,cos2x,sin2x,cos3x,… (1) имеют период 2.
На самом деле функции cos kx и sin kx для каждого натурального k имеют период 2k. Таким образом 2/k<2при k>1. Постоянная же y=1 имеет как угодно малый период. Однако все функции последовательности (1) имеют период 2.
Периодическая функция S=f(t) изображает периодическое движение (колебание) точки, имеющей в момент времени t координату s(на оси s).
Функция (периода 2l)
![]() ,
(2)где А>0, l>0 и-постоянные,
k-натуральное, определяетгармоническое
колебание точки самплитудой А,
фазой и частотой
k.
,
(2)где А>0, l>0 и-постоянные,
k-натуральное, определяетгармоническое
колебание точки самплитудой А,
фазой и частотой
k.
Функция (2) имеет период 2l/k, т.е. одно полное колебание происходит за промежуток времени 2l/k . Количество же колебаний в единицу времени k/2l. Именно число k/2l нужно было бы назвать частотой колебания, но обычно частотой (колебания) называют число k. Отметим, что функция
![]() ,
,
г![]() де
k- натуральное число, определяет
гармоническое колебание, потому что
де
k- натуральное число, определяет
гармоническое колебание, потому что
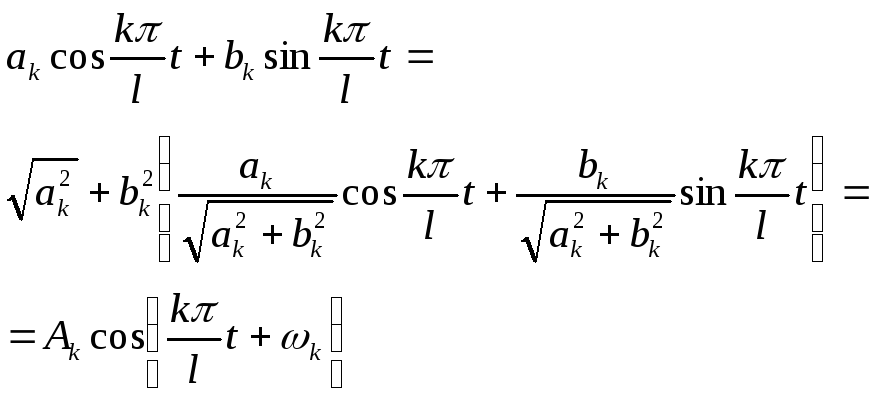
![]() где
где
а определяется однозначно из соотношений
![]()
Конечная сумма гармонических колебаний с данным периодом 2l представляет собой сложное колебание
![]() (3)Наконец,
более сложное периодическое колебание
можно получить как сумму сходящегося(
для всех t) ряда
(3)Наконец,
более сложное периодическое колебание
можно получить как сумму сходящегося(
для всех t) ряда
![]() ,
(4)
называемоготригонометрическим
рядом.
,
(4)
называемоготригонометрическим
рядом.
Числа akи bkназываютсякоэффициентами тригонометрического ряда (4),а отдельные его слагаемые
![]()
называются членами ряда (4) или егогармониками(соответствующими частоте k).
2. Ряд Фурье
Пусть задана функция f(t) периода 2l и известно, что ее можно разложить в тригонометрический ряд:
![]() (1)
Т.е. она
уже есть сумма некоторого тригонометрического
ряда для всех t . Спрашивается, как
определить по функции f(t) коэффициенты
ak, bk.
(1)
Т.е. она
уже есть сумма некоторого тригонометрического
ряда для всех t . Спрашивается, как
определить по функции f(t) коэффициенты
ak, bk.
Этот вопрос принципиально был решен математиками и физиками в начале прошлого столетия. Существенный вклад в его решение внес Ж. Фурье. Он показал, что коэффициенты ak,bkтригонометрического ряда, представляющего периодическую периода 2l функцию f(t), вычисляются по формулам
 (2)
Числа аkи bk, вычисляемые
по этим формулам, называюткоэффициентами
Фурье функции f(t), а тригонометрический
ряд (1), в который вместо аkи bkподставлены
соответствующие коэффициенты Фурье,
называютрядом Фурьефункции f(t).
(2)
Числа аkи bk, вычисляемые
по этим формулам, называюткоэффициентами
Фурье функции f(t), а тригонометрический
ряд (1), в который вместо аkи bkподставлены
соответствующие коэффициенты Фурье,
называютрядом Фурьефункции f(t).
Отметим, что если функция f(t) имеет период а и интегрируема на отрезке [0,a] или, как говорят, на периоде, то для нее справедливо равенство
![]() (3)
для любого
действительного числа.
(3)
для любого
действительного числа.
Свойство (3), в частности, показывает, что коэффициенты Фурье периодической функции f(t) периода 2l можно записать в виде
 ,
,
где – произвольное действительное число, потому что функции cos и sin периода 2l, а произведение функций периода 2l- в свою очередь функции периода 2l.
Отметим еще, что если функция f – четная на отрезке [-a, a], то
![]()
Если же функция f нечетная на отрезке [-a, a] , то
![]()
Функция cos четная, а sin – нечетная.
Кроме того, произведение двух четных и двух нечетных функций есть функция четная, а произведение четной функции на нечетную есть нечетная функция. Поэтому для четной периода 2l функции f(t)

А для нечетной –