Практическая часть Разложение функции в ряд Фурье.

Исходные данные:

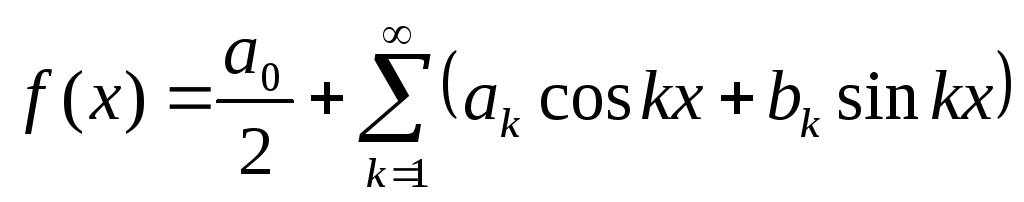
Найдем коэффициенты ряда:

,

,

,

Подставим коэффициенты в ряд Фурье 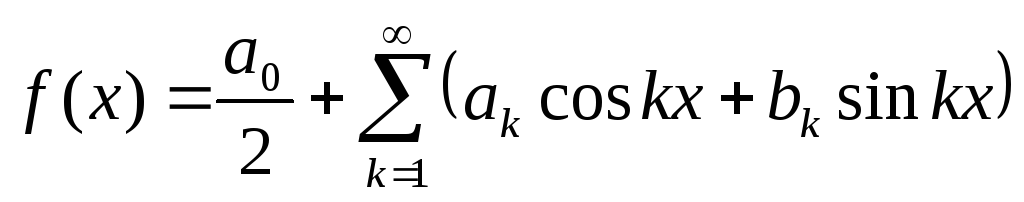и получим

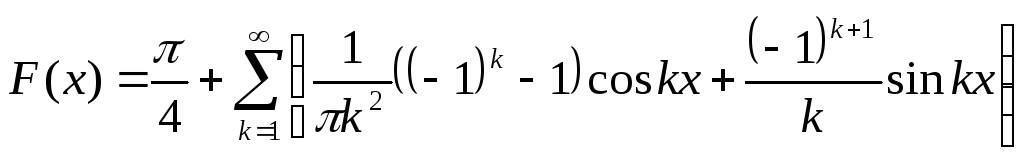
Текст программы (MathLab 6.0)

pi=acos(-1);

m=50;

x=[-pi:0.1:pi];

f=pi/4;

f1=pi/4;

f2=pi/4;

f3=pi/4;

for k=1:m,

ak=(1/(pi*k^2))*((-1)^k-1);

bk=((-1)^(k+1))/k;

f=f+(ak*cos(k*x)+bk*sin(k*x));

f1=f1+(ak*cos(k*x)+bk*sin(k*x))*(1-k/m);%окно Бартлера

f2=f2+(ak*cos(k*x)+bk*sin(k*x))*(1/2)*(1-cos(pi*(k-m)/m));%окно Ханнинга

f3=f3+(ak*cos(k*x)+bk*sin(k*x))*(0.54-0.46*cos(pi*(k-m)/m));%окно Хамминга

end

x1=[-pi:0.1:0];

y1=0;

x2=[0:0.1:pi];

y2=x2;

plot(x,f,'b',x1,y1,'+',x2,y2,'+');grid

%plot(x,f1,'b',x1,y1,'+',x2,y2,'+');grid %окно Бартлера

%plot(x,f2,'r',x1,y1,'+',x2,y2,'+');grid %окно Ханнинга

%plot(x,f3,'r',x1,y1,'+',x2,y2,'+');grid %окно Хамминга

%plot(x,f,x,f1,'b',x,f2,'r',x,f3,'g',x1,y1,'+',x2,y2,'*');grid

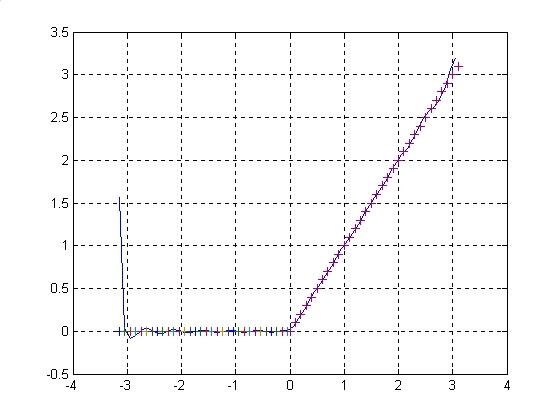
Графики

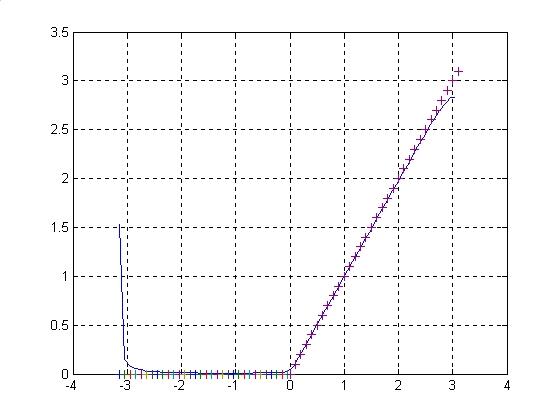
1.График функции и неусеченного ряда Фурье:

2.График функции и ряда Фурье, усеченного окном Бартлера:

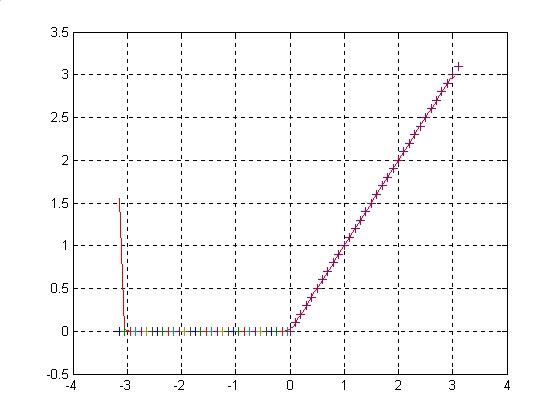
3. График функции и ряда Фурье, усеченного окном Хамминга:

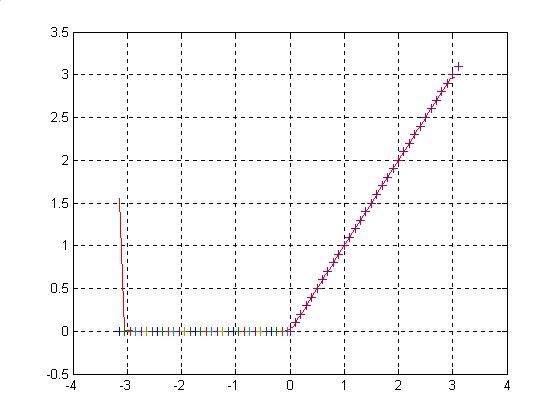
4. График функции и ряда Фурье, усеченного окном Ханнинга:

Список литературы:

1. Я.С. Бугров, С.М. Никольский ”Дифференциальные уравнения. Кратные интегралы. Ряды”

2. В.А. Ильин, Э.Г. Позняк “Основы математического анализа ч.2”

3. П.И. Романовский “Ряды Фурье” М. Наука 1980 г.

4. Г.П. Толсктов “Ряды Фурье” М. Наука 1980 г.

5. Р.В. Хемминг “Цифровые фильтры” М. Советское радио 1980 г.