5. Явление Гиббса.

Перейдем к рассмотрению одного из наиболее важных с практической точки зрения результатов теории рядов Фурье, который называется явлением Гиббса. Известно, что, в точках непрерывности ряд Фурье сходится к значению функции, а в точке разрыва к среднему двух граничных значений. Каждый член ряда представляет собой непрерывную функцию и, следовательно, теорема о том, что равномерно сходящийся ряд из непрерывных функций сходится к непрерывной функции, указывает теперь на то, что в точке разрыва сходимость ряда Фурье носит особый характер.

Для практических целей всегда приходится ограничивать любой формируемый ряд Фурье. Это усечение приводит к явлению, которое называется явлением Гиббса. Наиболее наглядно этот эффект можно продемонстрировать на примере прямоугольной волны.

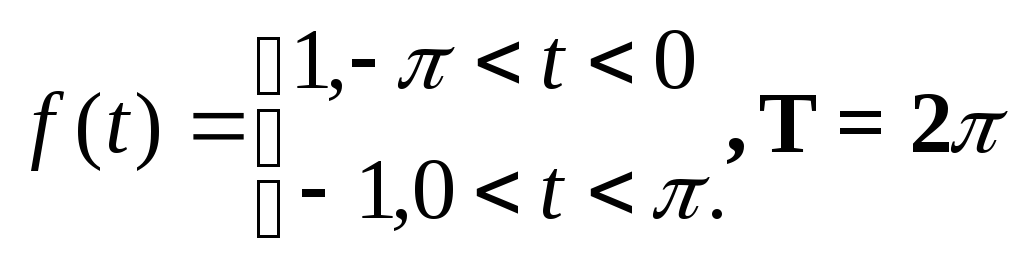
Решение:

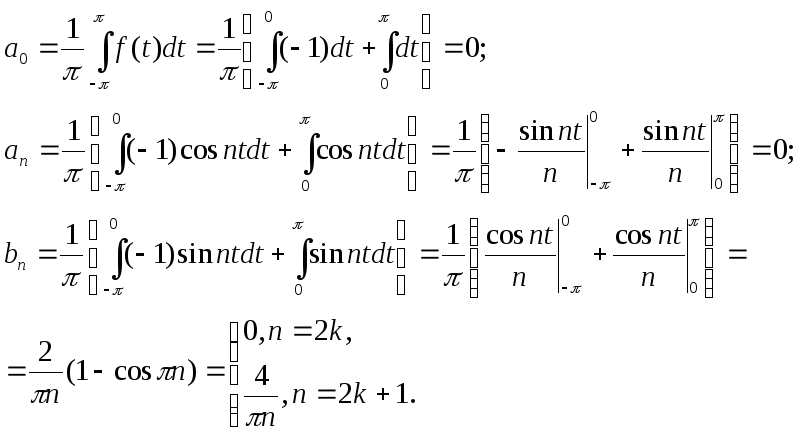
Получаем искомое разложение

В силу симметрии волны можно рассмотреть только сходимость различных сумм, на участке [0,] к значению f(t)=1. Если построить графики частичных сумм, то можно видеть, что они имеют колебательный характер относительно прямой f(t)=1. Наибольшую амплитуду при этом имеет первый максимум после точки разрыва x=0 и последний максимум перед точкой разрыва x=(кривая частичной суммы симметрична относительно x=/2).Если выделить точки разрыва 0 ималыми- окрестностями, то в оставшемся промежутке [,-] ряд сходится равномерно. Иными словами на этом промежутке с ростом n амплитуды осцилляций уменьшается и при достаточно больших n графики частичных сумм сколь угодно тесно примыкают к прямой y=1. Вблизи же точек разрыва x=0,, где функция скачком переходит от значения 1 к значению 0, равномерность приближения нарушается. Однако, прежде чем устремиться к значению 0, графики частичных сумм продолжают колебаться около прямой y=1 с возрастающей с увеличением n частотой. При этом, амплитуда этих колебаний вовсе не имеет тенденции бесконечно уменьшаться при n, а остается практически постоянной. Этот дефект сходимости и носит название явления Гиббса.

Чтобы увидеть пути устранения этого эффекта рассмотрим математически, к чему ведет усечение ряда Фурье.

Пусть функция f(t) задана в виде комплексного ряда Фурье

Процесс усечения этого ряда до конечной суммы

есть то же самое, что умножение коэффициентов разложения с на числа …0,0,0,1,1,1,1,……0,0,0,……(2N+1) значение равно единице, остальные значения равны нулю. Сформируем из этих чисел последовательность d:

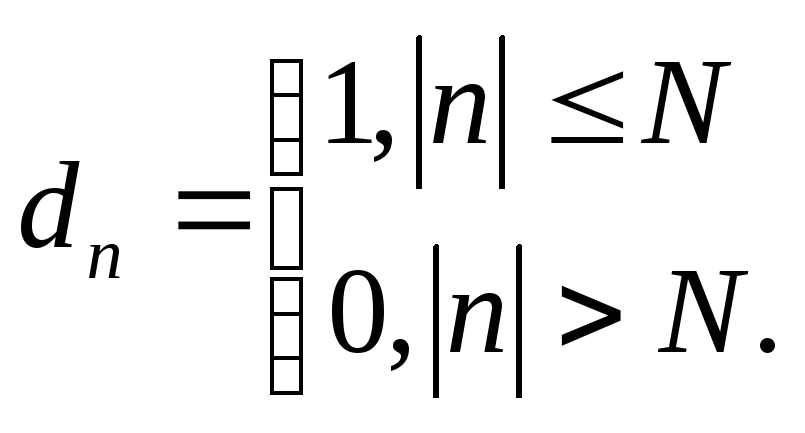
Функцию, имеющую коэффициенты Фурье d_nможно получить, просуммировав соответствующий ряд Фурье.

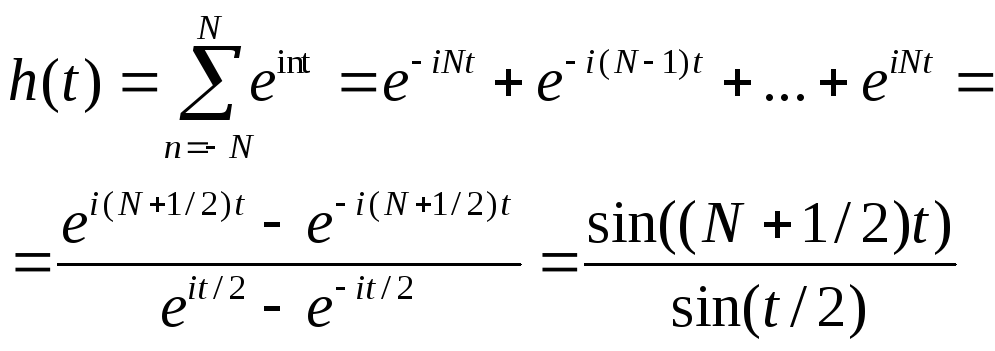
Таким образом, с помощью коэффициентов d_nусеченный ряд Фурье для функции f(t) можно представить в виде бесконечного ряда, но для функции, коэффициенты Фурье которой есть с_nd_n. такой функцией является свертка функций f(t) и h(t),т.е.

Таким образом, усеченный ряд Фурье для f(t) эквивалентен ее свертыванию с

При этом функцию h(t) называют свертывающим окном. Т.к. при больших N h(t) быстроколеблющаяся функция с максимальным значением (2N+1) в нуле и резко спадающая в обе стороны от нуля, то при свертке с прямоугольным импульсом возникают осцилляции, составляющие явление Гиббса. Эта неравномерная сходимость (явление Гиббса) может быть уменьшена путем использования менее резкого усечения рядов Фурье с помощьюокон данных различной модификации. Например:

Окно Бартлета: (N,n)=1-n/N, 0<n<N

Окно Ханнинга: (N,n)=1/2[1-cos(2n/N)], 0<n<N

Окно Хамминга: (N,n)= 0.54- 0.46cos(2n/N), o<n<N

И т. д.

Приближенное выражение для искомой функции будет даваться частичной суммой ряда: