Электрические цепи с распределенными параметрами

Линейные Нелинейные

постоянного переменного тока постоянного переменного ток

тока тока

Стационарные режимы и переходные процессы

Система ЛУ Система ДУ

 такие электрические цепи которые нельзя описать ДУ в полных производных. Это цепи у которых необротимые изменения как во времени так и по координате (расстояние (длина), температура, давление и т.п.)

В этом разделе будем рассматривать длинные линии или цепи сводящиеся к длинным линиям.

§ 1 Вывод уравнений однородной линии

i₁ i₂ Эту цепь можносчитать

R m П Н П

L C_кМ L Zн U₂

U₁

x xdx

Возмем элемент длиною линии dx или еденицу длиною линии

Всегда можно принять что на самом меньшем отрезке dx сопротивление

постоянны |a|

Введем эти параметры в dx

L₀ R₀ L₀ R₀ L₀ R₀

i

u g₀ c₀ g₀ c₀

dx dx

Если на  расстояний x элемент dx образует одинаковые L₀;R₀ её называют однородной.

Тогда в этих условиях используется законы К – а можно составить уравнение линии

Тогда в этих условиях используя за –ны К-а можно составить уравнение линии

Пусть к началу элемета длина линии входящий ток был равен i. Тогда по 1- му закону К-а выходящий ток будет равен

По 2 –му закону К- а для выбранного контура уравнение примет вид

По 1- му закону К-а для узла (a)

Принебригая величинами второго порядка малости последнее

Уравнение примет вид

1)

§ 2 Рушение уравнений однородной линии для утсановившегося синосоидального режима

Пусть на входе линии

Тогода все токи и направления на расстоянии x от начала линии будет изменятся во времени так же по синусоидальному закону (т. к. r_0­­, g₀,L₀)

L₀ - постоянная величина линия однородная

Последнее утверждение позволяет избавится от частных производных в уравниниях 1) если записать их в комплексных величинах.

- напряжение на расстоянии x от начала линии

- ток на расстоянии x от начала линии

Правая часть может быть записана

(2)

Решим систему (2) относительно напряжения для этого верхнее уравнение продифиренцируем по x

тогда с учетом нижнего уравнения, уравнение примет вид

(3)

- коэффициент расспределения

Решение (3) – частный случай обыкновенного ДУ

Хар. Ур.

Тогда решение для может быть записано

и нахидим из н.х.

Найдем решение для тока

- волновое сопротивление однородной линии

При x=0 определим A₁и A₂

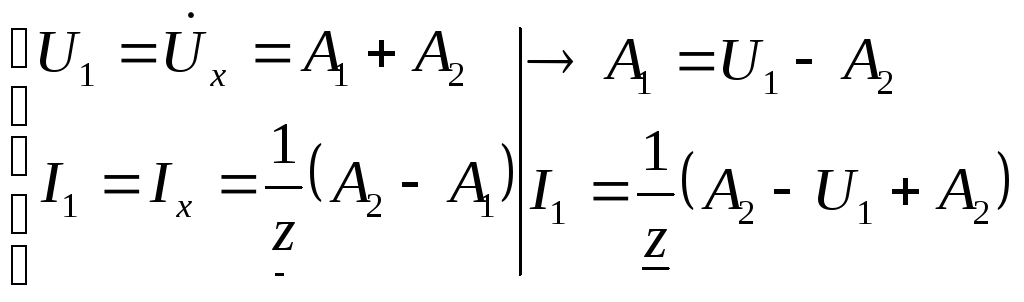
(4)

§ 3 Прямая и обратная волна напряжения и тока однородной линии

В решениях (4) слагаемые с множителем образуют прямую волну. Соответственно для

напряжения - прямая волна напряжиния

- прямая волна тока.

Опр Волна – прямая если с увеличением x её амплитуда уменьшается

Составляющая решение (4) содержащие множитель обрузуют отражающую или обратная волна

Опр Волна – обратимая если с увеличением х ее амплитуда увеличивается

Вывод Одновременно в линии  два вида волн: прямая и отраженная и является важной задача сформулировать такой режим работы чтобы обеспечить отсутствие отраженной волны

Рассмотрим временные функции этих волн. Для этого

ix(t)=

Отсюда становится очевидно что с  х амплитуда тока и напряжения уменьшается по экспоненциальному закону. Например напряжение

Ux

Ux(x) x

-U₁

- момент времени

Пусть t₁>t₂

При прямая волна напряжения и тока с течением времени движется от конца линии к ее началу

С какой скоростью будет бежать эта волна ? Определим скорость движения прямой волны от ее конца к началу

При ф-я имеет вид

длина волны

- скорость бега прямой волны.

Рассмотрим обратное волне напряжения и тока

Uxобр

U_1обр t₁

x

 2 3 -U₁обр

t₂>t₁

Изобразим взаимное соответствие прямой и обратной волн

U_пр

x

0

§ 4 Связь уравнений линии с уравнениями четырехполюсника

U₂ - напряжние в конце линии при х=l U_2l

I₂ - ток в конце линии при х=l I_2l

Тогда напряжение на расстоянии

Введем

х_{2 –} расстояние от конца лнии

для теории линии для установившегося sin режима

x₁- расстояние от начала линии

§ 5 Неискажающая линия

Линию у которой