Новая папка / Глава 8.2Нелинейные эл.цепи пост.тока

РАЗДЕЛ

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ.

Цепь нелинейная если хотя бы один из её элементов обладает нелинейной характеристикой.

Характеристика элемента, проходящая в первом и в третьем квадрантах, когда положительному значению тока соответствующее точке 1 равное значению тока в точке 2при таких же значениях напряжения - симметричная .

R(u) , R(i) – ВАХ(вольт - амперная характеристика)

Так обозначается полупроводниковый диод. Он относится к неуправляемым элементам.

Его ВАХ.

НЕЛИНЕЙНЫЕ L – ЭЛЕМЕНТЫ.

Y =LI – вебер – амперная характеристика(ВбАХ)

L = Const – линейные , но если L сделана из ферромагнетика то это неуправляемая и симметричная индуктивность.

w = const

Iy = const то есть дополнительно создаётся Y.

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА.

Дано. U r(U)

Определить. I - ?

1. Если r(U) задано графиком (ВАХ) то тогда решение простое:

Такой метод расчета называют графическим, но точность расчета очень невысока. Этот метод ещё называют предварительным.

2) Если r(U) выразить аналитически, подобрав закон изменения r(U) как функцию f = r(U).

Тогда

I = U/r но r зависит от I (r(I)) следовательно I = U/r(I) и находится методом подбора.

РАСЧЁТ НЕЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ.

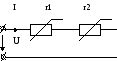
Дано. U , BAX1, BAX2.

Определить: I - ?

Так как I в нагрузках один и тот же, то методом выбранных значений строим суммарную ВАХ.

РАСЧЁТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ.

РАСЧЁТ НЕЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА ПРИ СМЕШАНОМ СОЕДИНЕНИИ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ.

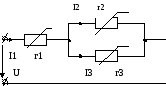
Дано: U, BAX1,2,3

Определить: I1,I2,I3.

СТАТИЧЕСКОЕ И ДИФФЕРЕНЦИАЛЬНОЕ СОПРОТИВЛЕНИЕ В НЕЛИНЕЙНЫХ ЦЕПЯХ.

U1/I1 = R = U2/I2 r1ст = U1/I1 r2ст = U2/I2

tgf=rст

Отношение напряжения к току фиксированной точки характеристики называют статическим сопротивлением.

Если же необходимо рассматривать быстроизменяющиеся процессы в нелинейной цепи пользуются понятием дифференциального сопротивления.

Дифференциальное сопротивление, – когда в области выбранной точки характеристики определяется касательная к характеристике и тогда tga a – угол наклона этой касательной к оси токов называют дифф.сопротивлением. tga = rдиф = dU/dI

РАСЧЁТ НЕЛИНЕЙНЫХ МАГНИТНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА.

Материал характеризуется B(H) и характеристика нелинейная.

По закону полного тока можно определить напряженность магнитного поля.

Тогда HL = IW H = IW/L. Тогда появится В и тогда

Y = WФ Таким образом, эту магнитную цепь можно представить эквивалентной электрической цепью.

Найдём rm

Если даны I, W, геометрические размеры, В(Н) и нужно найти Ф – ? то необходимо выполнить:

Если rm(Ф) задана тогда:

Фпр Фр

Ф1пр Ф1р

Ф2пр Ф2р

Если Фnпр = Фnр то задача решена.

РАСЧЁТ НЕЛИНЕЙНОЙ МАГНИТНОЙ ЦЕПИ МЕТОДОМ ДВУХ УЗЛОВ.

L1 Ф1 a Ф3 L3

I1 I3

Ф2

L2

S2

S1 b S3

Переведём В(Н) в Ф1(Um1), Ф2(Um2),Ф3(Um3)

Ф = В S

Um = HL = IW – второй закон Кирхгофа для магнитной цепи.

Ф1 = В S1 Um1 = H L1

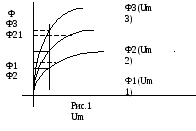
Приведём характеристики Ф(Um) к одному магнитному напряжению.

Um – Umab = -F1

Umab = Um1 + F1

Umab = Um3 – F3

Umab = Um2

Сумма всех Ф равна 0.

Ф1 + Ф2 + Ф3 = 0 = f(Umab)

Решим эту же задачу методом двух узлов с использованием метода итераций.

1)

2)

3)

4)

См. рис.1

U0	rm1	rm2	rm3	Umab
0	rm10	rm20	rm30	Umab0
	rm11	rm21	rm31	Umab1

Подставляем найденные m1 сопротивления 0-й итерации в формулу (1) и получаем Um10 и его подставляем в формулы 2), 3), 4) и получаем

Ф1	Ф2	Ф3
Ф11	Ф21	Ф31
Ф12	Ф22	Ф32

И до тех пор, пока сумма всех Ф не будет равна нулю. То есть Ф1 + Ф2 + Ф3 = 0.