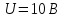- •2013 Задание
- •1 Расчет и выбор элементов электропривода. Построение графиков переходных процессов при подаче на вход системы ступенчатого сигнала
- •2 Проектирование система автоматического регулирования скорости
- •3 Графики переходных процессов двухконтурной системы регулирования скорости
- •5 Проектирование системы автоматического регулирования положения
- •6 Графики переходных процессов трехконтурной системы регулирования положения
- •8 Лачх и лфчх для всех замкнутых контуров регулирования
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Комсомольский-на-Амуре государственный
технический университет»
Электротехнический факультет
Кафедра электропривода и автоматизации промышленных установок
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине «Моделирование систем»
Моделирование системы управления следящего
электропривода
Студент группы 9АУб-1 И.Е. Бичаев
 Преподаватель
А.С. Гудим
Преподаватель
А.С. Гудим
2013 Задание
1 Спроектировать двухконтурную систему автоматического регулирования скорости. Настройку контуров регулирования произвести на модульный оптимум. В качестве объекта управления использовать двигатель постоянного тока независимого возбуждения. Параметры двигателя выбрать согласно заданному варианту.
2
Получить графики переходных процессов
замкнутой системы автоматического
регулирования по управляющему воздействию
для скорости и сигнала управления в
случае ступенчатого и синусоидального
воздействия. На графиках переходных
процессов необходимо отобразить
поведение системы без нагрузки, с
набросом нагрузки, со съемом нагрузки.
В качестве нагрузки использовать
постоянную нагрузку
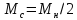 .
.
3 Дополнить полученную систему автоматического регулирования скорости контуром положения. Настройку контура положения произвести на симметричный оптимум.
4 Получить графики переходных процессов замкнутой скорректированной системы автоматического регулирования по управляющему воздействию для положения, для ошибки по току, для скорости.
5 Определить перерегулирование в системе автоматического регулирования скорости (положения), время переходных процессов, в случае работы системы в случае подачи на вход системы U = 10B.
6 Для всех замкнутых контуров регулирования представить ЛАЧХ и ЛФЧХ.
7 Представить в приложении листинг созданного «m-файла», все промежуточные расчеты должны быть выполнены в Matlab.
1 Расчет и выбор элементов электропривода. Построение графиков переходных процессов при подаче на вход системы ступенчатого сигнала
В качестве объекта управления (ОУ) используется двигатель постоянного тока независимого возбуждения (ДПТ НВ).
Исходные данные (ДПТ НВ модели П91):
Рн = 43000 Вт – номинальная мощность;
nн = 1450 об/мин – номинальное количество оборотов в минуту;
Uн = 2700 В – номинальное напряжение;
Iн = 159 A – номинальный ток;
η = 86,5 – КПД;
Jн = 5,9 кг∙м2 – номинальный момент двигателя.
Для силовой части электропривода выберем трехфазную мостовую схему реверсивного преобразователя с совместным управлением. Преобразовательный трансформатор не используется.

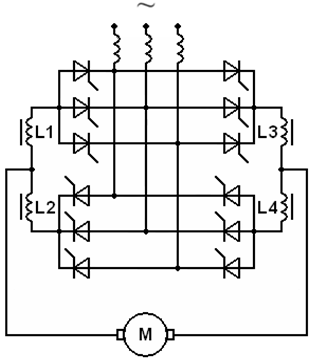
Рисунок 1 – Силовая часть реверсивного преобразователя
Схема регулирования скорости – двухконтурная. Внутренний контур – контур регулирования тока, внешний – контур регулирования скорости.
Определим
значение ЭДС холостого хода преобразователя
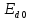 ,B:
,B:
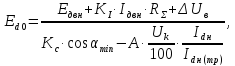
где
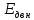 – номинальное значение ЭДС двигателя,
В:
– номинальное значение ЭДС двигателя,
В:
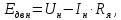
где
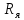 – сопротивление якорной цепи двигателя,
Ом:
– сопротивление якорной цепи двигателя,
Ом:
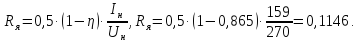
Таким образом:
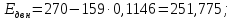
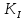 –коэффициент
загрузки по току,
–коэффициент
загрузки по току,
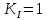 ;
;
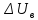 –напряжение
спрямления ВАХ тиристора,
–напряжение
спрямления ВАХ тиристора,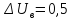 В;
В;
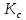 –коэффициент,
определяющий возможные колебания
напряжения в питающей сети,
–коэффициент,
определяющий возможные колебания
напряжения в питающей сети,
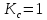 ;
;

 –минимальный
угол управления тиристорным
преобразователем,
–минимальный
угол управления тиристорным
преобразователем,
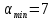 эл. градусов;
эл. градусов;
А – коэффициент наклона внешней характеристики трехфазной мостовой схемы, А = 0,5;
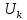 –напряжение
короткого замыкания,
–напряжение
короткого замыкания,
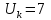 ;
;
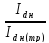 –коэффициент,
определяющий степень загрузки
преобразовательного трансформатора,
–коэффициент,
определяющий степень загрузки
преобразовательного трансформатора,
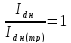 ;
;
Далее
определим суммарное активное сопротивление
цепи выпрямленного тока
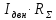 ,
В:
,
В:
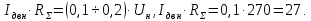
Учитывая
значения, найденные выше, определим
значение ЭДС холостого хода преобразователя
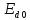 ,B:
,B:
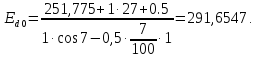
Выбор сглаживающего дросселя:
В трехфазной мостовой схеме амплитудные значения гармонических составляющих выпрямленного напряжения Udm связаны с его значением Udo следующим выражением:
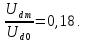
Следовательно,
амплитудное значение гармонических
составляющих выпрямленного напряжения
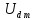 ,
В:
,
В:
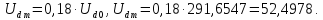
Индуктивность,
требуемая для обеспечения допустимого
значения пульсаций выпрямленного тока
в цепи нагрузки
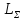 ,
Гн:
,
Гн:
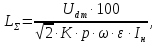
где ω – круговая частота сети, ω = 314 с-1;
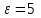 ;
;
 K∙p
– произведение кратности гармоники на
число пульсаций, K∙p
= 6;
K∙p
– произведение кратности гармоники на
число пульсаций, K∙p
= 6;
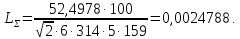
Требуемое значение индуктивности сглаживающего дросселя определяется по соотношению:
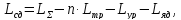
где n – число фазных обмоток трансформатора, находящихся в цепи выпрямленного тока (n = 0, так как трансформатор не используется);
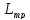 –индуктивность
фазы преобразовательного трансформатора,
приведенная к вторичной обмотке,
–индуктивность
фазы преобразовательного трансформатора,
приведенная к вторичной обмотке,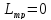 Гн;
Гн;
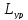 –индуктивность
уравнительного
реактора, Гн;
–индуктивность
уравнительного
реактора, Гн;
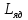 –индуктивность
якоря двигателя, Гн;
–индуктивность
якоря двигателя, Гн;
Индуктивность якоря двигателя определим по формуле:
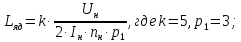
Используя эти данные, получим:
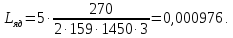
При
управлении реверсивным преобразователем
применяют уравнительный реактор,
индуктивность которого
 (Гн) равна:
(Гн) равна:
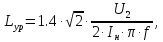
где
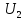 – коэффициент запаса по напряжению, В:
– коэффициент запаса по напряжению, В:
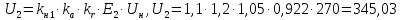
Таким образом:
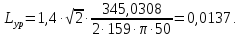
 Требуемое
значение индуктивности сглаживающего
дросселя:
Требуемое
значение индуктивности сглаживающего
дросселя:
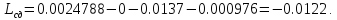
Так
как значение
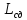 отрицательное, следовательно, сглаживающий
дроссель не нужен.
отрицательное, следовательно, сглаживающий
дроссель не нужен.
Расчёт постоянных времени:
Электромагнитная
постоянная времени
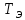 ,
с:
,
с:
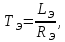
где
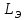 – эквивалентная индуктивность цепи
преобразователь-двигаель, Гн;
– эквивалентная индуктивность цепи
преобразователь-двигаель, Гн;
 –эквивалентное
активное сопротивление цепи, Ом.
–эквивалентное
активное сопротивление цепи, Ом.
Эквивалентная индуктивность цепи определяется по формуле:
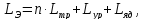
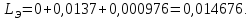
Эквивалентное активное сопротивление цепи определяется по формуле:
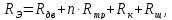
где
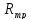 – приведенное активное сопротивление
фазы трансформатора,
– приведенное активное сопротивление
фазы трансформатора,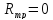 Ом;
Ом;
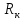 –коммутационное
сопротивление двигателя,
–коммутационное
сопротивление двигателя,
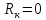 (т.к.
(т.к.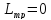 )
Ом;
)
Ом;
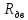 –активное
сопротивление двигателя,
–активное
сопротивление двигателя,
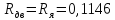 (Ом);
(Ом);
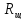 –активное
сопротивление щеточного контакта, Ом:
–активное
сопротивление щеточного контакта, Ом:
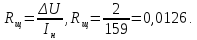
Рассчитаем эквивалентное активное сопротивление цепи:
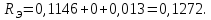
Тогда электромагнитная постоянная времени равна:
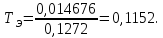
 Суммарный
момент инерции
Суммарный
момент инерции
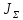 ,
м∙кг2:
,
м∙кг2:
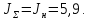
Номинальная
скорость вращения якоря
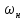 ,
с-1:
,
с-1:
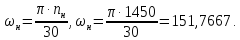
Номинальный
момент
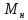 ,
Н∙м:
,
Н∙м:
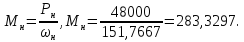
Коэффициент пропорциональности равен:
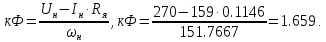
Передаточный коэффициент цепи обратной связи по скорости:
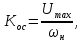
где
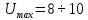 В, выбираем
В, выбираем
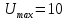 В.
В.
Таким образом:
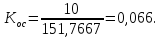
Передаточный коэффициент цепи обратной связи по току:
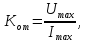
где
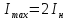 А, выбираем
А, выбираем
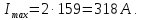
Таким образом:
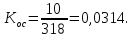
Электромеханическая
постоянная времени
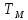 ,
с:
,
с:
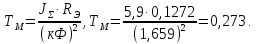
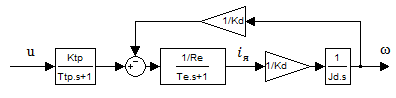
 Рисунок
2 – Модель двигателя постоянного тока
независимого возбуждения с учетом
влияния ЭДС двигателя
Рисунок
2 – Модель двигателя постоянного тока
независимого возбуждения с учетом
влияния ЭДС двигателя
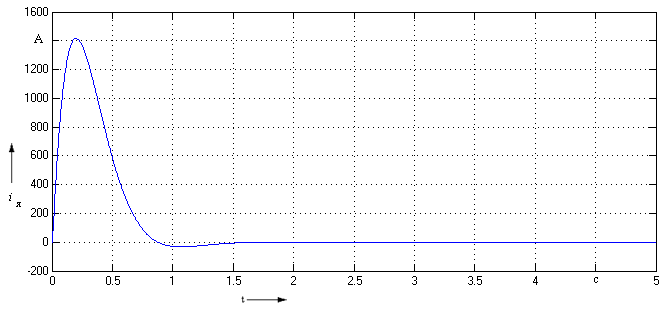
Рисунок
3 – Реакция тока якоря на задающее
воздействие
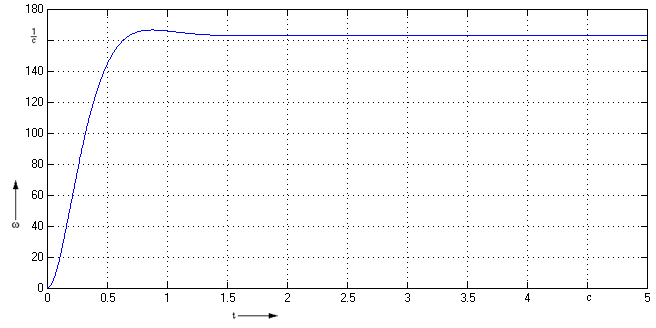
Рисунок
4 – Реакция системы на задающее воздействие