ПЗ 10-17 Линейная алгебра( Э)

5

ПЗ-6. (Лекция 10-11) Пространство арифметических векторов. Базис и ранг системы векторов.

Задача 1. Даны вектора . Найти координаты векторов

Задача 2. Вычислить координаты линейной комбинации заданных векторов:

а) 5а₁+4а₂-2а₃, если а₁ = (5; -3; 1; 6), а₂ = (4; -1; 1; 2) и а₃ = (0;1;-1;1);

б) -а₁+3(а₂-1/2а₃), если а₁ = (-3; 1; 6), а₂ = (8; 1; 2) и а₃ = (9;3;-1);

Задача 3. Выяснить, являются ли векторы а₁ = (5; -3; 1; 6),

а₂ = (4; -1; 1; 2) и а₃ = (0;1;-1;1) линейно зависимыми.

Задача 4. Исследовать на линейную зависимость систему векторов:

1)

2. 

Задача 5. Выяснить, являются ли базисом соответствующего пространства Rⁿ следующие системы векторов:

1. (1; 1), (-1; 1);

2. (1; 1; 1), (1; 0; 1), (2; 1; 2);

Задача 6. Выяснить, разлагается ли вектор В по системе векторов А₁, А₂,если В=(2;3), A₁=(1;2), A₂=(2;1).

Задача 7. Даны векторы a = e₁ + e₂ + e₃, b = 2e₂ + e₃, c = e₂ + 5e₃ – базис линейного пространства. Доказать, что векторы a,b,c образуют базис. Найти координаты вектора d = 2e₁ – e₂ + e₃ в базисе a,b,c.

ДЗ-6. Пространство арифметических векторов. Базис и ранг системы векторов.

Задача 1. Даны вектора . Найти координаты векторов

Задача 2. Исследовать на линейную зависимость следующую систему векторов:

Задача 3. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. А₁=(-4;2;8), A₂=(14;-7;-28);

2. А₁=(0;1;1;0), A₂=(1;1;3;1), A₃=(1;3;5;1), A₄=(0;1;1;-2);

Задача 4. Найти размерность и базис системы векторов. Записать разложение векторов системы по найденному базису.

а)

в)

ПЗ 7. (Лекция 12-13) Пространства со скалярным произведением. Линейные операторы.

Задача 1. Даны векторы . Вычислить длины этих векторов, угол между ними и скалярное произведение указанных векторов:

Задача 2. Применяя процесс ортогонализации, построить ортогональную систему векторов: a₁=(0;1;1), a₂=(1;1;1), a₃=(-3;3;1).

Задача 3. Пусть Являются ли линейными следующие преобразования?

Задача 4. Пусть в пространстве R³ линейный оператор А,

в базисе е₁, е₂, е ₃ задан матрицей 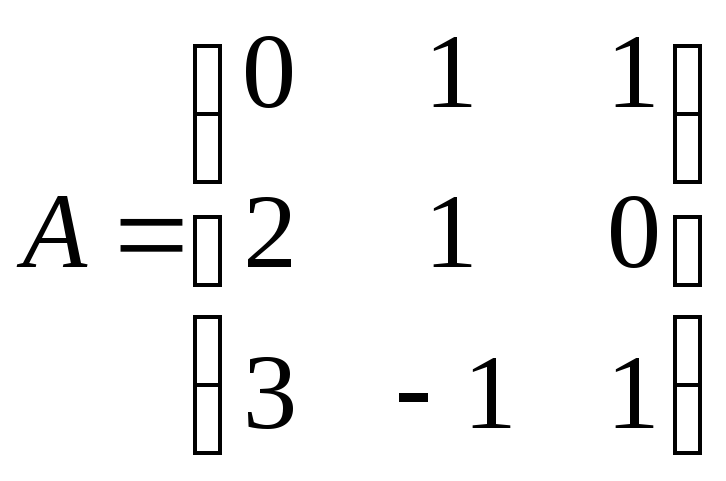. Найти образ у = А(х) вектора х = 5е₁ + 8е₂ -2е₃.

Задача 5. Найти указанное преобразование.

Пусть Найти

Задача 6. Найти координаты вектора в базисе если он задан в базисе .

.

Задача 7. Найти матрицу линейного преобразования в базисе если она задана в базисе

, .

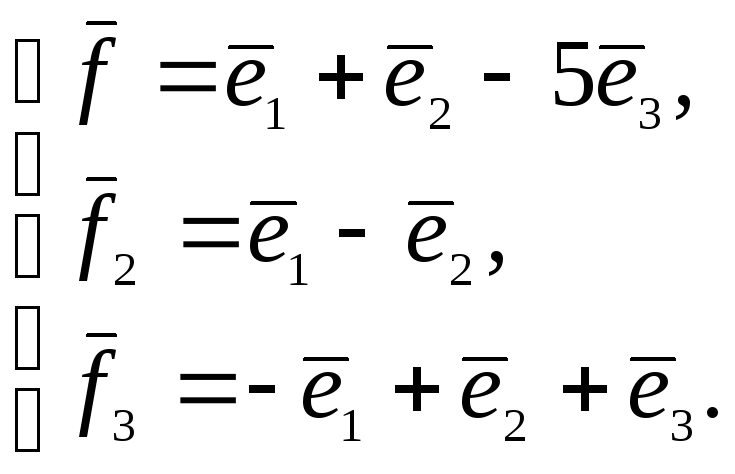ДЗ-7. Пространства со скалярным произведением. Линейные операторы.

Задание 1. Векторы e₁, e₂, e₃, e₄, e₅ образуют ортонормированный базис. Найти скалярное произведение и длины векторов x = e₁ - 2e₂ + e₅, y = 3e₂ + e₃ – e₄ + 2e₅.

Задача 2. Вычислить косинус угла, образованного векторами

.

Задача 3. Применяя процесс ортогонализации, построить ортогональную систему векторов: a₁=(1;-1;1), a₂=(2;1;N), a₃=(3;N;1).

Задача 4. Пусть Являются ли линейными следующие преобразования?

Задача 5. Найти указанное преобразование.

Пусть Найти

Задача 6. Линейный оператор А в базисе е₁, е₂ задан матрицей Найти образ у = А(х), где х = (N+1)е₁ – 3е₂ .

ПЗ-8. (Лекция 14-15) Собственные значения и собственные векторы линейного оператора. Привидение квадратной матрицы к диагональному виду.

Задача 1. Найти собственные числа операторов А и С, если его матрицы имеют вид:

.

Задача 2.Найти собственные числа и собственные вектора оператора, если его матрица имеет вид: .

Задача 3. Привести матрицы линейных операторов В и Р к диагональному виду, если:

.

Задача 4. Привести матрицу линейного оператора В к диагональному виду, если

ДЗ-8. Собственные вектора и собственные числа линейных операторов.

Задание 1.Найти собственные числа операторов, если его матрицы имеют вид: .

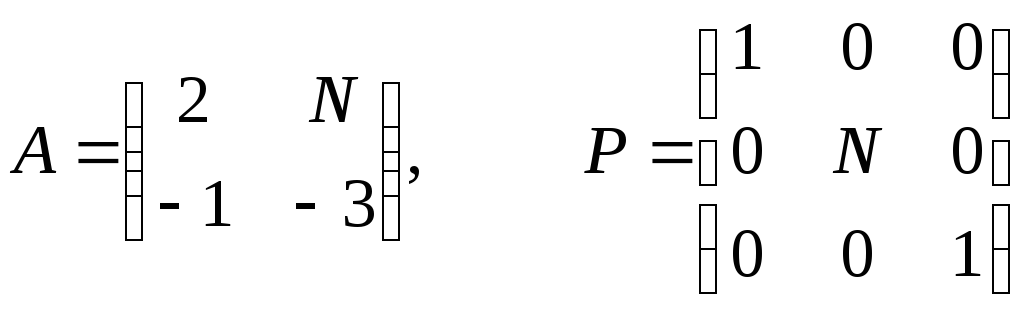Задача 3. Привести матрицы линейных операторов В и Р к диагональному виду, если:

Задание 2. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей

.

ПЗ – 9. (Лекция 16) Квадратичные формы.

Задание 1. Записать квадратичные формы в матричном виде:

1. L(x₁, х₂, х₃) = 2х₁² + 4х₁х₂ - 2х₁х₃ - 5х₂² + 8x₃² + 6x₂x₃.

2. L(x₁, х₂, х₃) = - х₁² + 2х₁х₂ + 2х₂х₃ + 2х₂² - 3x₃².

3. L(x₁, х₂, х₃) = 2х₁х₂ + 4х₁х₃ – 6x₂x₃.

Задание 2. Привести к каноническому виду квадратичную форму 9x²+24xy+16y².

Задание 3. Дана квадратичная форма L(x₁,x₂) = 3x₁² – x₂² +4x₁x₂. Найти квадратичную форму, полученную из данной линейным преобразованием x₁ = 2y₁ – y₂, x₂ = y₁ + y₂.

ДЗ-9.

Задание 1. Записать квадратичные формы в матричном виде:

1. L(x₁, х₂, х₃) = Nх₁² + 4Nх₁х₂ - 4х₁х₃ - 5х₂² + Nx₃² + 8x₂x₃.

2. L(x₁, х₂, х₃) = - х₁² + 12х₁х₂ + 2х₂х₃ + Nх₂² - 7x₃².

3. L(x₁, х₂, х₃) = 6х₁х₂ + 2Nх₁х₃ – 4x₂x₃.