
РГЗ-Mathсad
.docРасчетно-графическое задание
Задание 1. Решить
систему линейных уравнений методом
Гаусса, сделать проверку. Доказать
совместность, т.е.
![]() .
.
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)
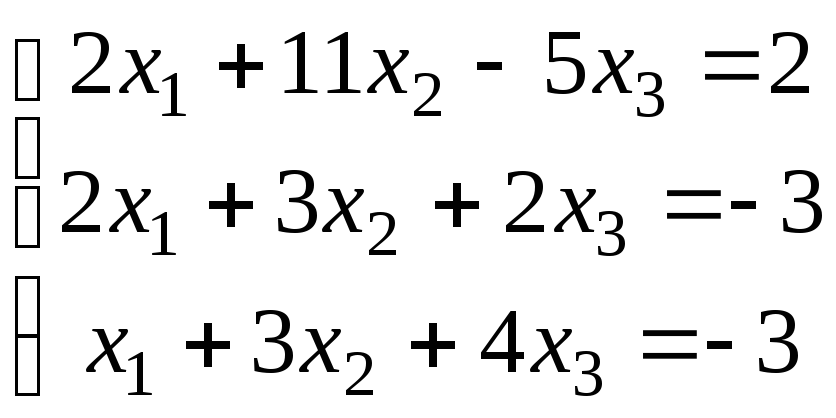
11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
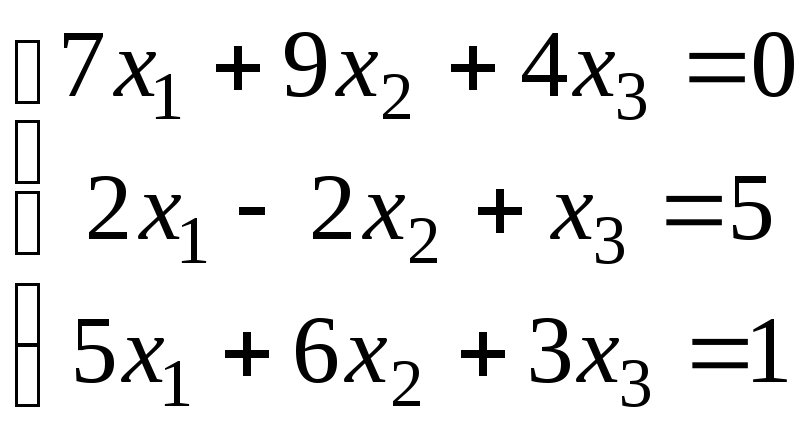 20)
20)
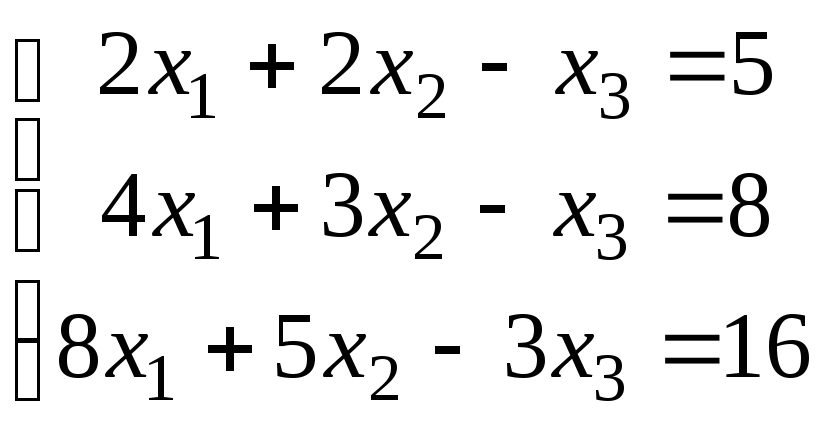
21)

2. Построить график
функции
![]() .
Найти точки разрыва, точки экстремума,
точки перегиба. Определить уравнения
асимптот.
.
Найти точки разрыва, точки экстремума,
точки перегиба. Определить уравнения
асимптот.
1)
 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]()
Задание 3. Найти
решение дифференциального уравнения
второго порядка
![]() методом Рунге-Кутты с заданными начальными
условиями.
методом Рунге-Кутты с заданными начальными
условиями.
1)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]()
2)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
3)
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
4)
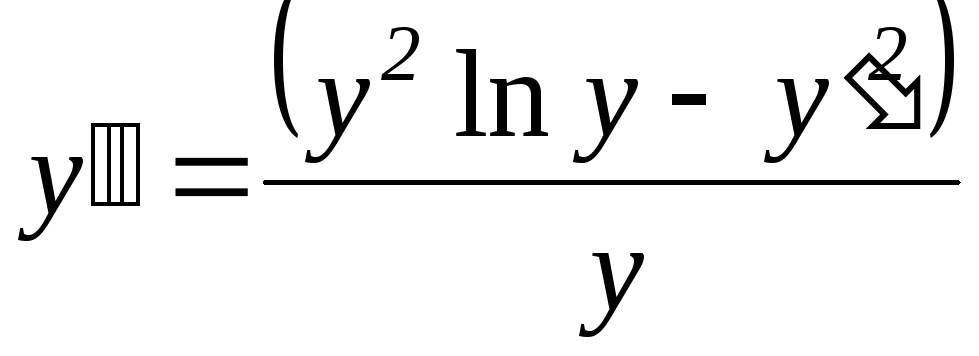 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
5)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
6)
 ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
7)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
8)
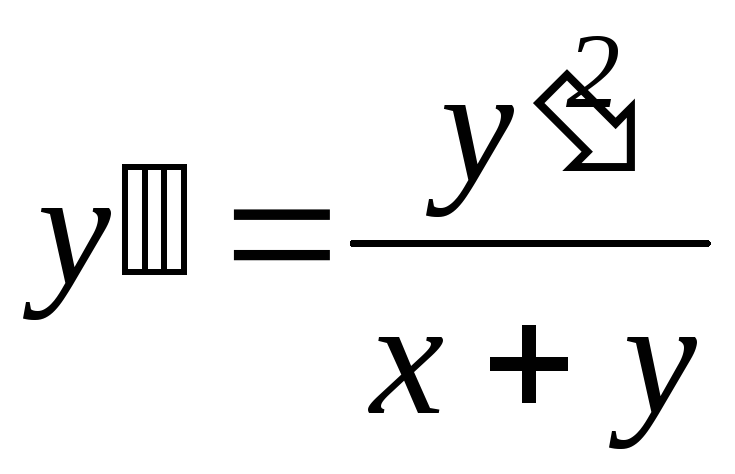 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
9)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
11)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
12)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
13)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
14)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
15)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
16)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
17)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
18)
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
19)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
20)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
21)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задание 4. Постройте
биномиальное распределение для серии
![]() независимых испытаний с вероятностью
успеха
независимых испытаний с вероятностью
успеха
![]() ,
пуассоновское распределение с параметром
,
пуассоновское распределение с параметром
![]() ,
геометрическое распределение с
параметрами
,
геометрическое распределение с
параметрами
![]() ,
,
![]() .
Для каждого распределения выполните
следующие:
.
Для каждого распределения выполните
следующие:
-
проверить равенство
 ,
где
,
где
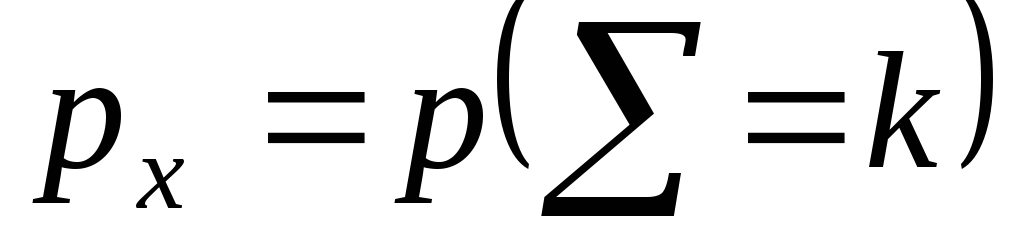
-
построить графики распределения и функций распределения
-
вычислить вероятность попадания значений случайной величины в интервал

1)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
7)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
8)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
9)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
11)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
12)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
13)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
14)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
15)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
16)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
17)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
18)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
19)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
20)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
Теоретическая часть
Для решения системы уравнений методом Гаусса необходимо:
-
Задать ORIGIN:=1.
-
Сформировать расширенную матрицу системы, используя функцию augment(C,d), которая формирует матрицу, добавляя к столбцам матрицы С справа столбец правых частей d:
Cr:= augment(C,d)
-
Задать Cg:=rref(Cr). Последний столбец матрицы Cg содержит решение системы.
-
Функция submatrix, выделяя последний столбец матрицы Cg, формирует решение системы.
Для того чтобы исследовать функцию и построить ее график необходимо:
-
Определите функцию и постройте ее график.
-
Найти точку пересечения с осью ординат, вычислив f(0). Найти точку пересечения с осью абсцисс, решив уравнение f(x)=0 (через меню Символика).
-
Найти точки разрыва функции. Вычислить односторонние пределы.
-
Записать уравнения вертикальных асимптот:
 – вертикальная асимптота, если существуют
пределы:
– вертикальная асимптота, если существуют
пределы:
 ,
, .
. -
Записать уравнение наклонной асимптоты:
 – наклонная асимптота, если существуют
пределы:
– наклонная асимптота, если существуют
пределы:
 ,
,
 .
. -
Записать уравнения горизонтальных асимптот y=a. Изобразить асимптоты на графике.
-
Исследовать функцию на четность и периодичность.
-
Найти нули производной, решив уравнение
 .
Вычислить и записать координаты точек
экстремума, указать их тип (максимум,
минимум). Построить график производной.
.
Вычислить и записать координаты точек
экстремума, указать их тип (максимум,
минимум). Построить график производной. -
Найти нули второй производной, решив уравнение
 .
Вычислить и записать координаты точек
перегиба. Описать интервалы выпуклости
и вогнутости. Построить график второй
производной.
.
Вычислить и записать координаты точек
перегиба. Описать интервалы выпуклости
и вогнутости. Построить график второй
производной.
Для того чтобы решить дифференциальное уравнение второго порядка методом Рунге-Кутты необходимо:
-
Свести ее к задаче для эквивалентной нормальной системы второго порядка, обозначив
 и
и
 .
Тогда
.
Тогда
 .
. -
Затем задачу решить численно с использованием алгоритма Рунге-Кутты с указанием числа узлов N=30.
Биномиальное распределение (схема Бернулли):
Пусть
![]() - случайная величина, равная числу
успехов в серии из n
испытаний. Эта величина принимает целые
значения от 0
до n,
p
– вероятность успеха, q
= 1-p
– вероятность неудачи в каждом испытании.
- случайная величина, равная числу
успехов в серии из n
испытаний. Эта величина принимает целые
значения от 0
до n,
p
– вероятность успеха, q
= 1-p
– вероятность неудачи в каждом испытании.
Распределение
![]() называется биномиальным
и определяется формулой Бернулли
называется биномиальным
и определяется формулой Бернулли
![]() ,
,
где 0<p<1,
k=0,1,…,n,
![]() .
.
Mathcad
строит точки
![]() и, соединяя линией, получает так называемую
плотность распределения (на графике –
непрерывная линия). Ей соответствует
функция распределения.
и, соединяя линией, получает так называемую
плотность распределения (на графике –
непрерывная линия). Ей соответствует
функция распределения.
Для вычисления
плотности вероятности и функции
распределения случайной величины,
имеющей биномиальное распределение,
предназначены функции dbinom(k,n,p)
и pbinom(k,n,p),значения
которых соответственно
![]() и F(k).
и F(k).
Геометрическое распределение:
Пусть
![]() - число испытаний до первого успеха,
- число испытаний до первого успеха,
![]() меняется от 0
до
меняется от 0
до
![]() ,
и ее распределение определяется формулой
,
и ее распределение определяется формулой
![]() ,
k=0,1,…,
0<p<1,
q=1-p.
,
k=0,1,…,
0<p<1,
q=1-p.
Используя формулу
бесконечно убывающей геометрической
прогрессии, можно показать, что
![]() .
Для вычисления плотности вероятности
и функции распределения случайной
величины, имеющей геометрическое
распределение, предназначены функции
dgeom(k,p)
и pgeom(k,p),
значения которых соответственно
.
Для вычисления плотности вероятности
и функции распределения случайной
величины, имеющей геометрическое
распределение, предназначены функции
dgeom(k,p)
и pgeom(k,p),
значения которых соответственно
![]() и F(k).
и F(k).
Пуассоновское распределение:
Данное распределение
имеет случайная величина
![]() ,
принимающая значения k=0,1,2,…
с вероятностями
,
принимающая значения k=0,1,2,…
с вероятностями
![]() ,
где
,
где
![]() - параметр распределения. При любых
- параметр распределения. При любых
![]() имеем
имеем
![]() .
.
Для вычисления
плотности вероятности и функции
распределения случайной величины,
имеющей пуассоновское распределение,
предназначены функции dpois(k,![]() )
и ppois(k,
)
и ppois(k,![]() ),
значения которых соответственно равны
),
значения которых соответственно равны
![]() и F(k).
и F(k).
Так как случайная величина на графике представлена как непрерывная, то вероятность того, что ее значение попадет в интервал (a,b), вычисляется здесь как для непрерывной по формуле:
P(a<![]() <b)=F(b)-F(a).
<b)=F(b)-F(a).
