59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии

Основным условием проведения теста Голдфелда-Квандта является предположение о нормальном законе распределения случайной ошибки βi модели регрессии.

Рассмотрим применение данного теста на примере линейной модели множественной регрессии.

Предположим, что на основе проведённого исследования зависимость между переменными можно аппроксимировать линейной моделью множественной регрессии.

В модели множественной регрессии выбирается независимая переменная xik, от которой наиболее вероятно могут зависеть остатки модели ei.

На следующем этапе значения независимой переменной xik ранжируются

располагаются по возрастанию и делятся на равные 3 части.

Для I и III частей строятся две независимые модели регрессии вида:

Для каждой из построенных моделей регрессий рассчитываются суммы квадратов остатков:

Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:

Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы: k1=nI–l и k2=nI–l,  где l – число оцениваемых по данной выборке параметров.

Наблюдаемое значение F-критерия находят по формуле:

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза отвергается, и, следовательно, в модели регрессии присутствует гетероскедастичность, зависящая от переменной xik.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл‹Fкрит, то основная гипотеза принимается, и гетероскедастичность в модели множественной регрессии не зависит от переменной xik.

На следующем этапе проверяются другие независимые переменные, если есть предположение об их тесной связи с G2(εi).

Если тест Голдфелда-Квандта проводился для линейной модели парной регрессии, то вывод о принятии основной гипотезы означает гомоскедастичность построенной модели регрессии.

60. Устранение гетероскедастичности остатков модели регрессии

Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.

Наиболее простым методом устранения гетероскедастичности остатков модели регрессии является взвешивание параметров модели регрессии. В этом случае отдельным наблюдениям независимой переменой, характеризующимся максимальным среднеквадратическим отклонением случайной ошибки, придаётся больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придаётся меньший вес. После данной процедуры свойство эффективности оценок неизвестных коэффициентов модели регрессии сохраняется.

Если для устранения гетероскедастичности был использован метод взвешивания, то в результате мы получим взвешенную модель регрессии с весами

Предположим, что на основе имеющихся данных была построена линейная модель парной регрессии, в которой было доказано наличие гетероскедастичности остатков

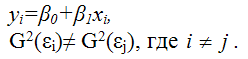
Рассмотрим подробнее процесс взвешивания для данной модели регрессии.

Разделим каждый член модели регрессии на среднеквадратическое отклонение случайной ошибки G(βi):

В общем виде процесс взвешивания для линейной модели парной регрессии выглядит следующим образом:

Для более наглядного представления полученной модели регрессии воспользуемся методом замен:

В результате получим преобразованный вид взвешенной модели регрессии:

Преобразованная взвешенная модель регрессии является двухфакторной моделью регрессии.

Дисперсию случайной ошибки взвешенной модели регрессии можно рассчитать по формуле:

Полученный результат доказывает постоянство дисперсий случайных ошибок преобразованной модели регрессии, т. е. о выполнении условия гомоскедастичности.

Главный недостаток метода взвешивания заключается в необходимости априорного знания среднеквадратических отклонений случайных ошибок модели регрессии. По той причине, что в большинстве случаев данная величина является неизвестной, приходится использовать другие методы, в частности методы коррекции гетероскедастичности.

Определение. Суть методов коррекции гетероскедастичности состоит в определении оценки ковариационной матрицы случайных ошибок модели регрессии:

Для определения оценок

используется метод Бреуше-Пайана, который реализуется в несколько этапов:

1) после получения оценок неизвестных коэффициентов модели регрессии рассчитывают остатки ei и показатель суммы квадратов остатков

2) рассчитывают оценку дисперсии остатков модели регрессии по формуле:

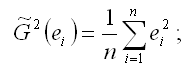
3) строят взвешенную модель регрессия, где весами являются оценка дисперсии остатков модели регрессии

4) если при проверке гипотез взвешенная модель регрессии является незначимой, то можно сделать вывод, что оценки матрицы ковариаций Ω являются неточными.

Если вычислены оценки дисперсий остатков модели регрессии, то в этом случае можно использовать доступный обобщённый или взвешенный методы наименьших квадратов для вычисления оценок коэффициентов модели регрессии, которые отличаются только оценкой

Если гетероскедастичность остатков не поддаётся корректировке, то можно рассчитать оценки неизвестных коэффициентов модели регрессии с помощью классического метода наименьших квадратов, но затем подвергнуть корректировке ковариационную матрицу оценок коэффициентов

т. к. условие гетероскедастичности приводит к увеличению данной матрицы.

Ковариационная матрица оценок коэффициентов

может быть скорректирована методом Уайта:

где N – количество наблюдений;

X– матрица независимых переменных;

– квадрат остатков модели регрессии;

– транспонированная i-тая строка матрицы данных Х.

Корректировка ковариационной матрицы оценок коэффициентов

методом Уайта приводит к изменению t-статистики и доверительных интервалов для коэффициентов регрессии.