ТЭЦ Лекция 11

3.2.2. Лекция 11

11.1. Три формы ряда Фурье

1. Всякая периодическая функция времени удовлетворяющая условиям Дирихле, (конечное число разрывов первого рода и конечное число экстремумов за период) имеет свой ряд Фурье.

2. Три формы ряда Фурье

б. Справочная:

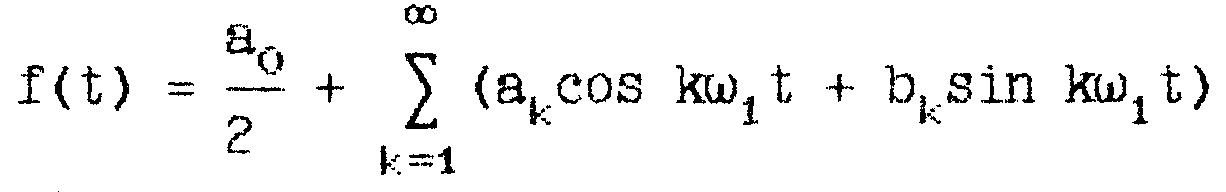
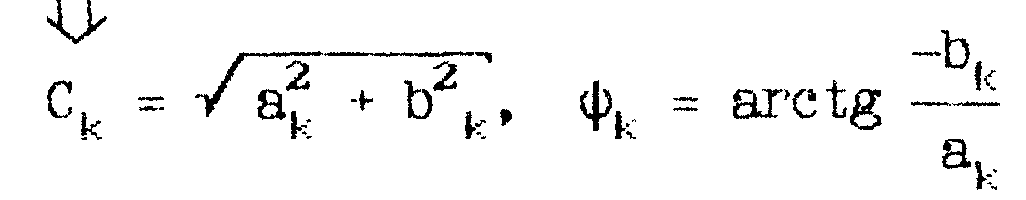
в. Стандартная:

Ряд Фурье можно представить в трех формах:

а. комплексной, которая используется в теоретических выкладках;

б. справочной, которая обычно приводится в справочниках;

в. стандартной, которая используется при практических расчетах.

3. Гармоника с номером k (k - ая гармоника):

С_k - амплитуда.

ф_k - начальная фаза.

k - номер гармоники (k = 0,1,2 ...),

- угловая частота 1-ой гармоники.

4. Пример использования

11.2. Параметры периодических несинусоидальных напряжений

1. Периодическое несинусоидальное напряжение (в стандартной форме записи) ,

2. Амплитудный спектр

а. {U₀, U_1m, U_2m, U_3m,…}

Под амплитудным спектром понимают всю совокупность амплитуд отдельных гармоник. Его наглядно изображают в виде набора отрезков длиною U₀, U_1m, U_2m, U_3m, … , восстановленных к оси частот в точках 0, ω₁, 2ω₂, 3ω₃, ...

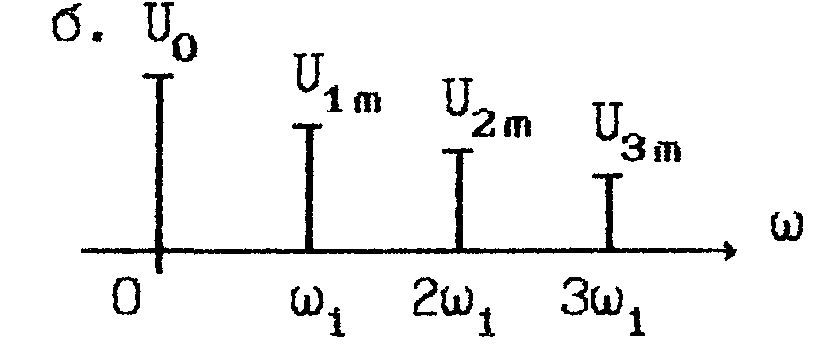
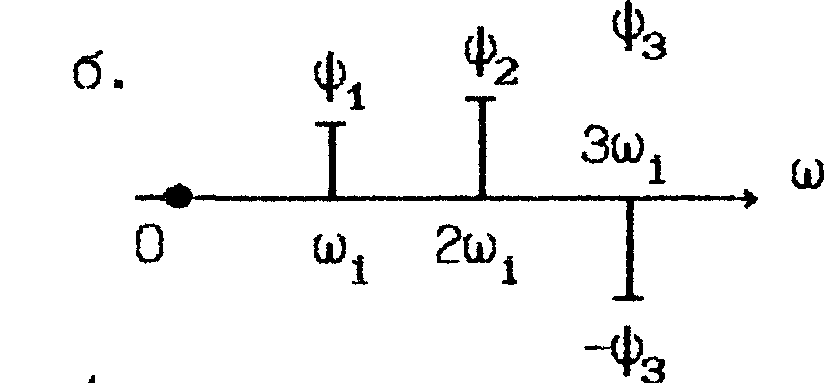
3. Фазовый спектр

a. {0, ₁, ₂, ₃…}

Под фазовым спектром понимают всю совокупность фаз отдельных гармоник. Его наглядно изображают в виде набора линий длиной 0, _1m, _2m, _3m…восстановленных с учетом знака к оси частот в точках ω₁, 2ω₁, 3ω₁,...

Максимальное значение функции U_max равно ординате наиболее удаленной от оси абсцисс точки графика.

Действующее (среднеквадратичное) значение напряжения определяется таким значением постоянного напряжения U, которое будучи приложенным к сопротивлению, вызовет то же самое выделение тепла.

6. 

Коэффициент гармоник определяется отношением среднеквадратичного значения амплитуд высших гармоник к амплитуде первой гармоники.

11.3. Активная мощность в цепи периодического несинусоидального тока

1. Участок цепи

2. Активная мощность, выделяемая на участке цепи

где _k = _k^u - _kⁱ

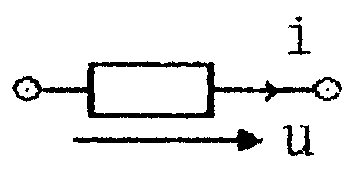
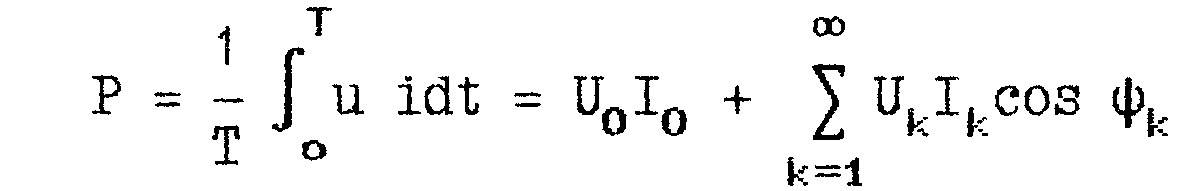
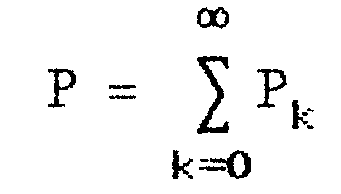
Активная мощность, выделяемая на участке цепи периодического несинусоидального напряжения, равна сумме активных мощностей каждой из гармоник в отдельности.

3. Действующее значение напряжения

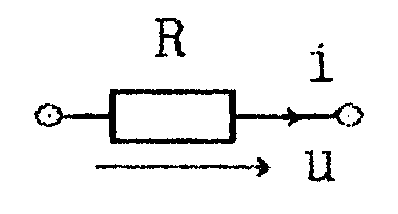
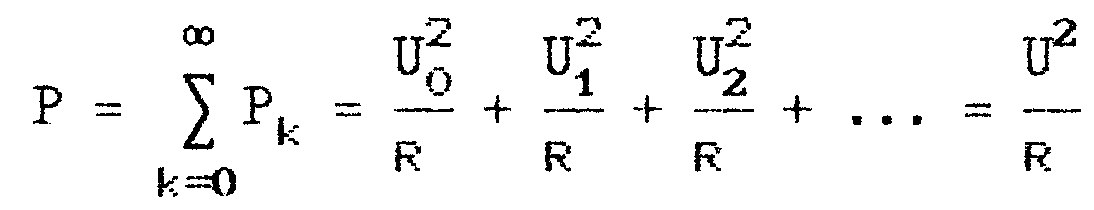
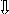
Квадрат действующего значения периодического несинусоидального напряжения равен сумме квадратов действующих значений напряжения отдельных гармоник.

4. Пример использования:

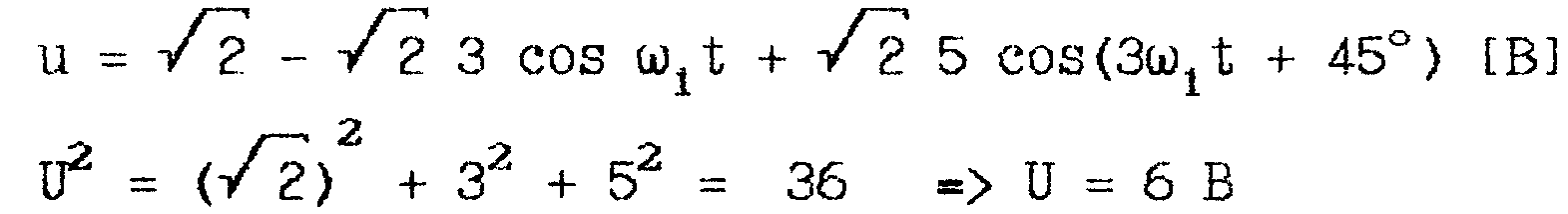
11.4. Расчет цепи периодического несинусоидального тока

1. Постановка задачи расчета

Заданы воздействие и комплексная передаточная функция цепи. Требуется найти реакцию.

2. Расчет реакции осуществляется в 3 этапа:

а. Гармонический анализ или разложение параметров воздействия в ряд Фурье.

П ри этом теоретически бесконечный ряд Фурье "усекают", ограничиваясь первыми четырьмя-пятью гармоникам

б. Расчет реакции для каждой гармоники в отдельности.

в. Гармонический синтез или суммирование результатов расчета гармоник реакции:

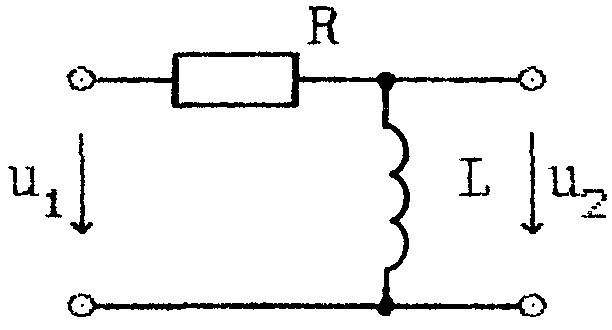
3 . Пример использования (L = 0,1 Гн. R = 10 Ом)

47