лекции_1 / Молекулярка / МКТ

Лекция 11. Молекулярная физика и термодинамика. Молекулярно-кинетическая теория строения вещества. (2 часа)

11.1. Динамические и статистические закономерности в физике. Статистический и термодинамический методы исследования.

11.2. Макроскопическое состояние. Термодинамические функции состояния. Уравнение состояния. Внутренняя энергия. Интенсивные и экстенсивные параметры.

11.3. Модель идеального газа. Основное уравнение состояния идеального газа. Основные газовые законы.

11.4. Молекулярно-кинетический смысл абсолютной температуры.

Демонстрации:

1. Механическая модель броуновского движения.

2. Диффузия в газах, жидкостях и твердых телах.

Видеофильмы:

1. Смешивание спирта с водой - (2 мин.).

2. Броуновское движение - (3 мин.).

МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ВЕЩЕСТВА

Молекулы в атомах, ядро, нейтроны, протоны, электроны неисчерпаемы, как и атом. 80 лет развития физики науки в целом подтвердили предсказание великого философа Цицерона.

Атомной единицей массы называют 1/12 массы атома углерода (С), т. е. удобная величина, численно равная 1,6605655(86)*10^-27.

- количество вещества, 6,02*10²³ штук структурных элементов (неделимых) атомов или молекул.

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

Идеальный газ

Основное уравнение кинетической теории газов

является важнейшим в молекулярно-кинетической теории; из него можно вывести все газовые законы, получить соотношения между энергией молекул и температурой и т.д.

, (11.13)

где n₀ = N^'/V – концентрация молекул - число молекул в единице объема.

Уравнение (11.13) называют основным уравнением молекулярно-кинетической теории газов для давления. Его называют уравнением Клаузиуса. Сделав некоторые преобразования из (11.13) можно получить

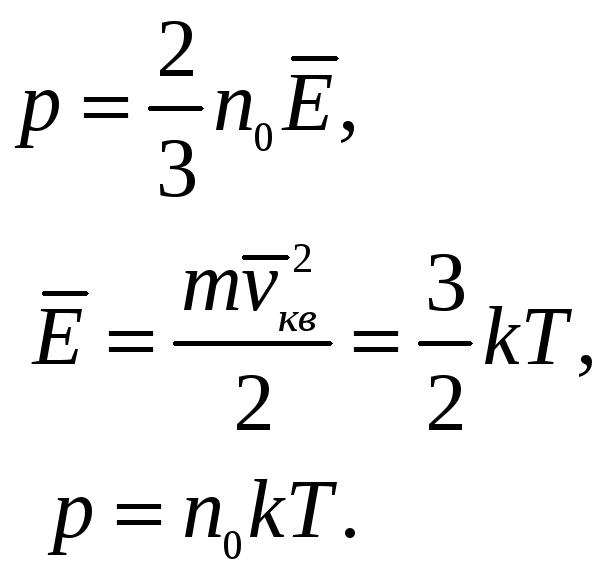(11.14)

где n₀ = N^'/V - число молекул в единице объема;

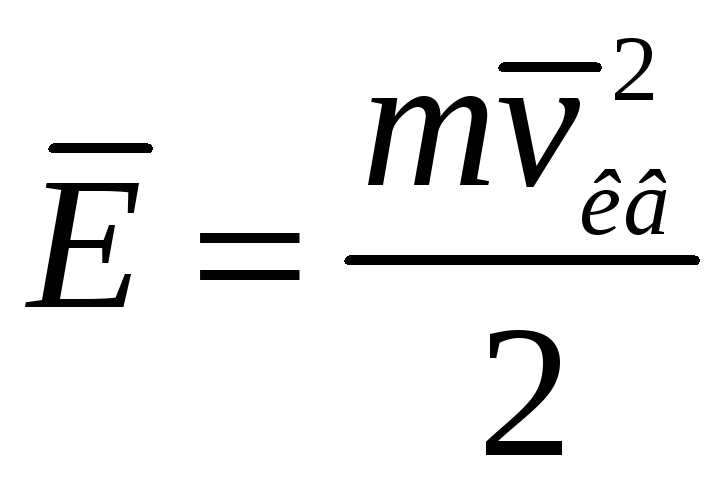=- средняя кинетическая энергия поступательного движения молекул газа;

k - постоянная Больцмана.

ГАЗОВЫЕ ЗАКОНЫ

1. Идеальный газ

- уравнение Клапейрона.

P=P₀=1,013*10⁵ Па;

Т=Т₀=273,15 К;

V=V₀=22,4*10^-3 м³;

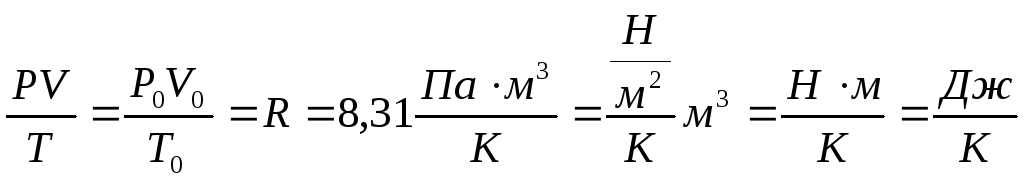
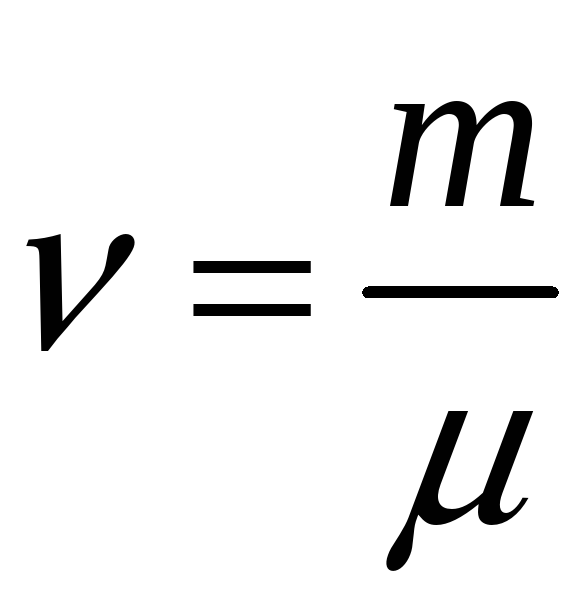
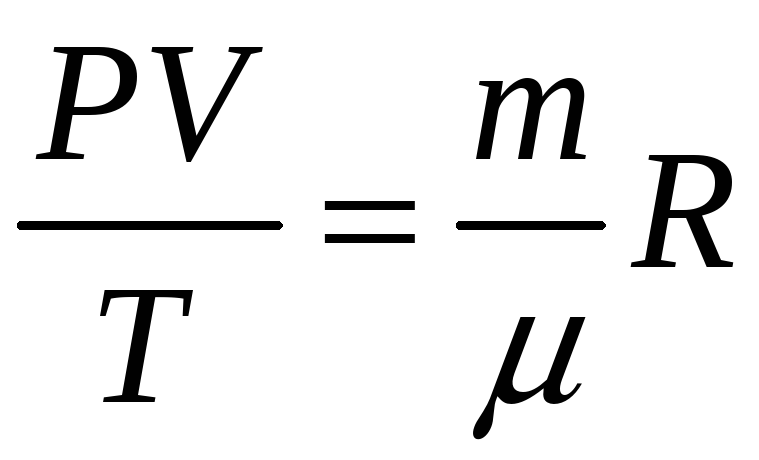
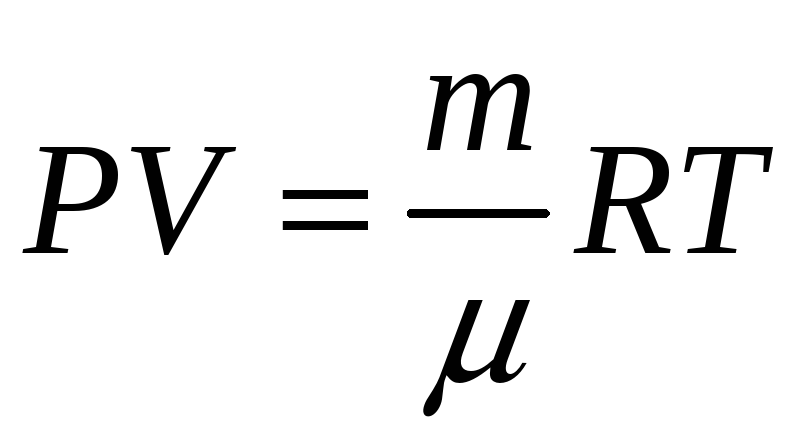- уравнение Менделеева-Клапейрона

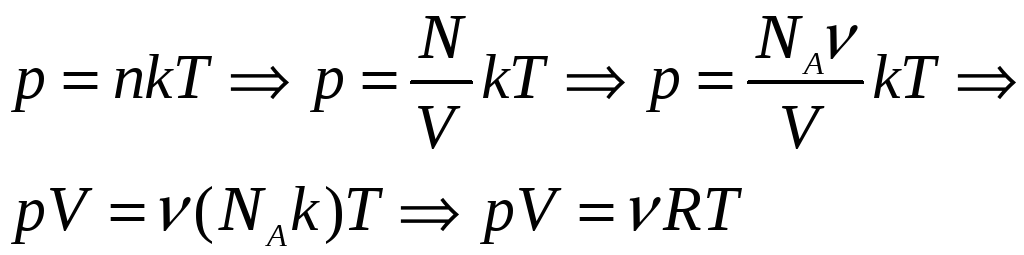
ИЗОПРОЦЕССЫ

1. P=const – изобарный процесс;

:

ЗАКОН ГЕЙ-ЛЮССАКА:

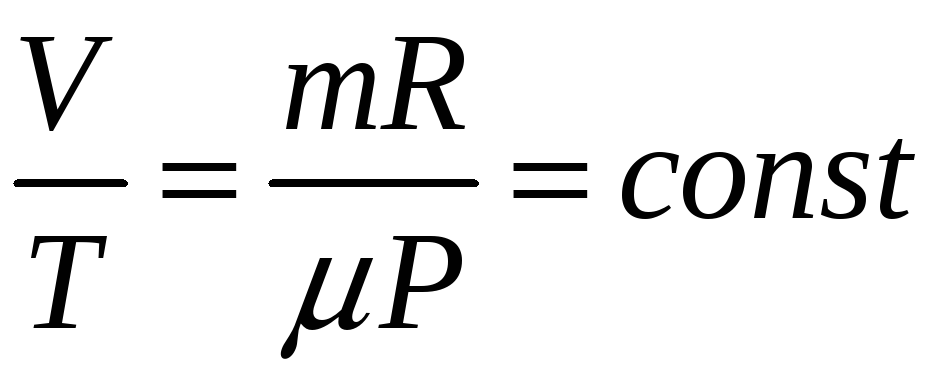
2. T=const – изотермический процесс;

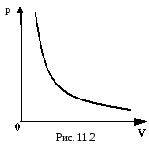
ЗАКОН БОЙЛЯ-МАРИОТТА P

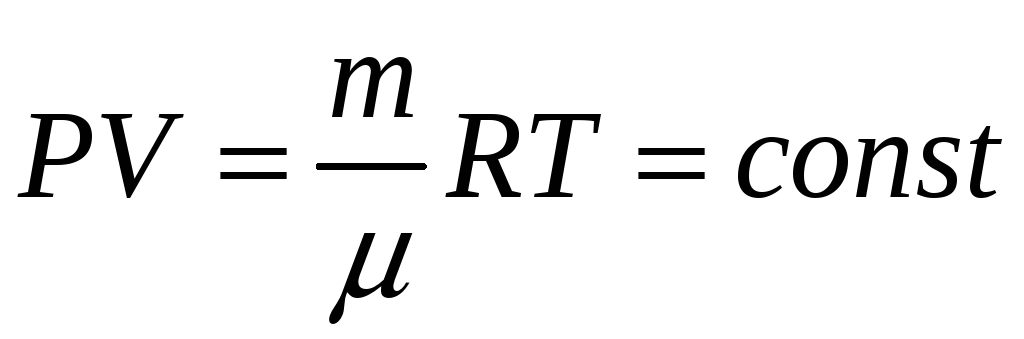
V

3.V=const – изохорный процесс;

ЗАКОН ШАРЛЯ:

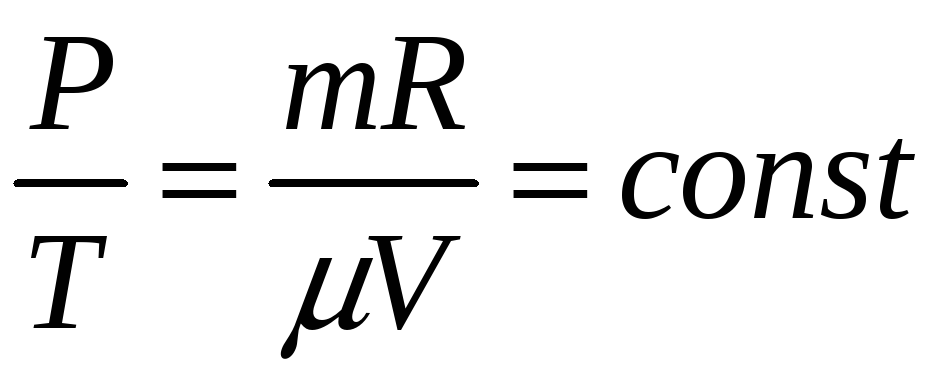
4. Адиабатический процесс;

Адиабатический процесс – процесс, протекающий без теплообмена с внешней средой.

ВЫВОД УРАВНЕНИЯ АДИАБАТЫ

- уравнение адиабаты или уравнение Пуассона.

;

;

.

Адиабата в PV координатах убывает круче, чем изотерма.

PV=const dP*V+P*dV=0 ;

;

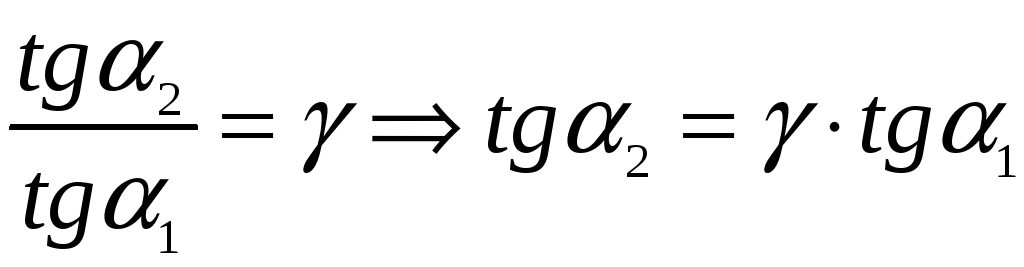
Касательная у адиабаты в раз круче, чем у изотермы.

ПОЛИТРОПИЧЕСКИЙ ПРОЦЕСС

Политропический процесс – это процесс, в ходе которого теплоемкость тела не изменяется. Все рассмотренные нами изопроцессы можно представить себе, как политропические.

Изопроцессы – частные случаи политропического процесса.

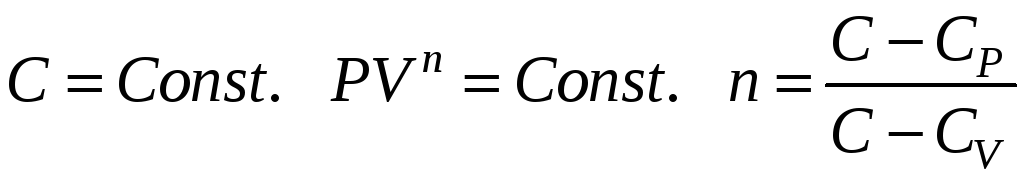
1. n=0 PV⁰=P*1=P=const;

- изобарический процесс.

2. PVⁿ=const

, , , 1*V=const, V=const – изохорический процесс.

3. n=1 PV=const – изотермический процесс.

4. n= - адиабатический процесс.

РАБОТА ИДЕАЛЬНОГО ГАЗА В ИЗОПРОЦЕССАХ

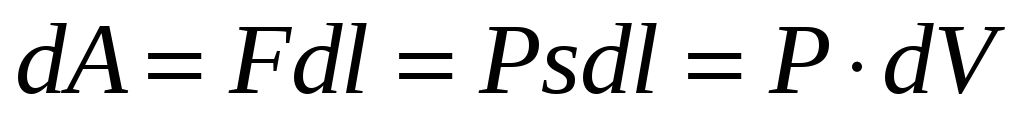
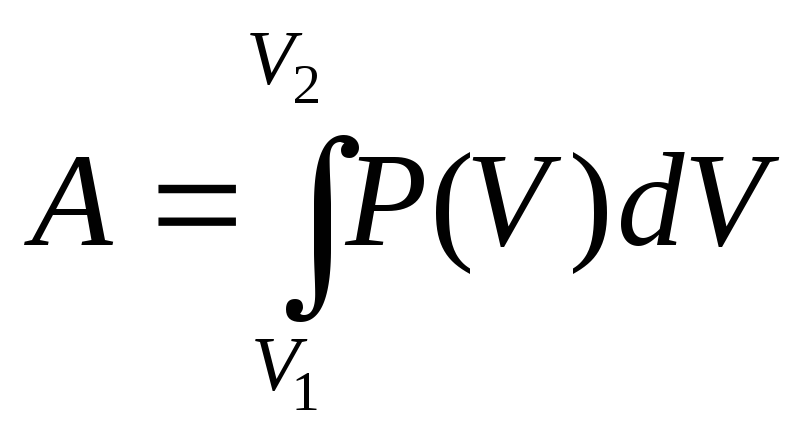
1. V=const – изохорический процесс

dA=PdV=0

2. P=const – изобарический процесс

A=P(V₂-V₁)

3. T=const – изотермический процесс

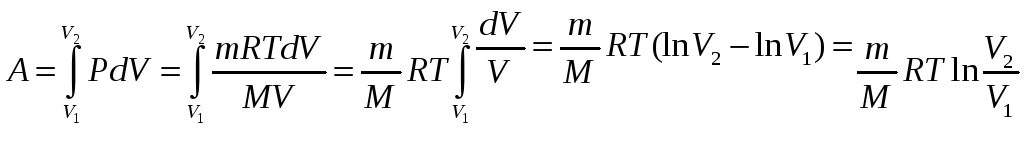
4. адиабатический процесс

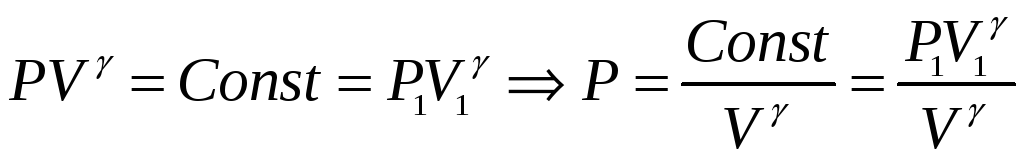
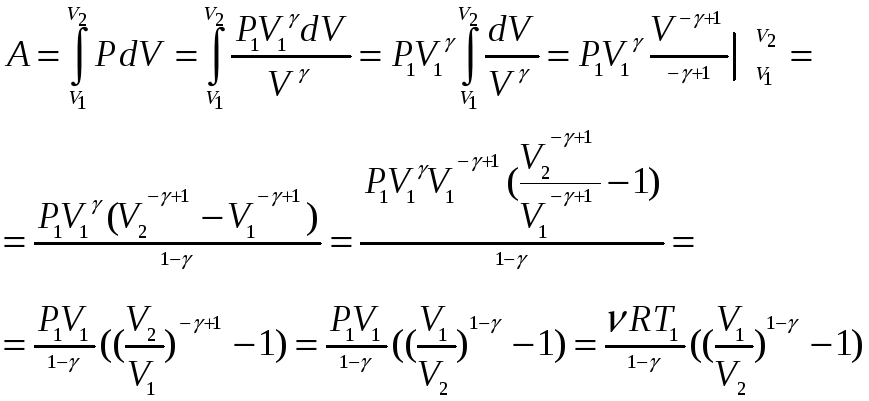
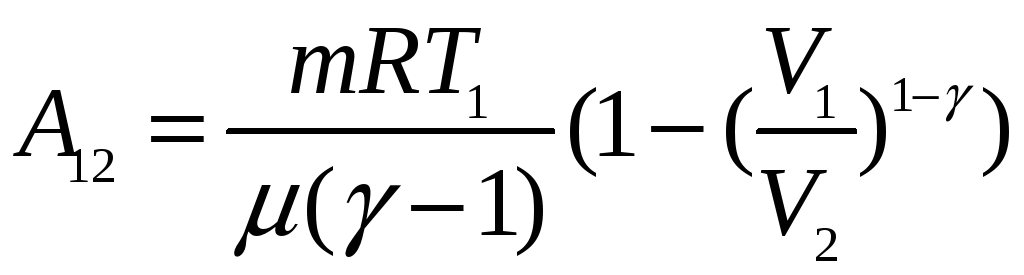
5. политропический процесс

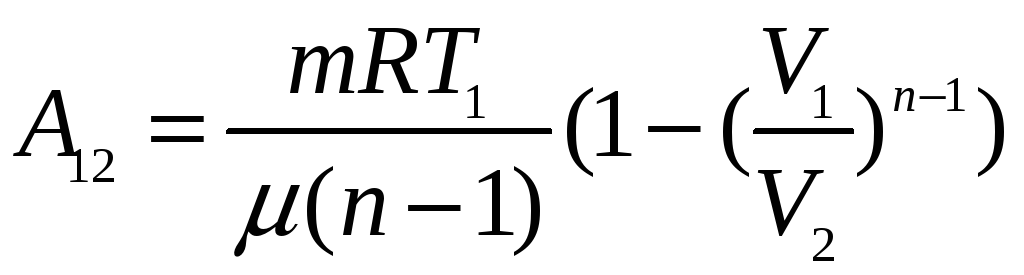
ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА

dQ=dU+dA

Теплоемкость тела - физическая величина равная производной от количества тепла по температуре.

C=dQ/dT

Для газа различают в зависимости от условий, в котором происходит нагрев газа следующую теплоемкость.

1. P=const Cp 2. V=const Cv

Для жидких и твердых тел теплоёмкость одинакова.

Теплоёмкость различают по количеству вещества:

1 - молярная теплоёмкость;

2 – удельная теплоемкость.

dQ=CdV

dQ=CvUdT, U - количество вещества;

dQ=CvMdT, M - масса вещества.

РАССМОТРИМ ДВА СЛУЧАЯ НАГРЕВАНИЯ ГАЗА.

1. При V=const C=Cv

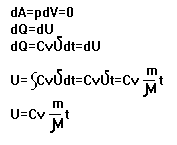
2 . При P=const C=Cp

Молярная теплоёмкость газа при постоянном давлении равно сумме молярной теплоёмкости при постоянном объеме плюс универсальная газовая постоянная.

Cp > Cv ==> Сp = Cv + P - Закон Майера

Количество теплоты, которое нужно подвести к газу при постоянном давлении больше чем при постоянном объеме связано это с тем что при постоянном давлении часть теплоты передаваемой газу переходит не во внутреннюю энергию, а идет на совершение работы при расширении газа.

Для идеального газа внутренняя энергия складывается исключительно из кинетической энергии поступательного движения бесконечно малых молекул идеального газа.

U=NWk, где N - число молекул.

Число степеней свободы механической системы - это количество независимых координат, с помощью которых может быть задано положение системы в пространстве. Если молекула рассматривается как бесконечно малый шарик, то её положение в пространстве задается координатами (x , y , z).

i - степень свободы.

Если молекула двухатомная, то i=5 , помимо трех координат поступательного движения эту молекулу будут определять еще две координаты вращательного движения.

Если же от идеального газа мы переходим к реальному газу, то есть, учитываем конечные размеры молекул или учитываем, что молекулы взаимодействуют дуг с другом, то к внутренней кинетической энергии поступательного или вращательного движения нужно добавить энергию взаимодействия молекул или энергию колебательного движения.

ЗАКОН О РАВНОРАСПРЕДЕЛЕНИИ ЭНЕРГИИ МОЛЕКУЛ ПО СТЕПЕНЯМ СВОБОДЫ:

1. На каждую степень свободы приходится одинаковая энергия равная 1/2 KT: