10.3. Учет слабой заполненности матриц
Наиболее эффективный способ экономии памяти и вре- мени ЭВМ при расчете установившегося режима - это учет слабой заполненности матрицы Yу.
Линейные алгебраические уравнения, встречающиеся при решении задачи расчета установившихся режимов, имеют следующие особенности:
матрица коэффициентов системы симметричная;
в подавляющем большинстве случаев матрица коэффи- циентов системы уравнения является слабо заполненной или разреженной - содержит большое число нулевых эле- ментов, расположение которых произвольно.
Если узлы k и j соединены непосредственно друг с другом, то взаимная проводимость Ykj равна нулю. В сложных электрических системах узел k соединен не со всеми остальными узлами, а лишь с некоторыми из них. Поэтому большинство взаимных проводимостей (элементов матрицы Yу) равно нулю. Так, число ненулевых элементов в матрице узловых проводимостей для схем замещения сложных электрических систем с большим количеством уз- лов п составляет примерно 4n, т. е. п2- 4п элементов этой матрицы равны нулю [18].
Непосредственное применение стандартных программ решения систем линейных уравнений в расчетах установив- шихся режимов нецелесообразно. Эффективность расчетов сильно повышается, если учитывать наличие нулевых эле- ментов в матрице Yу. В этом случае, с одной стороны, эко- номится память ЭВМ, так как запоминаются лишь нену- левые элементы матрицы Yу, с другой стороны, уменьша- ется количество выполняемых операций, так как не производятся арифметические действия с нулевыми элемен- тами. Ни одна современная программа расчета установив- шегося режима на ЭВМ, использующая методы Гаусса, Ньютона или Зейделя, не может быть эффективна, если в ней не предусмотрен учет слабой заполненности матриц коэффициентов.
Учет
слабой заполненности Yу
осуществляется алгорит-
мически
очень просто при применении метода
Зейделя (или
простой
итерации). Для этого надо при вычислении
(i+
+1)-го
приближения напряжения k-го
узла
по вы-
ражению
(9.40) выполнять
арифметические действия лишь
с
не равными нулю взаимными проводимостями
узлов. Это
легко
сделать, используя информацию о топологии
сети,
т.
е. о том, с какими узлами соединен узел
k.
Учет ненулевых элементов при решении уравнений уста- новившегося режима точными методами более сложен. В этом случае надо использовать, например, метод Гаусса при заполнении и обработке только ненулевых элементов. Однако в процессе исключения неизвестных методом Гаус- са появляются новые ненулевые элементы, отсутствовав- шие в исходной матрице.
Заранее трудно предусмотреть, сколько новых ненуле- вых элементов появится при реализации метода Гаусса. Именно поэтому требуемый для расчета установившегося режима объем памяти ЭВМ не может быть выражен толь- ко через число узлов электрической системы, важно и рас- положение ненулевых элементов1.
Фактически задача учета слабой заполненности сводит- ся к такой записи уравнений установившегося режима,
Рис. 10.9. Нумерация узлов, приводящая матрицу присоединения узлов к ленточной форме:
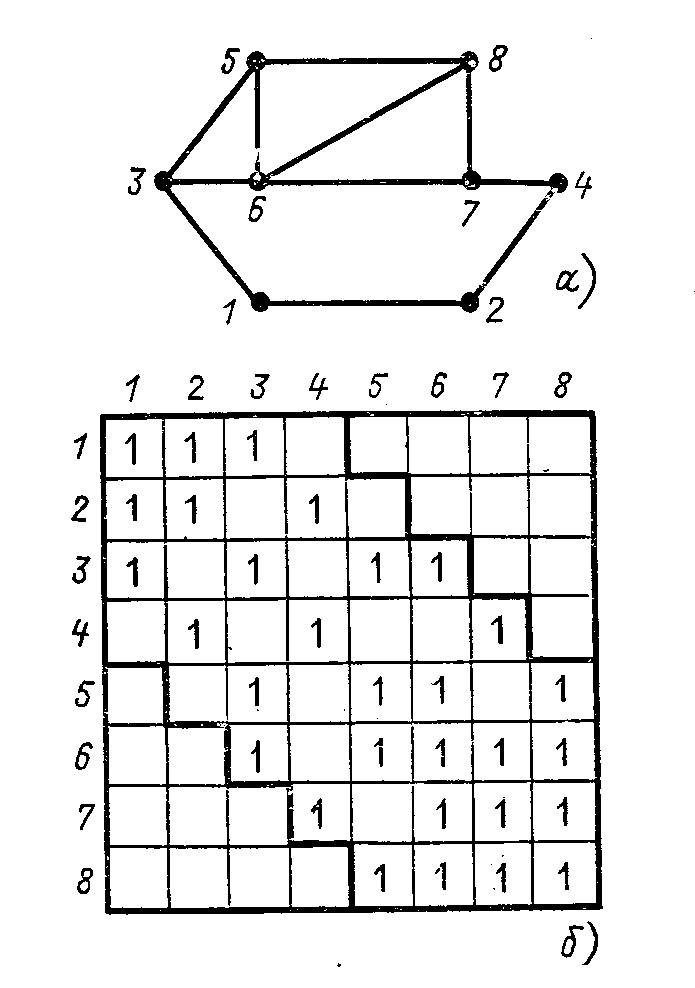а
- граф сети;
б - матрица присоединения
при которой ненулевые элементы матрицы узло- вых проводимостей будут сгруппированы так, чтобы в ходе решения системы линейных уравнений по- явилось как можно мень- ше новых ненулевых эле- ментов.
Расположение ненуле- вых элементов матрицы Yу определяется способом нумерации узлов схемы электрической системы. Это легко проиллюстриро- вать с помощью матри- цы присоединения узлов. Элементы квадратной матрицы присоединения узлов состоят из нулей и единиц (для приводимых ниже рассуждений знак элемента матрицы не имеет значения). Если узел k соединен с узлом j (т. е. Ykj0), то на пересечении k-й строки и j-го столбца будет единица.
На диагонали матрицы присоединения узлов находятся единицы. Иными словами, матрица присоединения узлов отличается от матрицы Yу тем, что все ненулевые элементы Yу заменены единицами.
Наиболее простой и достаточно эффективный при при- менении метода Гаусса способ нумерации узлов состоит в приведении матрицы присоединения узлов к ленточной форме. Матрицей в ленточной форме называют такую, у ко- торой ненулевые элементы расположены в виде «ленты» вдоль главной диагонали матрицы (рис. 10.9). Такая фор- ма записи матрицы Yу эффективна для сетей цепочечной или близкой к ней структуры [20]. Покажем, как прону- меровать узлы, чтобы привести матрицу присоединения к ленточной форме.
Будем называть степенью узла1 число ветвей, присоеди- ненных к этому узлу [20]. Первый номер присвоим узлу с минимальной степенью. Если таких узлов несколько, вы- бираем любой из них. Далее, в порядке возрастания номе- ров уже пронумерованных узлов нумеруем смежные с ни- ми непронумерованные узлы, причем нумерация ведется в порядке возрастания их степеней.
Этот способ нумерации легко реализовать на ЭВМ. Для каждого узла подсчитывается степень, т. е. число других узлов, с которыми он соединен. Узлы нумеруются в соответ- ствии со степенями. Номер узла тем больше, чем с боль- шим количеством других узлов он соединен [19, 20]. Такой способ нумерации узлов приводит к существенному сокра- щению числа новых ненулевых элементов, возникающих в процессе исключения по Гауссу.
Существуют многочисленные способы нумерации уз- лов и учета слабой заполненности матрицы Yу. Используя методы теории графов, можно с помощью специальных алгоритмов определять оптимальную с точки зрения эко- номии памяти и уменьшения числа операций нумерацию узлов. В то же время простые способы нумерации узлов, например приведенный выше, достаточно эффективны и их усложнение часто нецелесообразно. Еще раз подчеркнем, что возможность учета слабой заполненности матрицы Yу составляет важнейшее преимущество методов Гаусса и Ньютона при решении линейных и нелинейных уравне- ний установившегося режима в сравнении с методами, ис- пользующими матрицу собственных и взаимных сопротив- лений узлов, в которой нет нулевых элементов.
Рассматриваемые ниже способы эквивалентирования и разделения электрических систем на подсистемы эффек- тивны в сочетании с учетом слабой заполненности матриц.