Расчет вероятностей блокировок многозвенных коммутационных схем по методу графов Ли

1. Цель практической работы:

Ознакомление с подходом к оценке вероятностей блокировок многозвенных коммутационных схем по методу графов Ли.

Перед выполнением лабораторно-практических заданий студенты должны ориентироваться в основных аспектах теории вероятностей, графов, теории массового обслуживания на примерах систем с отказами и с очередями, обладать навыками программирования и функционального моделирования в программных средах MathCad/ Matlab (пакет Simulink)/LabVIEW.

В результате выполнения практического задания студенты должны освоить принципы определения вероятностей блокировок многозвенных коммутационных схем по методу графов Ли и анализа характера их зависимостей в программных средах MathCad/ Matlab (пакет Simulink)/ LabVIEW.

2.2. Краткие теоретические сведения

Для сокращения числа точек коммутации применяются схемы с двумя и более звеньями.

Даже для трехзвенных коммутационных схем большой емкости число точек коммутации может быть недопустимо большим.

В этом случае наиболее существенное уменьшение числа точек коммутации может быть достигнуто не столько за счет введения дополнительных звеньев в коммутационную схему, сколько за счет работы коммутационной схемы с приемлемо малым значением вероятности блокировки.

Одним из наиболее гибких и логически простых методов вычисления вероятности блокировок является метод, основанный на использовании вероятностных графов, предложенный Ли [4].

Если какая-либо одна из группы n параллельных линий может быть использована при установлении соединения, то полная вероятность блокировки В есть вероятность того, что все n линий заняты:

В = рⁿ ,

где р – вероятность того, что линия занята.

Если при установлении соединения необходимо использовать n последовательно соединенных линий, то вероятность блокировки определяется как:

B=1–qⁿ, (2.1)

где q=1–р – вероятность того, что линия свободна.

Вероятностный граф трехзвенной коммутационной схемы изображен на рис. 2.1 и показывает, что любое соединение может быть установлено k различными путями: каждый путь проходит через один коммутатор центрального звена.

Вероятность того, что любая промежуточная линия занята, обозначается через p₁.

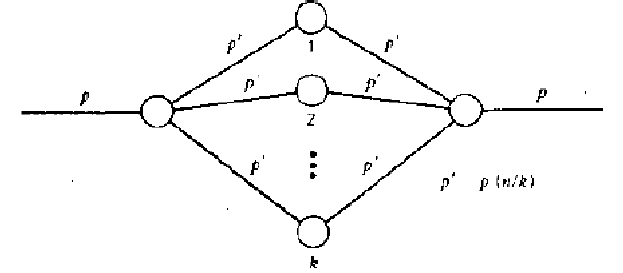
Рис. 2.1 Вероятностный граф трехзвенной коммутационной схемы

Вероятность блокировки трехзвенной схемы может быть определена

как:

В = (1-(q₁)²)^k , (2.2)

где k – число коммутаторов центрального звена, и q₁ = 1 - p₁ – вероятность того, что промежуточная линия свободна.

Если известна вероятность р того, что занят вход, то вероятность p₁ того, что занята промежуточная линия, можно определить как:

p₁ = p/β, (2.3)

где β = k/n – коэффициент расширения.

Это выражение показывает, что, если занято некоторое число входов, то также занято такое же число выходов из коммутатора первого звена.

Величина β определяется на основе допущения, что k больше n: это означает, что на первом звене коммутационной схемы имеет место пространственное расширение. Если же β меньше 1, то это означает, что на первом звене осуществляется концентрация поступающей нагрузки.

Окончательная формула для вероятности блокировки трехзвенной коммутационной схемы, выраженная через использование входящих линий р:

В = [1- (1- p / β)²] · k . (2.4)

Если средние три звена пятизвенной коммутационной схемы являются строго неблокирующимися (k₂ = 2·n₂ - 1), то такая структура позволяет получить экономию точек коммутации на каждом коммутаторе центрального звена рассмотренной ранее трехзвенной коммутационной схемы.

Вероятностный граф пятизвенной схемы приведен на рис. 2.2 (см. ниже). На основе этого графа вероятность блокировки может быть оценена следующим образом:

B = {1-(q₁)²·[1-(1- q₂²) ^k2 ]}^k1, (2.5)

где q₁ = 1 – p₁ и q₂ = 1 – p₂ .

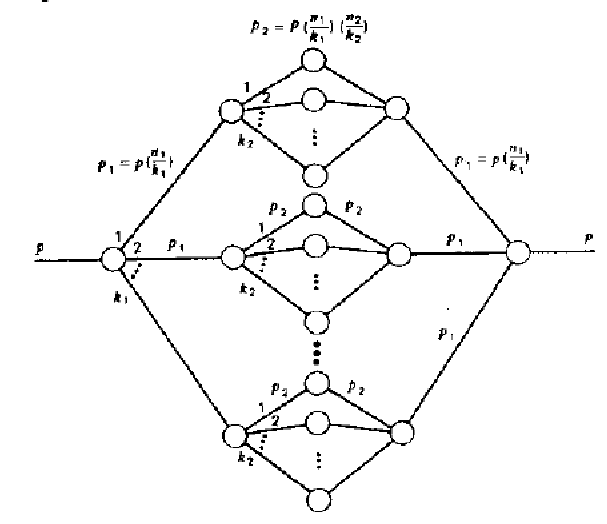
Рис. 2.2. Вероятностный граф пятизвенной коммутационной схемы

3. Практическое задание

1. На основе использования соответствующей математической модели рассчитать и построить зависимости вероятности блокировок по методу Ли для трехзвенной коммутационной схемы от емкости системы.

2. Рассчитать и построить зависимости вероятности блокировок по методу Ли для трехзвенной коммутационной схемы от коэффициента пространственного расширения/концентрации (β < 1 и β ≥ 1).

3. Рассчитать и построить зависимости вероятности блокировок по методу Ли для трехзвенной коммутационной схемы от загрузки входящей линии (0,1 < р < 0,8).