12.3. Распределение Больцмана. Барометрическая формула

Атмосферное давление на какой-либо высоте обусловлено весом вышележащих слоев газа.

Если давление газа на высоте h_o равно p_o, а высоте h - p, то разность давлений с изменением высоты на

или но = m/V, а pV = (m/)RT, т.е.  = p/RT, тогда

. (12.17)

При T = const, будем иметь

или (12.18)

но при h = 0, p = p₀, C = p₀, следовательно

(12.19)

Полученное соотношение называютбарометрической формулой, которая показывает, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура (рис.12.3).

Из молекулярно-кинетической теории известно, что следовательно

Заменив в барометрической формуле значения давлений, на число молекул в единице объема, с учетом того, что /R = m/k, получим

(12.20)

Формула (12.20)определяет закон распределения молекул газа по высоте в поле сил тяготения.

Так как mgh = W_p (потенциальная энергия молекул в поле сил тяготения), то

(12.21)

где n_o - число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю;

n - число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна W_p.

Из полученной формулы видно, что с понижением температуры, число молекул на высотах h не равных нулю, убывает и при T0, оно равно нулю. Таким образом, при температуре T = 0 все молекулы газа расположились бы у поверхности Земли. При T, n слабо убывает с высотой, так что все молекулы оказываются почти равномерно распределенными по высоте. Молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия, и, наоборот, с меньшей плотностью там, где их потенциальная энергия больше. Отсюда

; , (12.22)

где m_o - масса одной молекулы.

Больцман показал, что такое распределение молекул справедливо не только в случае потенциального поля тяготения Земли, но и в любом силовом потенциальном поле. Это распределение и называют распределением Больцмана, которое дает распределение частиц по значениям потенциальной энергии.

Распределение частиц по значениям потенциальной энергии было использовано Перреном для экспериментального определения числа Авогадро.

12.4. Внутренняя энергия и теплоемкости идеального газа. Классическая теория теплоемкостей

Внутренняя энергия тела равна сумме кинетической энергии поступательного и вращательного движения молекул этого тела, и потенциальной энергии их взаимного расположения

. (12.23)

Внутренняя энергия газа складывается из энергии отдельных молекул. В одном киломоле любого газа содержится N_А молекул (N_А - число Авогадро). Следовательно, один киломоль идеального газа имеет внутреннюю энергию, равную

(12.24)

Внутренняя энергия произвольной массы газа m

(12.25)

где  - молярная масса газа.

Таким образом, внутренняя энергия идеального газа зависит только от его объёма и давления.

Пользуясь понятием внутренней энергии газа, найдём выражение для его теплоёмкостей.

Теплоемкость это физическая величина, численно равная количеству теплоты, которое необходимо сообщить веществу для нагревания его на один градус.

Удельной теплоёмкостью "c" газа называется физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы газа для нагревания её на один градус.

Кроме удельной теплоёмкости для газов вводится понятие молярной теплоёмкости.

Молярной теплоёмкостью "C" называется физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю газа, чтобы увеличить его температуру на один градус

(12.26)

Для газов вводятся в рассмотрение молярные теплоемкости при постоянном объёме "C_v" и при постоянном давлении "C_p".

Если газ нагревается при постоянном объёме, то подводимое к газу тепло идёт на увеличение его внутренней энергии. Следовательно, в этом случае изменение внутренней энергии газа при нагревании его на один градус будет равно молярной теплоёмкости

, т.е. (12.27)

Таким образом, для определения C_v необходимо знать число степеней свободы молекул газа.

При нагревании одного моля газа в условиях постоянного давления сообщаемое ему извне тепло идёт не только на увеличение его внутренней энергии, но и на совершение работы против внешних сил. Следовательно,

(12.28)

Работа, совершаемая по свободному расширению одного моля газа в цилиндре под поршнем равна

(12.29)

где S h = V - увеличение первоначального объёма при нагревании газа на один градус (V = V₂ - V₁).

На основании уравнения Менделеева - Клапейрона для одного моля идеального газа .

В нашем случае, где T₂ = T₁ + 1, т.е. откудаТогда, следовательно

или . (12.30)

Так как c_p = c_v + R/, то

. (12.31)

Очень часто для характеристики газа пользуются отношением

. (12.32)

Согласно многочисленным исследованиям по определению C_p, и C_v между теорией и экспериментом для одноатомных и двухатомных молекул имеется удовлетворительное совпадение. Согласно рассмотренной нами теории теплоёмкости газов должны быть целыми и кратными R/2. Однако, между теоретическими и экспериментальными данными имеется определённое расхождение.

О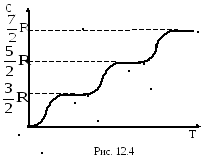собенно большие расхождения между теорией и экспериментом наблюдаются при рассмотрении температурной зависимости теплоёмкости. Согласно изложенной теории теплоёмкость не должна зависеть от температуры; на самом же деле это оказывается справедливым только в определённых интервалах температур, при этом, в различных интервалах теплоёмкость имеет значения, соответствующее различному числу степеней свободы (рис.12.4, 12.5).

Это связано с тем, что число степеней свободы одного и того же газа изменяется с изменением температуры. При низких температурах молекулы газа обладают только поступательными степенями свободы, при средних температурах - поступательными и вращательными степенями свободы, а при высоких температурах - поступательными, вращательными и колебательными степенями свободы. При этом, переход от одного числа степеней свободы к их другому числу осуществляется скачкообразно. Изменение числа степеней свободы приводит к изменению теплоемкостей газа. Такое поведение теплоёмкостей объясняется квантовой теорией. Согласно этому объяснению энергия вращательного и колебательного движений изменяются скачкообразно - квантуется, а энергия поступательного движения нет.

Молекулы газа, вернее подавляющая их часть, имеют энергию близкую по своему значению к средней кинетической энергии поступательного движения (<Е_к>). Незначительная часть их имеет энергию, значительно превышающую <Е_к>. При низких температурах молекулы газа практически движутся поступательно, поэтому теплоёмкость газа равна 3R/2.

Повышение температуры сопровождается увеличением <Е_к> в результате чего всё большее и большее число молекул вовлекается во вращательное движение и при некоторой температуре, (вернее, в определённом интервале температур) все молекулы будут вращаться. Это соответствует увеличению их теплоёмкости до 5R/2. Наконец, при дальнейшем увеличении температуры часть молекул начинает совершать колебательное движение, в связи, с чем теплоёмкость станет равной 7R/2.

Таким образом, классическая теория теплоёмкостей верна только для отдельных температурных интервалов, при этом, каждому интервалу соответствует своё число степеней свободы.

Формулы кинетической энергии молекул газа и молярных теплоемкостей в классической теории теплоемкости, основанной на теореме Больцмана о равномерном распределении энергии по степеням свободы, представлены в таблицах 12.1 и 12.2.