12.2. Вероятность и флюктуации. Распределение молекул (частиц) по абсолютным значениям скорости. Распределение Максвелла. Скорости теплового движения частиц. Средняя длина свободного пробега молекул

Статистическая физика это раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующиеся средними величинами.

Статистические закономерности - количественные закономерности, устанавливаемые статистическим методом, в котором рассматриваются лишь средние значения величин, характеризующих данную совокупность молекул (рассматривается конкретная молекулярная модель и к ней, применяются математические методы статистики, основанные на теории вероятностей).

Одними из основных понятий статистической физики являются: вероятность и флуктуации.

Вероятность это число способов, которыми может быть реализовано данное состояние макроскопической физической системы (предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях):

w = n/N, (12.3)

где N - число опытов;

n - число раз получено определенное событие.

Флуктуации это случайные отклонения физических величин от их среднего значения.

Согласно молекулярно-кинетической теории молекулы идеального газа находятся в непрерывном хаотическом движении с равномерным распределением по направлениям. Скорости молекул при этом изменяются по величине. Наиболее близкой к истинному значению скорости является средняя квадратичная скорость молекул, которая для газа массой "m" находящегося в состоянии равновесия, при T = const, остаётся постоянной

или , (12.4)

где N_i - число молекул, обладающих скоростью v_i;

N - число всех молекул.

Рассчитаем среднюю квадратичную скорость молекул воздуха при температуре 300К (27⁰С). Будем считать, что воздух состоит из молекул азота (N₂) с молярной массой 28 кг/кмоль, тогда

м/с.

Постоянство <v_кв> объясняется тем, что в стационарном состоянии газа устанавливается стационарное распределение молекул по скоростям, подчиняющееся статистическому закону Максвелла.

Этот закон указывает на существование некоторой наиболее вероятной скорости движения молекул, в окрестности, которой в интервале (v + dv) находится большее число молекул, чем в окрестности другой скорости.

Возможные скорости движения молекул, заключенные в пределах от нуля до бесконечности, не равновероятны. Слишком большие по сравнению со средним квадратичным значением скорости могут реализоваться крайне редко, т.к. для этого должно реализоваться маловероятное явление, когда в результате случайных столкновений молекулы полностью передадут свою энергию одной (или нескольким) молекуле. Точно также практически исключено, что в результате соударений скорость молекулы станет равной нулю. Следовательно, очень малые и очень большие по сравнению со средним значением скорости маловероятны.

Из сказанного следует, что скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения. Впервые функцию распределения молекул по скоростям получил Максвелл в 1860г. Мы воспользуемся готовым результатом и проанализируем его.

Пусть - общее число молекул, заполняющих сосуд,- число молекул, скорости которых заключены в интервале отv до v+dv. Естественно считать, что прямо пропорционально общему числу частици ширине интервала скоростейdv, т.е.

(12.5)

При этом коэффициент пропорциональности  должен зависеть от v, т.е. = f(v). Максвелл получил

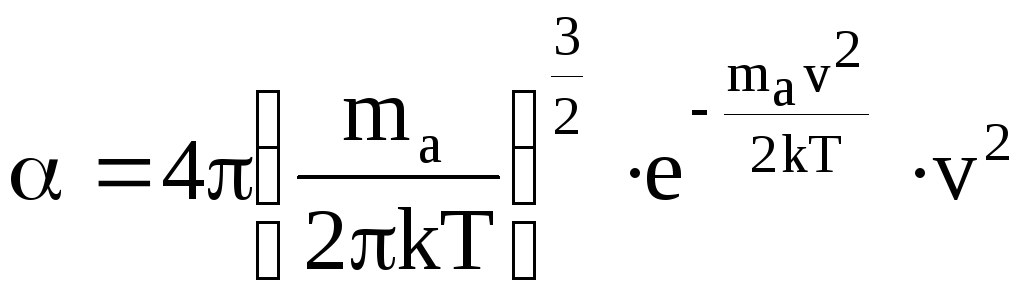. (12.6)

Подставляя (12.6) в (12.5) и разделив, обе части равенства, на dv получим

. (12.7)

На рисунке 12.1 приведен график зависимостидля двух температур.

Проанализируем эту зависимость. Зависимость имеет выраженный максимум, в точке v = v_н. Значение v_н называют наивероятнейшей скоростью. Если выделить три одинаковых по ширине интервала скоростей в области малых скоростей, в окрестности наивероятнейшей скорости и в области больших скоростей, как показано на рисунке, то можно сделать следующие выводы:

1. Число молекул, имеющих малые скорости, относительно мало.

2. Число молекул, имеющих очень большие скорости, относительно мало.

3. Большая часть молекул движется со скоростями, близкими к наивероятнейшей.

Неожиданным оказывается ответ на вопрос - сколько же молекул имеют вполне определенное значение скорости, например, имеют наивероятнейшую скорость? Ответ – нисколько, нуль !!! Действительно, поскольку ширина заданного интервала скоростей равна нулю, то площадь соответствующей полоски на графике также равна нулю. Т. е., в большой массе молекул, в данное мгновение может не найтись ни одной молекулы, имеющей скорость с точно заданным значением.

Найдем значение наивероятнейшей скорости, для чего исследуем функцию на экстремум. Возьмем от функции dN/dv производную по v и приравняем ее нулю: . Для упрощения операции обозначим постоянный множитель буквой А, т.е.

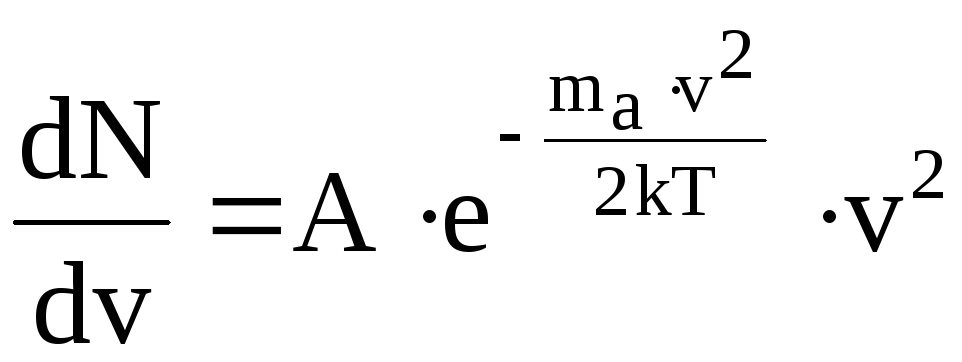. (12.8)

Тогда

(12.9)

Откуда

. (12.10)

Таким образом, получаем .

Из выражений (12.10) видно, что с повышением температуры Т максимум исследуемой зависимости смещается вправо (рис. 12.1). Вместе с тем максимум становится ниже. Это объясняется просто: если максимум сместился вправо, то кривая становится шире, но площадь фигуры, образованной кривойи осью «O - v» – должна быть одинаковой при Т₁ и T₂, т.к. указанные площади численно равны одной и той же величине - числу молекул внутри сосуда. Поэтому максимум для кривой при T₂ должен быть ниже чем максимум этой кривой для Т₁.

По своему численному значению наивероятнейшая скорость близка к средней квадратичной скорости, характеризуется аналогичной зависимостью от температуры.

Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d. Эффективный диаметр несколько уменьшается при увеличении скорости молекул, т. е. с повышением температуры. Величина называетсяэффективным сечением молекулы.

Средний путь, проходимый молекулой между двумя последовательными столкновениями, называется средней длиной свободного пробега .

За 1 с молекула проходит в среднем путь, равный средней скорости . Если за 1 с в среднем происходитстолкновений, то средняя длина пробега

. (12.11)

Предположим, что все молекулы, кроме данной молекулы, застыли неподвижно на своих местах (рис. 12.2).

Столкновение происходит в том случае, если центр молекулы, с которой сталкивается данная молекула, лежит внутри цилиндра радиуса d. За 1 с данная молекула столкнется с неподвижными молекулами столько раз, сколько находится внутри такого цилиндра длиной l = │v│∙1 c. Объем этого цилиндра составляет V = ; число молекул, заключенных в немN = (n – концентрация), следовательно, число столкновений

. (12.12)

В действительности все молекулы движутся, вследствие чего число соударений определяется средней скоростью движения молекул по отношению друг к другу. Как показывает расчет, средняя скорость относительного движения молекул в раз больше │v│ (относительно стенок сосуда). Поэтому

(12.13)

Подставляя (12.13) в (12.11), получим

или . (12.14)

Поскольку, при постоянной температуре, n изменяется пропорционально p (p = n∙k∙T), то

(12.15)

Так, например, при нормальных условиях n = 2,6810²⁵ м ˉ³, эффективный диаметр молекулы ~1 Å = 10^-10 м, поэтому длина свободного пробега ₀ = 210^-7 м, а при давлении 0,1 Па 0,10 м.

Учёт взаимодействия между молекулами показывает, что при возрастании температуры средняя длина свободного пробега несколько увеличивается. Средняя длина свободного пробега при какой-то температуре Т может быть определена по формуле

(12.16)

где C - постоянная Сезерленда, зависящая от интенсивности молекулярных взаимодействий.

<_o>- длина свободного пробега молекул без учёта их взаимодействий.

Средняя длина свободного пробега молекул играет большую роль при молекулярно-кинетическом объяснении явлений переноса.